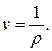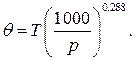Приближенное уравнение адиабатического процесса сухого воздуха или сухой адиабаты имеет вид (5 видео)

Содержание

Что такое адиабатический процесс? По какому закону происходят суходиабатические изменения температуры воздуха?
АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ
Адиабатические изменения температуры воздуха
Экология СПРАВОЧНИК
Информация
Адиабата сухая
💥 Видео

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Что такое адиабатический процесс? По какому закону происходят суходиабатические изменения температуры воздуха?

Адиабати́ческий, или адиаба́тный проце́сс— термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством.
Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит.
Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой.
Сухоадиабатический процесс

Адиабатическое изменение состояния сухого или ненасыщенного влажного воздуха. Температура и давление связаны при этом уравнением Пуассона, изменение температуры с изменением высоты перемещающегося воздуха при С. П. характеризуется сухоадиабатическим градиентом температуры.

Адиабатический подъем сухого воздуха ведет только к падению температуры в нем.При подъеме влажный насыщенный воздух охлаждается иначе, чем ненасыщенный, т. е. уже не по сухоадиабатическому закону.В сухом и ненасыщенном влажном воздухе при сухоадиабатическом процессе изменение температуры на единицу изменения высоты — величина постоянная (прямолинейная зависимость). Однако при влажноадиабатическом процессе изменение температуры на каждую единицу высоты — величина переменная. И линии изменения температуры в осях координат температура — высота — кривые, а не прямые. По мере увеличения высоты насыщающие количества водяного пара становятся все меньше и меньше, влажноадиабатический градиент приближается к сухо-адиабатическому градиенту, поэтому наклон влажных адиабат приближается к наклону сухих адиабат. По этой причине на графике влажные адиабаты обращены выпуклостью вверх.
При очень низких температурах, которые имеет воздух, поднимающийся в высоких слоях атмосферы, водяного пара в нем остается мало и выделение теплоты конденсации поэтому тоже незначительное. Падение температуры при адиабатическом подъеме в таком воздухе приближается к падению в сухом воздухе. Иначе говоря, влажноадиабатический градиент при низких температурах приближается по величине к сухоадиабатическому градиенту.
При опускании насыщенного воздуха процесс изменения температуры происходит по-разному в зависимости от того, остались ли в воздухе продукты конденсации (капли и кристаллы) или они уже целиком выпали из воздуха в виде осадков.
Если в воздухе нет продуктов конденсации, то как только он начнет опускаться и начнет расти температура, воздух становится ненасыщенным. Следовательно, изменение температуры пойдет по сухоадиабатическому закону, т. е. воздух, опускаясь, будет нагреваться на 1°С/100 м.
Если в воздухе сохранились продукты конденсации (капельки и кристаллы), образовавшиеся при подъеме, то при опускании и нагревании воздуха они будут постепенно испаряться. При этом часть внутренней энергии опускающегося воздуха затрачивается на испарение капелек и кристаллов, т. е. часть тепла воздушной массы переходит в скрытую теплоту парообразования, поэтому температура повышается меньше, чем при сухоадиабатическом опускании.

Как меняется температура в поднимающемся вертикально индивидуальном объеме сухого воздуха? Чему равен сухоадиабатический градиент температуры?

Расчеты показывают, что если сухой или ненасыщенный воздух поднимается без теплообмена с окружающей атмосферой, т. е. адиабатически, то температура его понижается на 1°С на каждые 100 м подъема. Эта величина называется сухоадиабатическим градиентом температуры. Начиная с уровня, на котором температура достигает значения точки росы, воздух становится насыщенным водяным паром Высота, на которой воздух при подъеме достигает насыщения, называется уровнем конденсации Дальнейший подъем воздуха сопровождается конденсацией водяного пара, при которой выделяется скрытая теплота ’конденсации, за счет чего температура будет падать медленнее, чем до начала конденсации. Понижение температуры в насыщенном воздухе на каждые 100 м подъема называется влажно-адиабатическим градиентом температуры.

Как меняется температура в поднимающемся вертикально индивидуальном объеме влажного воздуха? В чем принципиальное различие между адиабатическим подъемом сухого и влажного воздуха?

Если сухоадиабатический градиент — величина постоянная, то величина влажно-адиабатического зависит от температуры и давления. На высотах до 5—6 км влажно-адиабатический градиент в среднем равен 0,5— 0,6° С на 100 м. При опускании (нисходящем движении) как сухого, так и влажного воздуха температура повышается на 1°С на каждые 100 м. Воздух из-за этогоудаляется от состояния насыщения, и если это происходит в облаках, то капельки воды, из которых они состоят, испаряются Значит, облако распадается.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ

В атмосфере постоянно происходят перех од ы од них вид ов энергии в другие. Наиболее х арактерными являют ся переходы тепловой энергии в механическую и обратно, которые осуществляются при термодинамических процессах.

Адиабатическим процессом называется термодинамический процесс, при котором изменение температ ур ы в некотором объеме воздуха происх одит без теплообмена с окружающей средой. При адиабатических процессах расширение воздуха сопровожд ает ся его охлаждением, а сжатие — нагреванием. В атмосфере адиабатические процессы наблюдаются при вертикальных д вижениях воздуха.

При восходящих пот оках воздух , попадая из более плот ных слоев атмосферы в менее плотные, расширяет ся. На работу расширения трат ится внутр енняя тепловая энергия, вследствие чего поднимающ ийся воздух охлажд ается.

При д вижении вниз (нисх одящие пот оки) воздух попадает под большее давление и сжимает ся. Производ имая при эт ом работа внешних сил (д авление окр ужающей атмо сферы) переходит в тепловую энергию, поэтому опускающийся воздух нагревает ся.

Величина изменения температуры воздуха, в зависимости от изменения д авления,

определяется уравнением Пуассона

=ç ÷

где: Р0 и Т0 — начальные величины давления и т емперат уры;

Р и Т — давление и абсолютная температ ура массы воздуха при адиабат ическом изменении ее сост ояния.

Различают сухоадиабатические и влажноадиабат ические процессы. Сухоадиабат и- ческие процессы происходят в сухом или влажном, но ненасыщенном воздухе. Влажноадиабатические процессы — во влажном насыщ енном воздухе.

Количественной мерой изменения т емпературы сухого воздуха при адиабат ическом процессе являет ся сухоадиабатический градиент gα — изменение температуры в сухом или влажном ненасыщ енном воздухе при его подъеме или опускании на каждые 100 м высоты. Расчет показывает, что величина

g a = 0,98°С /100 м » 1°С /100 м = const .

При поднятии воздуха вверх на каждые 100м высоты происходит понижение его температ уры на 1°С, а при опускании воздуха вниз — повышение т емперат уры также на 1°С на 100 м высоты.

В воздухе, насыщ енном водяными парами, изменение температуры при подъеме

происходит по иному. Если вверх поднимается насыщенный воздух, то при понижении температуры за счет расширения, част ь вод яных паров конденсирует ся. В результате этого выделяется скрытая теплота конденсации (597 кал/г), кот орая существенно уменьшает охлаждение воздуха. Поэ тому насыщенный воздух при подъеме на 100 м охлаждается на величину меньш ую, чем 1°С. Эта величина называется влажноадиабатическим градиентом gвα .

Влажноадиабатический град иент величина непост оянная и зависит от температ уры и давления возд уха (табл. 5.1).

Таблица 5.1. Значения влажноадиабатического град иента ( °С/100 м)

Дав ление, гПа	Температура
-30°	-20°	-10°	0°	+10°	+20°	+30°
0,94	0,88	0,78	0,66	0,54	0,44	0,38
0,87	0,75	0,60	0,47	0,38	0,31	0,27

Чем вы ше температ ура в поднимающемся насыщенном воздухе, тем меньше величина влажноадиабатического градиента. Это объ ясняется тем, что при б олее высокой температуре в насыщенном воздухе содержится большое количест во водяного пара, при конденсации которого выделяется б ольшое количество скрытого т епла, в результате чего поднимающ ийся воздух охлаждается не так сильно. Если насыщ енный воздух имеет низкую т емпературу, то в нем содержит ся очень небольшое количест во водяного пара, в связи с чем происходит незначительное выделение скрыт ой теплоты в период его конд енсации, и величина охлаждения воздуха при его поднятии приближается к сухоадиабатическому градиенту. С уменьшением д авл ения (при одной и т ой же температуре) влажноадиабатический градиент

уменьшается, так как воздух ст ановит ся менее плот ным и освобождающ аяся скрыт ая т еплот а конденсации идет на нагревание меньшей массы воздуха. В среднем

gвa =0,5°С /100 м . С высотой влажноадиабатический градиент увеличивается, и его

величина приближает ся к сухоадиабатическому градиент у.

При опускании насыщенного воздуха происход ит его адиабатическое нагревание, и он удаляется от состояния насыщ ения (т.е. ст ановится ненасыщенным). Следовательно, опускающийся воздух всегда б уд ет нагреваться по сухоадиабатическому закону, т.е. на 1°С на каждые 100 м.

Изменение т емпературы при адиабатических процессах можно изобразить графически при помощ и линий, называемых адиабатами.

Линия, которая показывает изменение т емпературы в поднимающемся или

опускающемся сух ом воздухе, называется сухой адиабатой (рис. 5.9).

Рис. 5.9. Сухие адиабаты Рис. 5.10. Влажные адиабаты

Формула изменения температуры при сухоадиабат ическом процессе представляет собой уравнение прямой линии

Если откладывать на осях координат в одинаковом масштабе температуру в 1°С и высоту

100 м, то прямая линия — сухая ад иабата — будет наклонена к оси т емператур под углом 45°.

Линия, характеризующ ая изменение температ уры в поднимающемся насыщ енном воздухе, называется влажной адиабатой (рис. 5.10). Влажные адиаб аты, в отличие от сухих, являются изогнутыми линиями, пот ому что gвa величина непост оянная, при поднят ии насы щенного возд уха gвa увеличивается, приближаясь к ga .

Адиабатические изменения т емпературы могут наблюдаться и непосредст венно у земной поверхности при изменении давления. Повыш ение или понижение д авления на 1 гПа (при давлении Р » 1000 гПа) вызывает соот ветст вующее повышение или понижение т емпературы на 0,08°С .

Видео:Адиабатный процесс. 10 класс.Скачать

Адиабатические изменения температуры воздуха

Выше мы рассмотрели процессы теплообмена атмосферы с подстилающей поверхностью, оказывающие существенное влияние на тепловой режим приземной атмосферы. Важную роль в атмосфере играют также адиабатические изменения температуры воздуха.

Адиабати́ческий [от греч. adiabatos – непереходимый] – происходящий без притока и отдачи тепла, т.е. без теплового взаимодействия с окружающей средой. Строго адиабатических процессов в атмосфере быть не может:тепловое влияние окружающей среды всегда имеет место. Однако если перемещение некоторой массы газа в окружающем «спокойном» воздухе протекает быстро, и теплообмен ее с окружающим воздухом мал (молекулярная теплопроводность воздуха очень мала), то изменение температуры газа близко к адиабатическому.

В дальнейшем полагаем, что теплота фазовых превращений воды (конденсации или испарения) не играют роли, т.е. рассматриваем сухой или ненасыщенный паром воздух. В этом случае процесс называется «сухоадиабатическим».

Рассмотрим единицу массы газа плотностью p. Объем единицы массы газа – удельный объем – равен

Пусть Q – тепловой поток между рассматриваемой массой газа и окружающим воздухом. Под массой газа (рис. 3.2) понимаем некоторую массу воздуха, имеющего какие-либо отличные свойства. Например, тепловые выбросы из заводской трубы. Или, другой пример: масса теплого воздуха, поднимающаяся от разогретого участка земной поверхности.

Приближенное уравнение адиабатического процесса сухого воздуха или сухой адиабаты имеет вид

Рис. 3.2. Обмен энергией между массой газа и окружающим воздухом. Q – поток тепла между массой газа и окружаемым воздухом; А – работа расширения или сжатия, совершаемая массой газа

Согласно первому закону термодинамики, количество теплоты (Q), получаемой или отдаваемой рассматриваемой массой газа, расходуется:

1) на изменение его внутренней энергии;

2) на совершение работы, связанной с расширением (работа против внешних сил давления) или сжатием (работа со стороны внешних сил давления) газа.

Уравнение первого закона термодинамики имеет вид:

где dQ – элементарное количество теплоты, dU – приращение внутренней энергии, dA – элементарная работа расширения или сжатия.

Изменение внутренней энергии единицы массы газа выражается в повышении или понижении его абсолютной температуры (Т):

, (3.17)

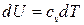
где 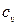– теплоемкость при постоянном объеме.

Для определения работы расширения (сжатия) рассмотрим элементарный объем газа в форме куба c площадью боковых граней S. Пусть в результате расширения (сжатия) длины ребер куба изменились на величину dx, dy, dz. Сила давления газа на любую грань равна произведению давления газа p на площадь грани (F=pS). Работа сил давления равна произведению силы на путь. Если общее изменение длин ребер составляет dx, dy, dz, то каждая из граней переместилась на расстояния: вдоль соответствующих осей координат на 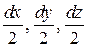. Всего гра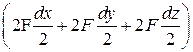ней шесть, следовательно, выражение для работы расширения (сжатия), производимой силой F, одинаковой для каждой пары симметричных граней, примет вид:

А= . (3.18)

Подставив в (3.18) выражение для силы (F=pS) и вынося давление p за скобки, получим

где dv= Sdx+Sdy+Sdz – элементарное приращение рассматриваемого объема газа в результате его расширения (знак +), или сжатия (знак –).

С учетом (3.17) и (3.19) уравнение первого начала термодинамики (3.16) для нашей задачи получает вид:

. (3.20)

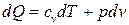
Учтем, что для адиабатического процесса, условием которого является отсутствие теплообмена рассматриваемой массы газа с окружающим «спокойным» воздухом (dQ=0):

=0. (3.21)

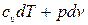
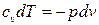
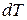
Последнюю формулу можно переписать: , откуда следует, что при расширении объема рассматриваемой массы воздуха (dv>0) внутренняя энергия, и, следовательно, температура уменьшаются ( 0, то градиент γ отрицательный. Такая трактовка (назовем ее традиционной) принята, например, в [84]. Ниже мы придерживаемся традиционной трактовки.

Обратим внимание читателя, что в некоторых работах величина градиента определяется как γ = Δt°/100 м (знак минус опущен). В этом случае, если температура падает с высотой, то градиент γ отрицательный, а если она увеличивается с высотой, то градиент γ положительный.

Теория Пуассона позволяет рассчитать, как изменится температура массы сухого воздуха при ее адиабатическом подъеме или опускании на определенную высоту. С этой целью совместно решаются уравнение адиабатического процесса (3.21), уравнение состояния газа Клапейрона – Менделеева (1.1) и дифференциальное уравнение статики атмосферы (1.12).

Опуская математические преобразования, получим выражение для сухоадиабатического градиента температуры

0.0098 о /м,

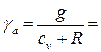
или 0.98 о /100 м (с округлением 1 о /100 м). Следовательно, при адиабатическом подъеме индивидуальной массы сухого или ненасыщенного воздуха температура в ней падает примерно на один градус на каждые 100 м подъема, а при адиабатическом опускании – растет на ту же величину.

Следует различать сухоадиабатический градиент температуры воздуха γ_а = 1°/ 100 м, возникающий при адиабатических движениях отдельных масс воздуха, и градиент температуры γ окружающего спокойного воздуха. Напомним, что в тропосфере температура уменьшается с ростом высоты в среднем на 0,6° на каждые 100 м, т.е. γ = 0.6 о /100 м. На самом деле γ изменяется во времени и пространстве, о чем будет сказано ниже.

Влажноадиабатические изменения температуры. При адиабатическом подъеме происходит падение атмосферного давления и удельный объем газа увеличивается, а его температура, как показано выше, падает. Если газ содержит водяной пар, то на некоторой высоте наступает состояние насыщения и начинается конденсация. Эта высота называется уровнем конденсации. При конденсации выделяется теплота (2.512×10 3 Дж. на 1 грамм образовавшейся воды). Выделение этой теплоты замедляет падение температуры газа при его дальнейшем подъеме.

Если сухоадиабатический градиент температуры (γ_а) равен 1°/100 м, то влажноадиабатический градиент (γ_в) окажется меньше этой величины. Разница (γ_а – γ_в) увеличивается при увеличении количества водяного пара в состоянии насыщения, которое, в свою очередь, зависит от температуры и давления. Так, при давлении 1000 мб влажноадиабатический градиент температуры равен:

при температуре – 20°С γ_в = 0.88°/100 м,

при температуре +20°С γ_в = 0.44 °/100 м, т.е. окажется более чем в два раза меньше сухоадиабатического градиента температуры (γ_а). Этот результат объясняется просто: чем ниже температура воздуха, тем меньше влажность воздуха в состоянии насыщения (табл. 4.1) и, следовательно, меньше теплоты выделяется при конденсации.

Если рассматриваемый объем газа опускается, то температура его повышается, следовательно, количество содержащегося в нем пара окажется меньше, чем в состоянии насыщения. В этом случае теплота конденсации не выделяется, и градиент температуры приближается к сухоадиабатическому (1°/100 м), т.е. температура повышается каждые 100 м спуска на 1°.

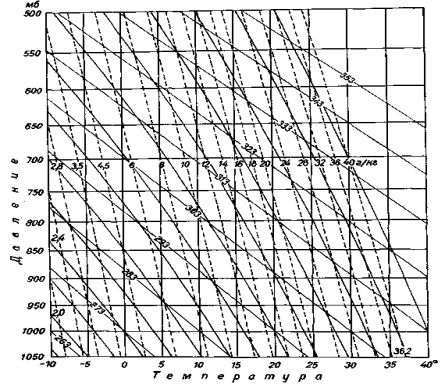
Можно, используя уравнение сухоадиабатического закона (3.22), построить график связи между давлением и температурой при адиабатическом процессе в вертикально движущемся воздухе (адиабатная диаграмма, рис. 3.3). Кривая, графически представляющая изменение температуры, называется сухой адиабатой, если конденсация отсутствует, и влажной адиабатой – при наличии конденсации.

Рис. 3.3. Адиабатная диаграмма.

Сплошные линии с большим углом наклона – сухие адиабаты, с меньшим углом наклона – влажные адиабаты, прерывистые линии – изолинии удельной влажности для состояния насыщения

С помощью адиабатной диаграммы можно графически определить изменение температуры при адиабатических процессах. Зная температуру Т₀ и давление р₀ в начальный момент, найдем на диаграмме соответствующую точку. Если воздух меняет свое состояние по сухоадиабатическому закону, перемещаемся по сухой адиабате до тех пор, пока не достигнем ординаты с давлением р. В этой точке определим по диаграмме, каково будет значение температуры воздуха Т.

Если при некотором давлении р’ воздух стал насыщенным, нужно дальше прослеживать его состояние, но следуя уже по влажной адиабате, начиная с точки, соответствующей давлению р’.

На адиабатной диаграмме у сухих адиабат подписаны так называемые «потенциальные температуры θ» в градусах Кельвина. Они равны температурам сухоадиабатического процесса, соответствующим стандартному давлению 1000 мб. Например, сухая адиабата с надписанной температурой 273 о пересекает ординату с давлением 1000 мб при температуре 0 о С (или 273 о К). Иными словами, если с какой-то высоты в атмосфере с давлением р и температурой Т, воздух сухоадиабатически опускается на уровень, где давление равно 1000 мб, то температура его на этом уровне окажется равной потенциальной (θ о К). Ее определяют исходя из уравнения Пуассона (3.22)

Потенциальную температуру можно также определить, если на заданной высоте z известна температура воздуха Т. Полагаем, что на уровне моря давление близко или равно стандартному (1000 мб). При адиабатическом опускании градиент температуры γ_а равен 1 о , т.е. температура увеличивается примерно 1 о на каждые 100 м спуска. Следовательно, потенциальная температура при опускании воздуха с высоты z на уровень моря окажется равной

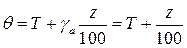
С помощью потенциальной температуры удобно сравнивать тепловое состояние масс воздуха, находящихся на разных высотах над уровнем моря (т. е. при разных давлениях), поскольку, вычисляя потенциальную температуру этих масс, мы как бы «опускаем» их на один высотный уровень.

Дата добавления: 2015-09-07 ; просмотров: 9351 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Изопроцессы, Адиабатный процесс.Скачать

Экология СПРАВОЧНИК

Видео:Адиабатическое охлаждение.Скачать

Информация

Добавить в ЗАКЛАДКИ

Поделиться:

Видео:Физика 10 класс. Адиабатный процесс.Скачать

Адиабата сухая

Кривая, изображающая связь между двумя характеристиками состояния атмосферного воздуха при адиабатическом процессе. Основные характеристики состояния при этом — давление и удельный объем воздуха; но адиабаты строятся также и для других переменных, функционально связанных с указанными основными, напр., для температуры и давления, для температуры и потенциальной температуры. Часто строят адиабаты для переменных температура — высота, поскольку при изменении высоты индивидуальной массы воздуха меняется и ее давление. См. сухая адиабата, влажная адиабата, сублимационная адиабата.[ . ]

Сплошные линии с большим углом наклона — сухие адиабаты, с меньшим — влажные адиабаты, прерывистые линии — изолинии удельной влажности для состояния насыщения.[ . ]

П. Т. воздуха при сухоадиабатическом процессе не меняется; сухие адиабаты на адиабатной диаграмме являются также линиями равной П. Т. Для воздуха, находящегося на высоте г над уровнем моря, П. Т. легко получить приближенно, учитывая, что на каждые 100 м опускания температура при сухоадиабатическом процессе растет на 1°. Тогда, принимая, что на уровне моря давление стандартное 0 = Т + 2, где г — высота в сотнях метров.[ . ]

Аэрологическая диаграмма с координатами Т и 1д р. Изоплеты на диаграмме — сухие и влажные адиабаты и линии равной удельной влажности для насыщения.[ . ]

Аэрологическая диаграмма с координатами х = т (где т — отношение смеси) и у — 1£0с (где ©с — парциальная потенциальная температура сухого воздуха). На диаграмме нанесены еще влажные адиабаты, а также изобары и изотермы для состояния насыщения.[ . ]

Переработанная диаграмма Герца, на которой по осям координат нанесены в линейной шкале температура и высота, а на бланке построены сухие и влажные адиабаты и изолинии максимальной удельной влажности.[ . ]

В плоскости х, у значения потенциальной температуры представляются в виде пучка прямых, проходящих через начало координат Т= 0 и р = 0. Эти прямые называют сухими адиабатами.[ . ]

КРИВАЯ СОСТОЯНИЯ. Кривая на адиабатной (аэрологической) диаграмме, графически представляющая адиабатические изменения состояния вертикально смещающейся воздушной частицы. Если воздух сухой, кривая состояния является сухой адиабатой, проходящей через точку, координатами которой являются характеристики состояния воздуха на исходной высоте; если воздух влажный, кривая состояния до уровня конденсации является сухой адиабатой, а начиная с этого уровня совпадает с влажной адиабатой.[ . ]

Значения L0 прогнозируются для дневного и утреннего времени. В первом случае в соответствии со сказанным выше значение Lq соответствует уровню пересечения кривых стратификации утреннего зондирования и сухой адиабаты, проведенной через точку ожидаемого приземного максимума дневной температуры. Во втором случае для определения Ьо сухая адиабата проводится через точку, соответствующую Гшт-Ь 6 7г, где Tmin — минимальная температура у земной поверхности за городом, а 6ТГ — разность температуры в городе и его окрестностях, в среднем принимаемая равной 5°С. В утренние часы значение Lq существенно меньше, чем днем, а выбросы от автомашин в это время наибольшие. Поэтому утром следует ожидать и наибольших значений концентрации первичных примесей, непосредственно содержащихся в автомобильных выхлопах. Вскоре после полудня высота L0 принимает максимальные значения, а концентрации первичных примесей становятся минимальными. Однако в это время достигает максимума интенсивность образования вторичных примесей в процессе фотохимических реакций, происходящих под влиянием солнечной радиации.[ . ]

ДИАГРАММА ГЕРЦА. Пер вая адиабатная диаграмма, построенная Г. Герцом в 1884 г.; прообраз последующих адиабатных (аэрологических) диаграмм. По осям координат нанесены в логарифмической шкале давление и температуры воздуха; на графике построены изолинии максимальной удельной влажности, сухие адиабаты и влажные адиабаты для стадий дождя и снега (т. е. конденсационные при положительных температурах и сублимационные при отрицательных температурах), линия плотности влажного воздуха и шкала высот.[ . ]

Потенциальная температура, в отличие от молекулярной температуры Т, при сухоадиабатических перемещениях одной и той же воздушной частицы остается постоянной. Если в процессе перемещения воздушной массы ее потенциальная температура изменилась, то наблюдается приток или отток тепла. Сухая адиабата является линией равного значения потенциальной температуры.[ . ]

АДИАБАТНАЯ ДИАГРАММА. Диаграмма с (обычно) прямоугольными осями координат, по которым отложены характеристики состояния воздуха: напр., удельный объем и давление или температура и давление, или температура и потенциальная температура и т. д. Давление воздуха можно заменить высотой. На А. Д. нанесены семейства сухих и влажных адиабат, т. е. кривых, графически представляющих изменение состояния воздуха при сухоадиабатическом и влажноадиабатическом процессах; наносятся также кривые, представляющие собой зависимость удельной влажности или упругости пара для состояния насыщения от основных характеристик, отложенных по осям диаграммы; иногда добавляются изолинии других функций основных характеристик.[ . ]

Высота слоя перемешивания. Высоту слоя перемешивания (ВСП) определяли с помощью аэрологической диаграммы, используя ежедневные данные радиозондирования и метеорологических наблюдений за максимальной температурой воздуха. На аэрологической диаграмме находили точку пересечения кривой вертикального распределения температуры воздуха в ночной срок с прямой, проходящей по сухой адиабате через начальную точку максимума наземной температуры воздуха. Проекцию данной точки на ось ординат принимали за максимальную за сутки ВСП.[ . ]

Зондирование с помощью радиозондов можно представить на таких диаграммах линиями, показывающими, как температура Т и, скажем, температура точки росы Тd меняются в зависимости от давления. Диаграмму (которую тогда можно назвать аэрологической диаграммой) можно использовать для выводов относительно устойчивости, результатов подъема образцов воздуха и т. д. Один пример (Кейптаун, Южная Африка) показан жирными линиями на рис. 3.6, а. Сразу ясно, что в нижнем километре воздух ближе к насыщению, чем воздух над ним, так как в нем разность между Т и Т,i относительно мала. Свойства устойчивости можно оценить, сравнивая наклон температурной кривой, полученный при зондировании, с наклоном сухой и влажной адиабат. В данном примере воздух около земли условно устойчив, так как наблюдаемый наклон — промежуточный между наклонами этих двух адиабат. Нижний километр относительно влажного воздуха перекрывается слоем инверсии, где Т растет с высотой (до уровня 830 мбар); на более высоких уровнях воздух сухой. Он настолько сух, что только наклон относительно сухой адиабаты является показательным и свидетельствует об устойчивости (0 растет с высотой).[ . ]

Другой способ прогноза потенциала, который широко применяется в США, основывается главным образом на учете устойчивости нижнего слоя атмосферы и скорости переноса воздуха. Принимается, что необходимым условием значительного скопления примесей в городском воздухе при заданных выбросах является формирование ситуаций застоя воздуха (устойчивая стратификация, слабый ветер, отсутствие осадков). Обычно указанное сочетание наблюдается в стационарных антициклонах. Количественные критерии для определения застоя воздуха следующие: .средняя скорость ветра в нижнем 1,5-километровом слое не должна превышать 10 м/с; понижение температуры за 12 ч до утреннего срока наблюдений не г0 периодов — -должно превышать 5° С (этим , м кривая иратификаци;; 2 „ сухая условием отсеиваются случаи адиабата, с явно выраженной адвекцией холода); отсутствие осадков. В дальнейшем возможность возникновения опасного загрязнения воздуха рассматривается только в выделенных областях застоя.[ . ]