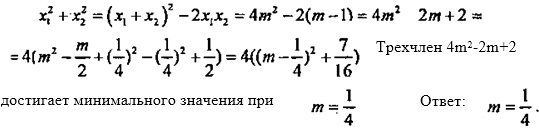При каком значении параметра а сумма квадратов корней уравнения минимальна

1) При каком значении m сумма квадратов корней
уравнения х 2 + (2 — m)х — m — 3 = 0 минимальна?

2) При каком значении m сумма квадратов корней
уравнения х 2 + 2mх + m — 1 = 0 минимальна?

(1) х 2 +(2-m)х-m-3 = 0. По теореме, обратной теореме Виета:
x 2 ₁+x 2 ₂= (x₁ + х₂) 2 -2х₁х₂ = (m-2) 2 -2(-m -3) —
= m 2 -4m+4+2m+6 = m 2 -2m+10 = m 2 -2m+1+9 = (m-1) 2 +9
Наименьшее значение трехчлен m 2 -2m+10 достигает при m = 1.
Ответ: m = 1.

(2) х 2 +2mх+m-1 = 0. По теореме, обратной теореме Виета:

Видео:При каких значениях а сумма квадратов корней уравнения x² + ax + a - 2 = 0 минимальна?Скачать

При каком значении параметра А сумма квадратов корней уравнения является наименьшей?

Математика | 10 — 11 классы

При каком значении параметра А сумма квадратов корней уравнения является наименьшей?

X ^ 2 + ax + a — 2 = 0.

При а = 0 Мне так кажется.

Видео:#67. Сумма квадратов корней в уравнении с параметром!Скачать

При каком наименьшем целом значении параметра а уравнение х ^ 4 — 8x ^ 2 — a = 0 имеет ровно 4 корня?

При каком наименьшем целом значении параметра а уравнение х ^ 4 — 8x ^ 2 — a = 0 имеет ровно 4 корня?

Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Найти значение параметра m , при котором сумма кубов действительных корней уравнения x ^ 2 + (m — 1) * x + (m ^ 2) / 3 = 0 будет наименьшей?

Найти значение параметра m , при котором сумма кубов действительных корней уравнения x ^ 2 + (m — 1) * x + (m ^ 2) / 3 = 0 будет наименьшей.

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

При каких значениях параметра а уравнение а(х(в квадрате) — х + 1) = 3х + 5 имеет два различных действительных корня?

При каких значениях параметра а уравнение а(х(в квадрате) — х + 1) = 3х + 5 имеет два различных действительных корня.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

При каких значениях параметра α уравнение имеет два различных корня?

При каких значениях параметра α уравнение имеет два различных корня.

Видео:Метод выделения полного квадрата. 8 класс.Скачать

Срочно нужно решить?

Срочно нужно решить!

При каком значении а сумма квадратов корней уравнения х ^ 2 + ax + a — 2 = 0 принимает наименьшее значение?

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

При каких значениях параметра а корни уравнения образуют арифметическую прогрессию?

При каких значениях параметра а корни уравнения образуют арифметическую прогрессию.

Видео:Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

1)X ^ 2 — 2a(x — 1) — 1 = 0 при каких значениях a сумма корней уравнения равна сумме квадратов его корней?

1)X ^ 2 — 2a(x — 1) — 1 = 0 при каких значениях a сумма корней уравнения равна сумме квадратов его корней?

2) x ^ 2 — 2x + a = 0 При каких значениях параметра уравнения имеет действительные корень, что 7X1 — 4X2 = 47?

Видео:Не решая квадратное уравнение, найдите сумму кубов его корнейСкачать

При каких значениях параметра m уравнение (во вложениях) имеет бесконечно много корней?

При каких значениях параметра m уравнение (во вложениях) имеет бесконечно много корней.

Видео:Что Такое Параметр? Параметр с Нуля + ДЗ (Задание 18 ЕГЭ 2024 Математика Профиль)Скачать

Найдите значение параметра m при котором сумма квадратов действительных корней уравнения x ^ 2 + 2(10m–1)x + 4m + 1 = 0 будет наименьшей?

Найдите значение параметра m при котором сумма квадратов действительных корней уравнения x ^ 2 + 2(10m–1)x + 4m + 1 = 0 будет наименьшей.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

При каком значении параметра a сумма квадратов корней уравнения x ^ 2 + (2a — 5) * x + (a ^ 2 — 5a + 6) = 0 минимальна?

При каком значении параметра a сумма квадратов корней уравнения x ^ 2 + (2a — 5) * x + (a ^ 2 — 5a + 6) = 0 минимальна?

Вы находитесь на странице вопроса При каком значении параметра А сумма квадратов корней уравнения является наименьшей? из категории Математика. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Видео:Найти значение суммы и произведения корней квадратного уравненияСкачать

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

📽️ Видео

Уравнения с параметром. Алгебра, 8 классСкачать

Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать

✓ Пять способов решить задачу с параметром | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Сумма квадратов | Ботай со мной #061 | Борис Трушин |Скачать

Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать

✓ Параметры в ЕГЭ? Это не страшно! | Математика. Задание 17 | #ТрушинLive​​ #036 | Борис ТрушинСкачать

ЗАДАЧА О СУММЕ КВАДРАТОВСкачать

Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать