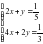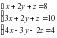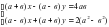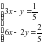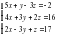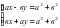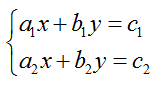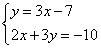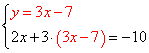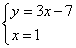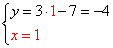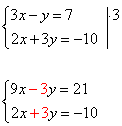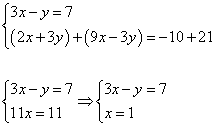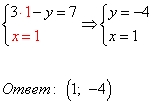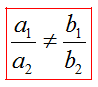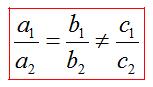- Практическая работа по теме “Решение систем уравнений в среде Microsoft Excel”
- Практическая работа по теме “Стандартные функции Microsoft Excel”
- Практическая работа по теме: «Решение систем линейных уравнений»
- Просмотр содержимого документа «Практическая работа по теме: «Решение систем линейных уравнений»»
- Практическая работа «Решение систем уравнений в Excel» методическая разработка (информатика и икт, 9 класс) по теме
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 🌟 Видео
Практическая работа по теме “Решение систем уравнений в среде Microsoft Excel”
Цель работы:
- освоить основные приемы работы с Мастером диаграмм в MS Excel;
- научиться решать системы уравнений с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
Задача 1. Решить графически систему уравнений
Основное задание. Найти решение системы уравнений
1. Заполните таблицу, как показано на рисунке 1:
2. Выделите блок В2:В17. Постройте диаграмму – график, как показано на рис.2.
3. ПКМ вызовите вкладку Исходные данные. Выполните Ряд, Добавить, Значения. ЛКМ выделите блок С2 : С17.
4. В окне Подписи оси Х занесите значения x, выделив блок А2 : А17. Завершите построение диаграммы и найдите решение системы. Решение запишите в тетрадь. (Рис. 3)
Дополнительное задание. Оформите решение.
1. Выбрав вкладку Параметры диаграммы ПКМ, добавить основные линии сетки по осям OX и OY.
2. В “Исходных данных” во вкладке Ряд добавить имена рядов: 

3. Щелкнув ПКМ по оси OX, выбрать меню Формат оси, Шкала; установить соответствующие значения. (Рис.4)
4. Щелкнув ПКМ по оси OY, установить цену основных делений 1 и во вкладке Шрифт уменьшить размер шрифта.
5. Щелкнув ПКМ, выбрать Формат области построения, во вкладке Вид поставить флажок Заливка прозрачная.
6. Сравните полученный результат с образцом, представленным на рисунке 5.
Задача 2. Решить графически систему уравнений
Практическая работа по теме “Стандартные функции Microsoft Excel”
Цель работы:
- освоить основные приемы работы со стандартными функциями в MS Excel;
- научиться решать задачи табулирования функции с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
Функции
Для записи формул в электронных таблицах можно использовать стандартные функции. Всё множество встроенных функций табличного процессора делится на несколько групп: математические, статистические, функции даты и времени и т.д. В различных табличных процессорах наборы стандартных функций различаются.
Таблица некоторых стандартных функций Excel
| SIN() | синус |
| COS() | косинус |
| TAN() | тангенс |
| КОРЕНЬ()(SQRT) | корень |
| ABS() | модуль |
| СУММА() | сумма |
| СРЗНАЧ()(AVERAGE) | среднее значение |
| МАКС()(MAX) | максимум |
| МИН(MIN) | минимум |
Задача 1. На отрезке [0;1] вычислить значения функции 
1. Заполните таблицу, как показано ниже на рисунках 1 и 2.
2. Скопируйте формулу из ячейки А4 в ячейки А5 : А8, а формулу из ячейки В3 в ячейки В4 : В8.
При копировании абсолютный адрес $B$1, содержащий значение шага табуляции, не будет изменяться.
3. Загрузите режим отображения формул: Сервис/параметры/вид/формулы.
В режиме отображения формул таблица будет выглядеть так, как показано на рисунке 3:
4. Отмените режим отображения формул. В режиме отображения значений таблица будет выглядеть так, как показано на рисунке 4:
Задачи для самостоятельной работы:
Задача 2. На отрезке [1,2; 2] вычислить значения функции 
Задача 3. На отрезке [2;4] вычислить значения функции 
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Практическая работа по теме: «Решение систем линейных уравнений»
Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера.
Просмотр содержимого документа
«Практическая работа по теме: «Решение систем линейных уравнений»»
Краевое государственное образовательное учреждение среднего профессионального образования «Хабаровский судостроительный колледж»
Специальность: 15.02.08 «Технология машиностроения»
Дисциплина: ЕН.01. «Математика», курс -1
Преподаватель — Михайлова М.Б.
Тема занятия: «Практическая работа: «Решение систем линейных уравнений»
Практическая работа по теме:
«Решение систем линейных уравнений»
Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера.
Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:
а) 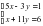
Решите систему уравнений по формулам Крамера:
Решите систему уравнений по формулам Крамера:
4. При каком значении а система 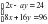
Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:
а) 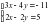
Решите систему уравнений по формулам Крамера:
Решите систему уравнений по формулам Крамера:
При каком значении а система 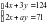
Методические рекомендации для выполнения
практической работы по теме:
«Решение систем линейных уравнений»
Системы линейных уравнений
Решение системы линейных уравнений способом подстановки
Решение системы линейных уравнений способом сложения
Графическое решение системы линейных уравнений
График линейной функции
1. Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
Система уравнений такого вида, где a, b, c – числа, а x, y — переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
2. Решение системы линейных уравнений способом подстановки
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.
3. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 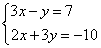
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
4. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
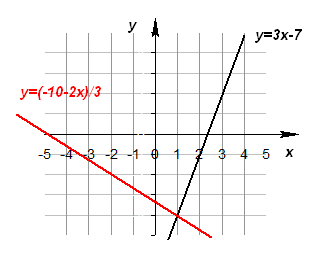
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система (1)
1) Если , то система (1) имеет единственное решение.
2) Если ,, то система (1) решений не имеет.
В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.
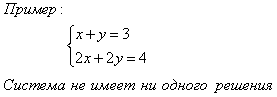
3) Если , то система (1) имеет бесконечное множество решений.
В этом случае прямые совпадают друг с другом.
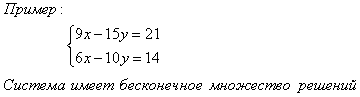
II.Решение систем линейных уравнений по формулам Крамера
Система двух линейных уравнений с двумя переменными
Определитель системы уравнений.
Система трех линейных уравнений с тремя переменными
1.Решение систем линейных уравнений по формулам Крамера
Габриель Крамер (1704–1752) швейцарский математик.
Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, то есть ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель системы не равнялся .
Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
2.Система из двух уравнений с двумя неизвестными
решается с помощью формул Крамера:
При решении системы возможны три случая:
1. Определитель системы . Тогда система имеет единственное решение, определяемое формулами Крамера.
2. Определитель системы . Если при этом хотя бы один из определителей и не равен нулю, то система не имеет решений.
3. Если , и , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
П р и м е р 1. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители ,
Система имеет единственное решение
П р и м е р 2. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители , . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
Ответ: нет решений.
П р и м е р 3. Решить систему уравнений
Решение. Вычислим определитель системы , и дополнительные определители .
Так как , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на ).
Система сводится к одному уравнению и имеет бесчисленное множество решений, каждое из которых вычисляется по формуле: , где числовые значения задаются произвольно и вычисляются соответствующие значения .
Ответ: – общее решение данной системы, а решения – частные.
3.Система из трех уравнений с тремя неизвестными
При решении системы из трех уравнений с тремя неизвестными возможны три случая:
1. Определитель системы . Система имеет единственное решение, определяемое формулами Крамера ,
2. Определитель системы равен нулю, . Если при этом хотя бы один из определителей , не равен нулю, то система несовместна, решений не имеет.
3. Если и , то система имеет бесчисленное множество решений.
П р и м е р 4. Решить систему уравнений
Решение. Вычислим определитель системы и дополнительные определители
Видео:Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать

Практическая работа «Решение систем уравнений в Excel»
методическая разработка (информатика и икт, 9 класс) по теме
Практическая работа «Решение систем уравнений в Excel»
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| prakticheskaya_rabota.doc | 305 КБ |
Видео:Графический способ решения систем уравнений | Алгебра 9 класс #18 | ИнфоурокСкачать

Предварительный просмотр:
1.Заполняем строку х:
2.Заполняем строку У1
-в ячейку В2 записываем , нажимаем на ENTER
-выделяем диапазон B2:H2
Правка- заполнить- вправо
3.Заполняем строку У2
-в ячейку В3 записываем =B3-1 , нажимаем на ENTER
-выделяем диапазон B3:H3
-Правка- заполнить- вправо
Видео:Решение системы уравнений графическим методомСкачать

По теме: методические разработки, презентации и конспекты
Занятие «Графический способ решения уравнений и систем уравнений в среде Microsoft Excel «
Занятие в среде Microsoft Excel. Графическое решение уравнения и системы уравнений с помощью Мастера диаграмм.
Построение диаграмм и графиков. Решение систем уравнений графическим способом в MS Excel»
Построение диаграмм и графиков. Решение систем уравнений графическим способом в MS Excel».
Разработка интегрированного урока математика и информатика по теме «Графический способ решения систем уравнений в среде Microsoft Excel»
Разработка интегрированного урока математика и информатика по теме «Графический способ решения систем уравнений в среде Microsoft Excel».
Графический способ решения систем уравнений в Excel
Урок закрепления изученного материала и объяснения нового.
Построение диаграмм и графиков. Решение систем уравнений графическим способом в MS Excel
Урок закрепления изученного материала и объяснения нового.
Презентации по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложения для решения систем уравнений» .
Презентации проедполагает использование при проведении онлайн урока по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложени.
Конспект урока на тему «Графический способ решения систем уравнений в Excel»
Графический способ решения систем уравнений в Excel.
🌟 Видео
Решение системы линейных уравнений графическим способом. 7 классСкачать

Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Графический метод решения систем линейных уравнений 7 классСкачать

Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Урок по теме ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ 7 КЛАСССкачать

Решение систем уравнений графическим способомСкачать

Практическая работа "Решение задач линейного программирования графическим методом".Скачать

ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ. Видеоурок | АЛГЕБРА 9 классСкачать

Графический метод решения уравнений 8 классСкачать

Решение систем уравнений графическим способомСкачать

Решение систем линейных уравнений графическим способом ( 7 класс)Скачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Решение систем уравнений графическим способомСкачать

Графический способ решения систем уравненийСкачать