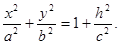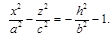Напомним, что многочленом степени одной переменной называется выражение вида
где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .
Многочленом трех переменных называется выражение вида
называется степенью многочлена трёх переменных.
Алгебраической поверхностью называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где — многочлен трех переменных .
Уравнение вида (4.11) называется алгебраическим уравнением с тремя неизвестными. Степенью уравнения (4.11) называется степень многочлена . Одна и та же поверхность может быть задана уравнением вида (4.11) с многочленами разных степеней. Порядком алгебраической поверхности называется наименьшая из степеней этих многочленов.
Всякую неалгебраическую поверхность называют трансцендентной.
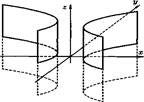
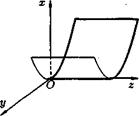
В примере 4.1,а,б,в,г — поверхности алгебраические: а — первого порядка. б,в,г — второго порядка. Примером трансцендентной поверхности служит цилиндрическая поверхность (см. рисунок), образующие которой, параллельные оси , пересекают координатную плоскость в точках синусоиды . Эту линию нельзя задать уравнением вида (4.11).
- Теорема (4.1) об инвариантности порядка алгебраической поверхности
- Поверхности второго порядка: их виды, уравнения, примеры
- Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
- Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
- Эллипсоид
- Мнимый эллипсоид
- Мнимый конус
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Конус
- Эллиптический параболоид
- Гиперболический параболоид
- Эллиптический цилиндр
- Мнимый эллиптический цилиндр
- Мнимые пересекающиеся плоскости
- Гиперболический цилиндр
- Пересекающиеся плоскости
- Параболический цилиндр
- Параллельные плоскости
- Мнимые параллельные плоскости
- Совпадающие плоскости
- Решение примеров на определение вида поверхности второго порядка
- Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
- Лекция 12. Уравнение поверхности и кривой в пространстве
- 🌟 Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Теорема (4.1) об инвариантности порядка алгебраической поверхности
Если в некоторой аффинной системе координат в пространстве поверхность задана уравнением (4.11), то и в любой другой аффинной системе координат эта поверхность задается уравнением того же вида (4.11) и той же степени. Другими словами, порядок алгебраической поверхности является инвариантом (остается неизменным в любой аффинной системе координат).
Теорема доказывается аналогично теореме 3.1.
В аналитической геометрии в пространстве изучаются:
– алгебраические поверхности первого порядка , описываемые алгебраическим уравнением первой степени с тремя неизвестными
– алгебраические поверхности второго порядка , описываемые алгебраическим уравнением второй степени с тремя неизвестными
1. Теорема 4.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных
где , степень многочлена не изменяется.
2. Алгебраическое уравнение (4.11) может не иметь действительных решений. Например, в пространстве нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теореме алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (4.11) вида , где задает некоторую алгебраическую поверхность в трехмерном комплексном пространстве (см. пункт 2 замечаний 2.9). Если все точки этой поверхности вещественные (действительные), т.е. а то поверхность называют вещественной (действительной). В противном случае поверхность называют мнимой.
3. Алгебраическими неравенствами с тремя неизвестными называются неравенства вида
где — многочлен трех переменных . Степенью алгебраического неравенства называется степень многочлена .
4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.
5. Многочлен второй степени
называется также квадратичной функцией трех переменных; многочлен
называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.
6. Квадратичную функцию (см. пункт 5) можно записать:
а) в матричном виде
где — матрица квадратичной функции; — расширенный (дополненный единицей) столбец переменных;
б) выделяя квадратичную и линейную части:
где — матрица квадратичной формы, — столбец коэффициентов линейной формы, — столбец переменных.
Матрицы и называются также матрицами малой и большой квадратичных форм квадратичной функции .
7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).
8. Теорема 4.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт 5 замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .
Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядка: их виды, уравнения, примеры
Видео:Поверхности второго порядкаСкачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут



Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:




Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:




Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:




то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая


получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем 



получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:


Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:


Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

перепишем его в виде

Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

перепишем его в виде

Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :

I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:






Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :


Следовательно, общее уравнение определяет эллиптический параболоид.

I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:





Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением



I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.


Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Лекция 12. Уравнение поверхности и кривой в пространстве
Уравнением поверхности в пространстве Охуz называется уравнение F (х; у; z)= 0, которому удовлетворяют координаты каждой точки поверхности и только они.
Поверхность может, быть задана уравнением F (х; у; z)= 0(1), или, например, уравнением z = f (х; у)
Уравнение вида F (х; у)= 0 (2) определяет в пространстве цилиндрическую поверхность с образующими параллельными оси Оz и направляющей, лежащей в плоскости Оху и заданной в ней уравнением F (х; у)= 0. Уравнение поверхности составляется по схеме составления уравнения линии на плоскости.
Кривую в пространстве можно рассматривать как линию пересечения двух поверхностей; тогда она задается системой двух уравнений 
Если кривую рассматривать как траекторию движения точки, то она задается параметрическими уравнениями х = х(t), у = y(t), z = z(t), t Î[a; b]. (4)
Поверхности второго порядка
Если в пространстве R 3 ввести прямоугольную систему координат Охуz, то каждая поверхность определяется некоторым уравнением F (х, у, z) = 0, (х, у, z) –координаты любой точки поверхности. Если F (х, у, z) – многочлены не выше второй степени относительно совокупности переменных х, у, z, то уравнение F (х, у, z) = 0 называется уравнением второго порядка, а поверхность, изображаемая этим уравнением называется поверхностью второго порядка.
Если поверхность имеет специфическое расположение относительно системы координат (например, симметрична относительно некоторых координатных плоскостей, или имеет вершину в начале координат и пр.), то ее уравнение имеет достаточно простой вид, который называется каноническим.
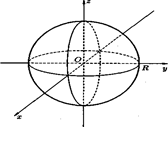
Сфера радиуса R с центром в начале координат x 2 + y 2 + z 2 = R 2 .
2) Эллипсоид с полуосями a, b, с и центром в начале координат
При а = b = с = R эллипсоид превращается в сферу радиуса R.
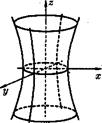
Сечения гиперболоида горизонтальными плоскостями z = h являются эллипсами
Сечения гиперболоида вертикальными плоскостями х = h являются гиперболами.

Сечения гиперболоида горизонтальными плоскостями z = h, |h| > c являются эллипсами
Сечения гиперболоида вертикальными плоскостями х = h или y = h являются гиперболами 
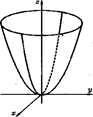

(2) Гиперболический
(3) Параболический у 2 = 2рх.
Метод параллельных сечений
Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей. Для решения этой задачи обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными плоскостям координат. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.
Пересечение поверхности с плоскостью
Линию в пространстве R 3 можно определить как пересечение двух поверхностей. Таким образом уравнение линии можно записать в виде системы 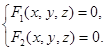
🌟 Видео
Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Кривые второго порядкаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Видеоурок "Гипербола"Скачать

Семинар Аналитическая геометрия. Кривые и поверхности второго порядка.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Поверхности 2го порядка. КлассификацияСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать