ЛЕКЦИЯ 4
Биореология
План лекции
Ньютоновские и неньютоновские жидкости. Уравнение Ньютона.
Динамическая и кажущаяся вязкость. Уравнение Шведова – Бингама.
Уравнение Бернулли.
Движение жидкости по трубам. Скорость течения.
Закон Пуазейля. Гидравлическое (периферическое) сопротивление.
Ламинарное и турбулентное течение. Число Рейнольдса.
Реологические свойства крови.
Ньютоновские и неньютоновские жидкости.
Уравнение Ньютона.
Реология – это раздел физики, изучающий силы сопротивления, возникающие в движущихся жидкостях и газах.
Жидкости не имеют своей формы. Они принимают всегда форму того сосуда, в котором они находятся. Основным параметром жидкости является её плотность r = m/V (кгм 3 ).
В жидкостях и в газах действует закон Паскаля: жидкости и газы передают давление во все стороны одинаково.То есть, если в какой-либо части объёма жидкости мы попытаемся повысить давление, то оно сразу распространится на весь объём жидкости. Величина давления измеряется в паскалях (Па) или Нм 2 . т.е. Р = F/S.
Представим себе, что внутри жидкости движется некоторая плоскость, причём, вектор её скорости направлен параллельно данной плоскости.
Слой жидкости, непосредственно прилегающий к этой плоскости, движется вместе с плоскостью с той же скоростью u. Отступив от плоскости на расстояние DY мы заметим, что скорость жидкости на этом расстоянии уменьшилась на величину Du . Таким образом, скорость слоёв жидкости уменьшается пропорционально увеличению расстояния от плоскости. Введём величину, которую назовём градиентом скорости:
grad u = Du/DY
Исаак Ньютон установил, что сила сопротивления, возникающая при движении тела в жидкости, пропорциональна градиенту скорости и величине плоскости:
F = -h(Du/DY)S
Это – уравнение Ньютона. Коэффициент h называется коэффициентом вязкости или динамической вязкостью. Он измеряется в Па . с .
Видео:Закон БернуллиСкачать

Коэффициент вязкости у каждой жидкости имеет своё собственное значение.
Он также зависит от температуры жидкости и не зависит от скорости сдвига.
Те жидкости, которые подчиняются уравнению Ньютона, называются идеальными или ньютоновскими. К ним относятся такие жидкости, как вода, одноатомные спирты, эфир, бензин, керосин, минеральное масло, и др.
Однако существуют жидкости, которые не подчиняются уравнению Ньютона и при подсчёте силы сопротивления по формуле Ньютона получается большая погрешность. Такие жидкости в своём составе имеют либо высокомолекулярные соединения, либо представляют собой эмульсии, суспензии различных форменных элементов. Например, яичный белок сырого яйца, кисель, молоко и его продукты, кровь и т.д.Их вязкость значительно больше.
Динамическая и кажущаяся вязкость.
Уравнение Шведова – Бингама.
Для того, чтобы понять следующий раздел, вспомним один из видов деформации твёрдого тела: деформацию сдвига. Представим себе куб, сделанный из какого-либо твёрдого тела. Приложим к его верхней грани сдвигающую силу F. Отношение этой силы к величине площади верхней грани S называется сдвиговым напряжением (Нм 2 ) .
F/S=t— напряжение сдвига
dv/dx=g — градиент сдвиговой скорости.
Шведов и Бингам установили связь между сдвиговой скоростью и напряжением сдвига. Они вывели уравнение, которое носит их имя:
t = to + Mg
to — предел текучести, т.е. минимальное напряжение, при котором жидкость начинает течь. По аналогии с твёрдым телом, to— это такое сдвиговое напряжение, при котором тело перестаёт восстанавливать свою форму после снятия деформирующей нагрузки.
M — структурная вязкость. Она более полно отображает вязкость жидкостей. Например, при движении крови по сосудам, вязкость зависит не только от форменных элементов, но и от эластичности стенок сосуда.
При увеличении скорости движения жидкости структурная вязкость стремится к определённому пределу, который называется кажущейся вязкостью:
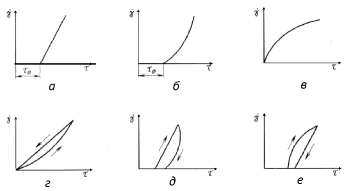
Графически изобразить уравнения Шведова – Бингама можно следующим графиком:
|
Следует отметить, что для ньютоновских жидкостей to равно нулю. Это значит, что в ньютоновских жидкостях сила трения покоя отсутствует полностью. Это можно обнаружить на таком примере. Предположим, что на поверхности абсолютно спокойной воды плавает какой-либо тяжёлый предмет (бревно). А вода является ньютоновской жидкостью, следовательно, плавающее тело можно привести в движение самой маленькой силой. Тоже бревно, лежащее на берегу, с места сдвинуть очень трудно, так как сила трения покоя при движении по поверхности твёрдого тела имеет значительную величину. Отсутствие в таких жидкостях силы трения покоя используется в точных навигационных приборах: компасах, гироскопах и пр. Следует добавить, что если ньютоновскую жидкость вылить на блюдце, то её поверхность сразу приобретает форму горизонтальной плоскости. С неньютоновской жидкостью наблюдается другая картина. Возьмём жидкость, являющуюся наиболее ярким представителем неньютоновских жидкостей: яичный белок. Если его вылить на блюдце, то его поверхность будет иметь форму небольшой горки, так как сила тяжести не в состоянии преодолеть до конца предел текучести жидкости.
Для очистки жидкостей от механических примесей используют фильтр из специальной пористой бумаги или ваты. Если нам приходится фильтровать воду, то мы заметим, что для фильтрации необходимо некоторое время. Если мы вместо воды возьмём спирт или бензин, то они через тот же фильтр будут профильтровываться быстрее, особенно бензин. Ведь чем меньше вязкость жидкости – тем быстрее она фильтруется. Надо сказать, что поддаются фильтрации все ньютоновские жидкости, даже такие, у которых высокая вязкость. Например, растительное масло будет тоже фильтроваться, но процесс фильтрации будет проходить медленно. А что будет, если мы попытаемся фильтровать неньютоновскую жидкость? Мы знаем, что наиболее ярким представителем ньютоновских жидкостей является яичный белок сырого яйца. Мы можем даже без практического опыта догадаться, что яичный белок вообще фильтроваться не будет, так как у него очень большой предел текучести. Не будут фильтроваться также и кисломолочные продукты. Строго говоря, все неньютоновские жидкости могут подвергаться процессу фильтрации, но для этого нужно их прогонять через фильтр действием дополнительной внешней силой. А силы тяжести для этого будет явно недостаточно.
Уравнение Бернулли
Рассмотрим движение идеальной жидкости по трубе произвольной формы и находящейся в произвольном положении.
Даниил Бернулли проанализировал движение жидкости по трубе и вывел уравнение, которое представляет собой закон превращения энергии для движущихся жидкостей. Для вывода данного уравнения, возьмём следующие узловые моменты. Во-первых учтём, что струя жидкости не разрывается, т.е. V1 = V2 (условие неразрывности струи. То есть: сколько жидкости втекает в трубу – столько и вытекает.
V1 = S1l1 V2 = S2l2
Согласно закону сохранения энергии, разность кинетических энергий струи на входе и на выходе равно работе внешних сил плюс разность потенциальных энергий на входе и на выходе.
Разность кинетических энергий:
Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

DEk = mv2 2 /2 – mv1 2 /2 = (rS2l2v2 2 — rS1l1v1 2 )/2
Работа внешних сил – это работа сил давления:
Ap = F1l1 – F2l2 = p1S1l1 – p2S2l2
Работа силы тяжести – это разность потенциальных энергий:
Ag = DEp = mgh1 – mgh2 = rS1l1gh1 — rS2l2gh2
Согласно закону сохранения энергии, сумма работ внешних сил и силы тяжести равна изменению кинетической энергии:
Ap + Ag = DEk
p1S1l1 – p2S2l2 + rS1l1gh1 — rS2l2gh2 = (rS2l2v2 2 — rS1l1v1 2 )/2
Данное выражение можно сократить, учитывая, что S1l1 = S2l2получим:
p1 –p2 + rgh1 -rgh2 = (rv2 2 — rv1 2 )/2
Произведём перегруппировку членов:
p1 + rgh1 + (rv1 2 )/2 = p2 + rgh2 + (rv2 2 )/2
p + rgh + (rv 2 )/2 = const
Это и есть уравнение Бернулли.
В этом уравнении первое слагаемое – внешнее давление; второе слагаемое – гидростатическое давление; третье слагаемое – гидродинамическое давление, т.е.давление жидкости, вследствие её движения. Как следует из уравнения Бернулли, как бы жидкость ни текла, что бы мы с ней ни делали, по какой трубе мы бы её ни направляли, всегда сумма этих трёх величин будет иметь постоянное значение. Если одна из этих величие уменьшится, значит возрастут другие, но сумма их всё равно останется постоянной.
Возьмём трубу переменного сечения и пустим по ней жидкость.
V1, p1 v2, p2 v3, p3
Согласно уравнению Бернулли, давление жидкости будет выше там, где скорость ниже и наоборот: где скорость выше, там будет давление ниже. На первый взгляд это противоречит здравому смыслу: как так: трубу сузили, а давление уменьшилось? И как насчёт закона Паскаля, не противоречит ли это ему? Но следует подчеркнуть, что закон Паскаля соблюдается только для неподвижных жидкостей, а в данном случае жидкость движется и поэтому, как следует из закона сохранения и превращения энергии, в суженной части, где скорость больше, давление должно быть меньше. Представим себе, что мы проделали сверху во всех участках этой трубы отверстия. Если бы жидкость была неподвижна, из всех отверстий били бы фонтанчики одной и той же высоты. Если бы жидкость была приведена в движение, то наблюдалась бы следующая картина: в широких частях трубы высота фонтанчиков бы увеличилась, а в узкой части – уменьшилась. При дальнейшем увеличении скорости жидкости высота фонтанчиков в узкой части трубы вообще уменьшилась бы до нуля, а при ещё большей скорости в этой части трубы давление стало бы ниже атмосферного и через это отверстие начал бы засасываться атмосферный воздух, т.е струя жидкости приобрела бы всасывающее действие.
Это явление используется на практике в пульверизаторе и в карбюраторе автомобильного двигателя. Это явление должны учитывать судоводители: когда суда идут параллельным курсом на небольшом расстоянии друг от друга, то возникает сила притяжения между ними. И если не принять соответствующие меры, суда могут стукнуться бортами и произойдёт авария. По этой же причине нельзя стоять рядом с быстро проходящим поездом: ведь проходящий поезд увлекает за собой огромную массу воздуха, а стоящий рядом человек создаёт между собой и поездом суженный канал, в котором, по закону Бернулли, создаётся пониженное давление и человек получает толчок в сторону поезда. А это может привести к несчастному случаю.
Поведение вязкопластического тела бингама описывается уравнением
ПРОДОЛЖЕНИЕ ЛЕКЦИИ № 6
Реологические модели и уравнения течения пищевых масс
Рассмотрим основные модели и виды течения пищевых масс. При этом необходимо указать, что точные математические закономерности получены только для ньютоновского течения. Для всех неньютоновских течений выведены лишь приближенные формулы.
Видео:Урок 137. Движение тела в жидкости и газе.Скачать

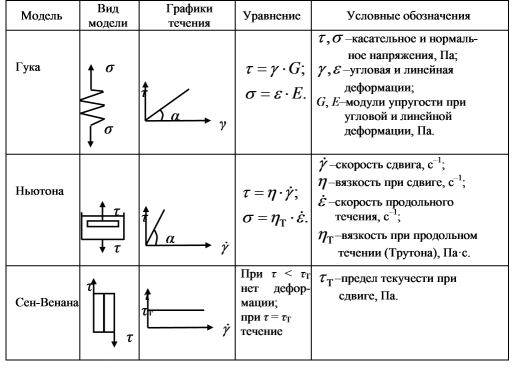
Известны три промежуточные модели идеализированных материалов (см. таблица 6.4): идеальноупругое тело (по Гуку), идеальнопластическое тело (по Сен-Венану), идеальновязкая жидкость (по Ньютону).
Идеальноупругое тело является системой, в которой энергия, затраченная на деформацию, накапливается в теле и может быть возвращена при разгрузке.
Идеальнопластическое тело может быть представлено в виде элемента, лежащего на плоскости с постоянным по величине трением, не зависящим от нормальной силы. Тело по Сен-Венану не начнет двигаться до тех пор, пока напряжение сдвига не превысит некоторого критического значения — предельного напряжения, после чего элемент может двигаться с любой скоростью.
Таблица 6.4. Реологические модели простых идеализированных тел
Идеальновязкая жидкость характеризуется тем, что в ней напряжения пропорциональны скорости деформации.
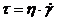
где h — коэффициент вязкости; 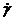
Вязкое течение, происходит под действием любых сил, как бы малы они ни были, однако скорость деформации при уменьшении сил снижается, а при их исчезновении обращается в нуль.
Модели могут быть скомбинированы параллельно или последовательно из двух или трех элементов: пружины (тело по Гуку), поршня (тело по Ньютону) и двух прижатых плоскостных элементов (тело по Сен-Венану). Они.
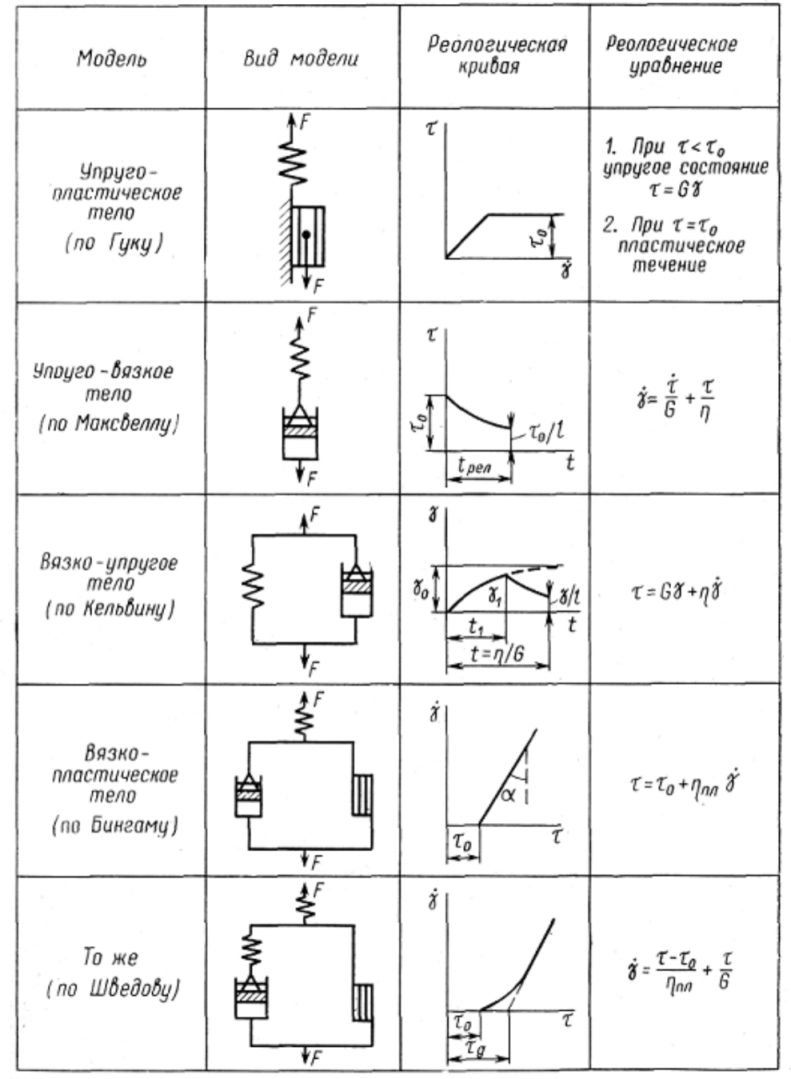
Наиболее сложные модели отражают следующие тела: упруго-пластическое, упруго-вязкое (по Максвеллу), вязко-упругое (по Кельвину), вязко-пластическое (по Шведову-Бингаму) (рис. 6.1).
Рис. 6.1. Реологические модели:
t — напряжение сдвига, Па; t0 — предельное напряжение сдвига, Па; G — модуль сдвига, Па; g — угловая деформация; — скорость сдвига, с; h — вязкость, Па·с; hпл — пластическая вязкость, Па·с.
Модель упруго-пластического тела получается при последовательном соединении упругого и пластического элементов.
Модель упруго-вязкого релаксирующего тела по Максвеллу — это последовательно соединенные гуковский и ньютоновский элементы. Тело по Максвеллу ведет себя как упругое или как вязкое в зависимости от отношения времени релаксации к длительности эксперимента. Итак, если под действием мгновенного усилия пружина растягивается, а затем нагрузка сразу снимается, то поршень не успевает двигаться и система ведет себя как упругое тело. Однако, с другой стороны, если поддерживать растяжение пружины постоянным, она постепенно релаксирует, перемещая поршень вверх, и система ведет себя почти как ньютоновская жидкость.
Модель вязко-упругого тела по Кельвину — параллельное соединение упругого и вязкого элементов. Под действием растягивающего усилия пружина удлиняется, а поршень будет двигаться в жидкости. Движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пружины наступает не сразу. Когда нагрузка устранена, пружина сжимается до первоначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.
Модель тела по Кельвину отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после ее снятия.
Модель вязко-пластического тела по Шведову—Бингаму характеризует материалы, которые в первом приближении можно рассматривать как тела по Сен-Венану. Они начинают течь, когда напряжение сдвига достигает предельного напряжения. Если нет вязкого сопротивления, то скорость течения материала станет сколь угодно большой. Во втором приближений такие материалы должны обладать еще вязкостью. Все это приводит к постулированию идеального тела, реологическое уравнение которого предложено Бингамом.
Модель тела по Шведову отличается от модели по Бингаму тем, что параллельно телу по Сен-Венану присоединено тело по Максвеллу, а параллельно телу по Бингаму — тело по Ньютону.
В технологии пищевых производств встречается много материалов, которые не подчиняются закону Ньютона; вязкость их при заданных температуре и давлении не остается неизменной, а зависит от скорости деформации и других факторов, поэтому зависимость напряжения от скорости сдвига имеет нелинейный характер. Эти материалы получили название неныотоновских веществ (аномальных). Одно и то же вещество в зависимости от концентрации может проявлять различные виды течения.
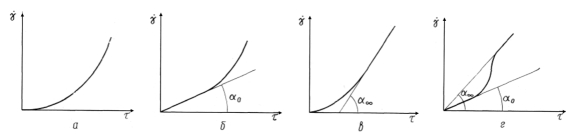
Рассмотрим наиболее типичные виды кривых течения псевдопластического материала (рис. 6.2).
Рис. 6.2. Кривые течения псевдопластических материалов.
Уравнение Оствальда (степенной закон) описывает кривую, представленную на рис. 6.2, а,
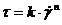
Уравнение (6.2) является эмпирическим, имеющим два параметра: константу k, зависящую от природы материала и геометрических размеров измерительной аппаратуры, и константу n, являющуюся индексом течения.
При 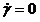
Степенной закон получил широкое распространение для описания вязкости различных неньютоновских пищевых материалов: томатных паст, сахарных сиропов, абрикосового пюре, хлебопекарного теста, конфетных масс, крахмальных суспензий, майонеза, мыла и некоторых других.
На рис. 6.2, б приведена кривая (реограмма), которая может быть описана уравнением Штейгера,
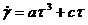
Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

где а, с — эмпирические коэффициенты.
Уравнение (6.3) действительно также и при 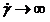
На рис. 6.2, в и г приведены кривые течения псевдопластиков, отличающихся аномалией при малых (в) или высоких (г) скоростях сдвига.
Дисперсные системы при напряжениях, меньших предельного, ведут себя как твердые тела и упруго деформируются, при напряжении, превышающем предельное, становятся пластичными. Различают несколько видов пластического течения (рис. 6.3).
Идеальнопластическое — течение, начинающееся после достижения предельного напряжения, когда наблюдается пропорциональность между скоростью и напряжением сдвига. Для характеристик этого вида течения Бингам предложил уравнение (рис. 6.3, а)
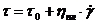
где t0 — предельное напряжение сдвига, Па; hпл — пластическая вязкость, Па·с.
Примером систем, довольно близко следующих уравнению Бингама, могут служить маргарин, шоколадные смеси, зубная паста, жидкие мыла и моющие средства, сырково-творожные и конфетные массы.
Рис. 6.3. Кривые течения пластических материалов:
а — тело по Бингаму; б — тело по Балкли-Гершелю; в — дилатантные материалы; г — тиксотропные материалы; д — антитиксотропные материалы; е — реопексные материалы.
Кривые течения некоторых пищевых материалов описываются уравнением Балкли-Гершеля (рис. 6.3, б) (например, масса для конфет «Русский узор»),
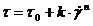
Пластическое течение, при котором не наблюдается пропорциональной зависимости между скоростью сдвига и напряжением, называется неидеально-пластическим.
При достижении предела текучести структура разрушается не сразу, а постепенно, по мере увеличения градиента скорости.
Кассон предложил для подобного рода течения следующее уравнение:
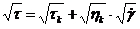
где tК — предельное напряжение по Кассону, Па; hК — пластическая вязкость по Кассону, Па·с.
Уравнение (6.6) было применено при описании течения расплавленного шоколада, сливочного масла, вафельного теста и сгущенного молока.
Дилатантное течение характерно для веществ, у которых с увеличением скорости сдвига возрастает вязкость (рис. 6.3, в). Это течение описывается уравнением (6.5) при n >1. При очень высоких напряжениях вязкость может стать бесконечно большой, что приведет к разрушению вещества. Примером дилатантных материалов могут служить сгущенное молоко, полимерный клей для сигарет, некоторые растворы сахара, крахмала и т. п.
На рис. 6.3, г, д и е приведены кривые течения соответственно тиксотропных, антитиксотропных и реопексных материалов.
Материал считается тиксотропным, когда вязкость его является функцией времени, причем предполагается, что структура после определенного времени покоя возвращается к первоначальному состоянию. Время тиксотропного разрушения, так же как и восстановления, для различных структур изменяется в очень широких пределах. Тиксотропия может быть определена по реограмме при получении кривой гистерезиса.
Материалы, состояние течения которых во времени является противоположным тому, какое дают тиксотропные системы, называют антитиксотропными.
Вещества, структура которых во времени упрочняется, обладают свойствами реопексии.
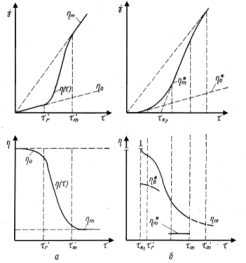
Высокомолекулярные системы разделяют на две группы: жидкообразные и твердообразные с постепенным переходом между ними (рис. 6.4).
Если истинновязкие жидкости характеризуются постоянным значением вязкости, то структурированные жидкости определяются зависимостью эффективной вязкости от действующего напряжения и двумя областями напряжений с постоянным значением вязкости: наибольшей предельной вязкостью h0 практически неразрушенной структуры и наименьшей вязкостью hт предельно разрушенной структуры, где hт остается постоянной. Твердообразность тела выражается тем резче, чем значительнее разность между h0 и hт. Переходными между h0 и hт являются значения эффективной переменной вязкости, убывающей с ростом напряжения (или градиента скорости).
Рис. 6.4. Зависимость скорости сдвига и вязкости от напряжения для жидкообразных (а) и твердообразных (б) систем.
Для практических расчетов при больших градиентах скорости могут быть введены величины: условный динамический предел текучести 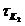
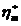
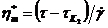
окажется значительно меньше h0, то кривая течения аппроксимируется прямой Бингама.
Для области несколько выше условного статического предела текучести 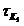
Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Истиннопластические тела характеризуются наличием истинного предела текучести, совпадающего с пределом упругости, т.е. таким предельным напряжением сдвига, ниже которого экспериментально никакого течения не обнаруживается.
Для научного обоснования задач технологической обработки пищевых материалов большое значение имеет изучение процессов структурообразования систем. П. А. Ребиндер предложил разделить структуры на коагуляционные (тиксотропно-обратимые) и конденсационно-кристаллизационные (необратимо разрушающиеся) .
Коагуляционные структуры возникают под действием связей и других нековалентных молекулярных сил сцепления коллоидных частиц, участвующих в интенсивном броуновском движении, и более крупных частиц, находящихся в суспензии. Кинетика тиксотропного восстановления структуры вызывается интенсивным броуновским движением, в результате которого частицы сцепляются друг с другом и более крупными конгломератами по коагуляционным участкам или по местам наибольшего сближения поверхностей.
Конденсационно-кристаллизационные структуры образуются в результате срастания мелких кристаллов, образующихся в растворах, в пространственные системы или развития химических ковалентных связей. Такие структуры весьма прочны и механически разрушаются необратимо.
Рис. 6.5. Кривые кинетики деформации.
Для определения упруго-пластично-вязких свойств дисперсных систем и растворов высокополимеров предложено экспериментальное определение семейства кривых деформации чистого сдвига e — время t, полученных при σ=const (рис. 6.5). При испытаниях проводятся в области упругих обратимых деформаций (рис. 6.5, а), при 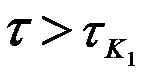
Наиболее важным реологическим показателем свойств материала является зависимость скорости деформации от напряжения. Для большинства пищевых масс эта зависимость имеет сложный характер. В этих случаях реологические свойства характеризуются кривой зависимости скорости деформации от напряжения, называемой кривой течения, или реограммой.
Объемная деформация пищевых масс
В тестоделителях для хлебопекарного теста, делительно-закаточных машинах для бараночных заготовок, макаронных прессах, прессах для отжима масла и соков, машинах для формования конфетных масс, грануляторах, машинах для таблетирования и т. п. обрабатываемые пищевые массы находятся в условиях всестороннего сжатия. При этом происходит их уплотнение сначала в результате удаления воздуха или жидкости, а затем переориентации и более плотной упаковки частиц массы в основном благодаря пластической деформации.
При машинной обработке и формовании пищевых масс всегда одновременно происходят деформации сдвига и сжатия. Изучение «поведения» масс при объемной деформации дает возможность увязать конструкцию и прочность рабочих органов и кинематику машин с физико-механическими свойствами перерабатываемых масс.
При изучении объемной деформации материала под давлением в условиях всестороннего сжатия обычно решаются следующие задачи: распределение давления в объеме массы, сжимаемость материала под давлением, зависимость плотности массы от давления, процессы релаксации напряжений и ползучести.
Исследование «поведения» макаронного теста в условиях всестороннего сжатия показало, что давление в тесте распространяется неодинаково: давление в осевом направлении превышает радиальное на 10-15%. В интервале изменения влажности от 28 до 33% стабилизация процесса всестороннего сжатия наступает при давлении 3 МПа. При испытании хлебопекарного теста было установлено, что давление в тестовой массе при сжатии распределяется также неравномерно и зависит от длительности приложения силы на нагнетателе. Превышение давления прессования над заданным рабочим определяется размерами тестовой камеры технологической машины и физико-механическими свойствами теста.
При многократном нагружении хлебопекарного теста наибольшее увеличение плотности происходит после первого нагружения, при дальнейших нагружениях изменение плотности незначительно. Основные изменения плотности наблюдались при давлениях до 0,15-0,2 МПа. После пятикратного нагружения давлением 0,25 МПа плотность теста из муки I сорта влажностью 46,4% увеличилась на 27,5%, теста влажностью 42,2% — на 21%, теста для украинского хлеба — на 18%. После разгрузки системы (при сохранении получен-ной деформации) давление во времени медленно уменьшается.
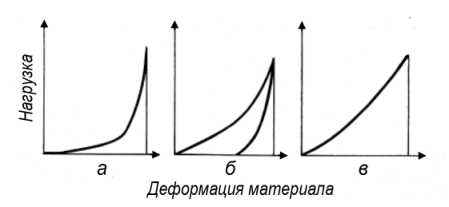
Характерные кривые прессования для различных пищевых материалов (макаронного и бараночного теста, пралиновых конфетных масс, чая, кофе и т.п.) приведены на рис. 6.6. По кривым видно, что до образования сплошной однородной структуры с максимальным уплотнением массы вначале происходит резкое изменение плотности от давления, а затем наблюдается незначительное повышение плотности при резком увеличении давления.
Практически различают трудно- и легкоуплотняемые материалы. Трудно-уплотняемыми являются такие, которые после длительной зоны предвари-тельного уплотнения (без большой затраты энергии) незадолго до максимального уплотнения могут воспринимать большие нагрузки без заметного уплотнения (рис. 6.6, а). Другие трудноуплотняемые материалы обладают большим упругим последействием (рис. 6.6, б). Диаграмма прессования легкоуплотняемых материалов (рис. 6.6, в) имеет короткую зону предуплотнения, нагрузка медленно возрастает на протяжении всего времени прессования.
От физико-механических свойств перерабатываемого материала, его дисперсности и температуры, объема конечного спрессованного продукта зависят: величина зоны предварительного уплотнения, упругость массы, работа, затрачиваемая на изменение формы, и скорость нагружения материала.
Рис. 6.6. Кривые прессования.
При определении зависимости плотности бараночного теста от давления было выяснено, что вначале происходит сжатие теста, имеющего большое количество газовых включений. При этом зависимость имеет криволинейный характер. После уплотнения теста при давлении выше 0,8 МПа эта зависимость принимает линейный характер. Так как в рабочих цилиндрах делительно-закаточных бараночных машин при формовании тестовых заготовок давление превышает 0,8 МПа, то для практических расчетов представляет интерес линейная зависимость.
Количество получаемой жидкой фазы при прессовании масличных материалов, плодов, ягод зависит от величины рабочего давления, характера связи жидкости с материалом, содержания жидкой фазы в исходном материале и остатке, температуры процесса, толщины прессуемого слоя и продолжительности процесса. Жидкая фаза в прессуемых продуктах находится в свободном и связанном состоянии. Свободная жидкость легко отделяется от сухого вещества материала. Для отделения осмотической и адсорбционно связанной влаги требуется затрата значительной энергии, что происходит, например, при сушке.
Перед отжатием пищевые материалы подвергаются механической, термической, электрофизической обработке. Механическая обработка заключается в измельчении материала с целью разрушения клеточных оболочек, препятствующих выходу жидкости из клеток. При тепловой и электрофизической обработке происходят более сложные процессы, но цель та же: подготовить сырье к наиболее полной отдаче жидкой фазы при прессовании.
Физическая сущность отжатая жидкой фазы при прессовании заключается в следующем. В начальный период прессования материала его частицы сближаются и жидкость, находящаяся на поверхности частиц, движется по каналам между частицами, а затем жидкость перемещается в слое пористого материала по капиллярам переменного сечения и направления, т. е. осуществляется фильтрация жидкой фазы в слое.
Как было указано выше, отжатие массы материала при прессовании связано с фильтрацией, при которой отжимаемая жидкость должна проходить по сложной системе капилляров с переменным сечением. Следовательно, при прессовании происходит фильтрация, которую в общем виде можно описать законом Пуазейля
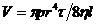
где V — объем жидкости, проходящей через канал за время t, м 3 ; р — потеря напора в капилляре, Па; r — радиус капилляра, м; 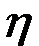
Прессование — более сложный процесс, чем процесс фильтрации жидкости по капиллярам. Однако анализ уравнения Пуазейля позволяет сделать некоторые практические выводы. Из этого уравнения следует, что при прессовании нерационально увеличивать толщину слоя и целесообразно повысить температуру массы. Более полному отжатию жидкости способствуют увеличение давления и уменьшение вязкости жидкости. Но, с другой стороны, увеличение давления уменьшает сечение капилляров, а следовательно, и производительность прессов. Поэтому оптимальное рабочее давление при прессовании устанавливается опытным путем с учетом свойств материала, количества и качества получаемой жидкой фазы.
Изменение объема теста зависит от сжимаемости газовых пузырьков и деформации структурной сетки, более компактной «упаковки» твердой дисперсной фазы в дисперсионной среде.
Видео:Физика. 10 класс. Неньютоновские жидкостиСкачать

Существенное влияние на условия объемной деформации и течения пищевых масс при их прессовании, формовании и транспортировании по трубам оказывают релаксация давления и ползучесть материала. В пищевой промышленности эти явления изучены для хлебного, макаронного и бараночного теста, различных конфетных масс, байхового чая и некоторых других продуктов.
Особый интерес релаксация представляет для циклических процессов формования (отсадка конфет, печенья, кремов), так как период релаксации несколько больше разности между временем кинематического цикла и временем выдавливания массы в реальных отсадочных машинах. Это приводит к тому, что внутренние напряжения не успевают рассасываться в период между отсадками и масса, сохраняя упругое последействие, после остановки нагнетательных органов продолжает выпрессовываться через отверстия матрицы, что препят-ствует образованию корпусов изделий заданной формы. При перекрывании отверстия в момент остановки нагнетателя остаточные напряжения в массе способствуют ее уплотнению и синерезису. Следовательно, при отсадке (особенно сбивных масс) необходимо принудительное снятие напряжений в массе в период между двумя отсадками.
Испытания различных вязко-пластических и псевдопластических пищевых масс (конфетных, макаронного (хлебного и бараночного теста и т. п.) показали, что с повышением давления все реологические характеристики возрастают. Например, при увеличении давления от 0 до 49 кПа на пралиновые конфетные массы вязкость увеличивается в 1,5-2,5 раза, а предельное напряжение сдвига — в 2-3 раза. При повышении давления происходит уплотнение массы, причем график прессования пищевых материалов имеет нелинейный вид, что обусловливает и непостоянство влияния на структурно-механические свойства.
Опыты с бараночным тестом позволили установить, что с повышением избыточного давления от 0 до 2,45 МПа вязкость увеличивается в 1,2-1,4 раза, а предельное напряжение сдвига — примерно в 3 раза. Для макаронного теста при изменении давления от 3,5 до 9 МПа наблюдается увеличение вязкости примерно в 1,5-1,8 раза и предельного напряжения сдвига в 1,4-1,5 раза. Подводя итог влиянию давления на реологические свойства пищевых материалов, следует отметить, что давление влияет на качество готовой продукции. Поэтому при расчете того или иного процесса нужно стремиться к тому, чтобы обработка пищевых материалов производилась при оптимальном давлении.
📽️ Видео
Лекция II-4. Математические модели твердого телаСкачать

мацирация кожиСкачать
45_09_фев_16 ВязкостьСкачать

Лекция II-4. Математические модели твердого телаСкачать

Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Галилео. Эксперимент. Неньютоновская жидкостьСкачать

Реология материалов. ВведениеСкачать

20. С.В. Головин. Моделирование гидроразрыва пласта: теория и экспериментСкачать

Галилео. Эксперимент. Вязкость воздухаСкачать

НЕНЬЮТОНОВСКАЯ ЖИДКОСТЬСкачать

Жидкости. Часть 7 (видео 8) | Жидкости | ФизикаСкачать

Изучаем вязкость жидкости. Обучающее видеоСкачать

Гипоталамус и поведениеСкачать