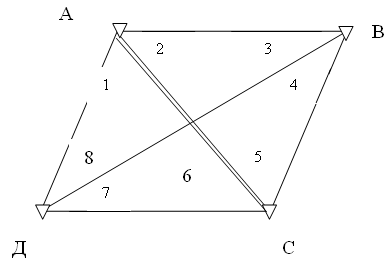
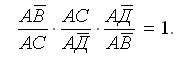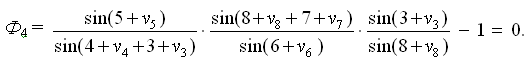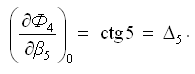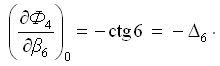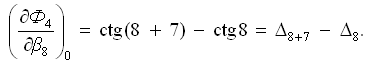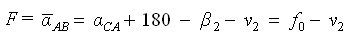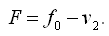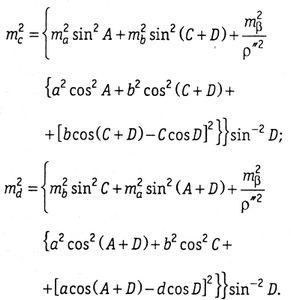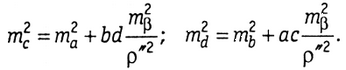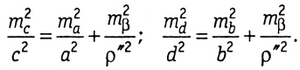Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n — t = 8 — 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
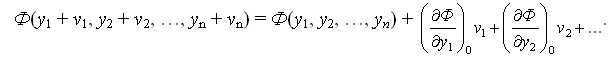
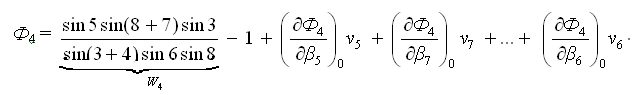
Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
| . | Числитель | . | . | Знаменатель | . |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
Полюсное условное уравнение поправок принимает вид:
Составим весовую функцию.
— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
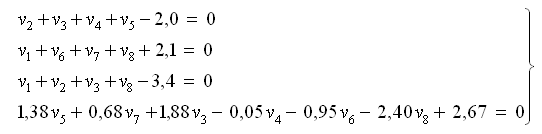
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| . | ||||||
| -1 | . | |||||
| +1.88 | . | |||||
| -0.05 | . | |||||
| +1.38 | . | |||||
| -0.95 | . | |||||
| +0.68 | . | |||||
| -2.40 | . |
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения — m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции — mF.
Вычислите уравненные значения углов 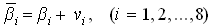
Дата добавления: 2016-06-24 ; просмотров: 3761 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Все о геодезический четырехугольник
- Использование способа бездиагональных четырехугольников
- Уравнивание геодезического четырехугольника коррелатным способом
- Уравнивание геодезического четырехугольника
- Уравнивание геодезического четырехугольника.docx
- «ВЫСШАЯ ГЕОДЕЗИЯ Допущено Государственным комитетом СССР по народному образованию в качестве учебника для студентов геодезических специальностей вузов М О С К В А Н Е Д Р А 1989 Б Б К . »
- § 129. ЧИСЛО НЕЗАВИСИМЫХ УСЛОВНЫХ УРАВНЕНИИ
- В ТРИАНГУЛЯЦИИ
- СВОБОДНЫХ ЧЛЕНОВ УСЛОВНЫХ УРАВНЕНИИ
- § 132. ПОСЛЕДОВАТЕЛЬНОСТЬ УРАВНИТЕЛЬНЫХ ВЫЧИСЛЕНИИ.
- ОЦЕНКА ТОЧНОСТИ
- УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ
- ПАРАМЕТРИЧЕСКИМ СПОСОБОМ
- § 133. ПОСЛЕДОВАТЕЛЬНОСТЬ УРАВНИТЕЛЬНЫХ ВЫЧИСЛЕНИИ.
- СООТНОШЕНИЕ ВЕСОВ ИЗМЕРЕННЫХ ВЕЛИЧИН
- НОРМАЛЬНЫХ УРАВНЕНИИ
- НА ПУНКТАХ ТРИАНГУЛЯЦИИ И ПОЛИГОНОМЕТРИИ
- ОЦЕНКА ТОЧНОСТИ
- ВЫСШАЯ ГЕОДЕЗИЯ
- ВНИМАНИЮ НАУЧНЫХ
- И ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ
- РАБОТНИКОВ, АСПИРАНТОВ
- СПРАВОЧНЫЕ П О С О Б И Я,
- СВОЕВРЕМЕННО ОФОРМЛЕННЫЙ ЗАКАЗ
- ГАРАНТИРУЕТ ПРИОБРЕТЕНИЕ
- НУЖНОЙ ВАМ КНИГИ.
- АДРЕСА ОПОРНЫХ МАГАЗИНОВ
- ИЗДАТЕЛЬСТВА «НЕДРА»
Видео:Коррелатный способ. Решение системы условных уравненийСкачать

Все о геодезический четырехугольник
Использование способа бездиагональных четырехугольников
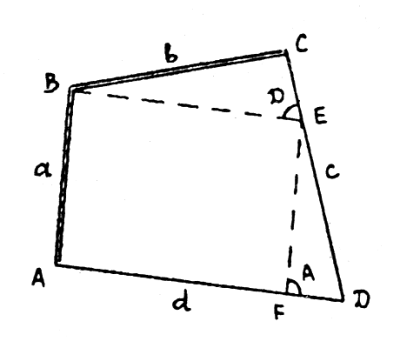
Этот способ удобен при развитии геодезической сети по проездам и просекам, а также при создании строительной сетки. В четырехугольнике без диагоналей необходимо измерить две стороны и все углы четырехугольника. На рисунке 1.10 в четырехугольнике измерены стороны а и b , нужно определить стороны c и d . Через точку В проведем линию , BE , параллельную AD , а через точку Е — линию ЕЕ , параллельную АВ .
Рис. 1.10 . Четырехугольник без диагоналей
Используя теорему синусов, имеем
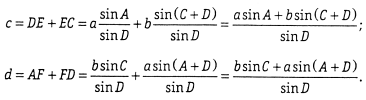
В сложных сетях необязательно измерять стороны в каждом четыреху-гольнике, их можно определить из вычислений по полученным формулам. При равноточных угловых измерениях средние квадратические ошибки сторон определяют по формулам, полученным с учетом формул (1.6), и формуле средней квадратической ошибки функции:
Для прямоугольного четырехугольника с предварительно уравненными углами
В цепи прямоугольных четырехугольников, уравненных за условия фигур, в которой измерены стороны а и b
Видео:Четырехугольники. Вебинар | МатематикаСкачать

Уравнивание геодезического четырехугольника коррелатным способом
Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n — t = 8 — 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
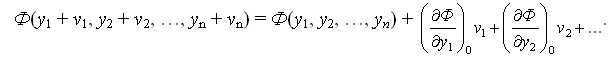
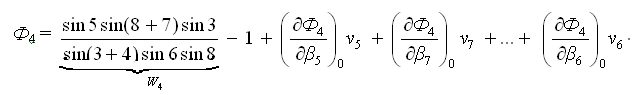
Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
| . | Числитель | . | . | Знаменатель | . |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
Полюсное условное уравнение поправок принимает вид:
Составим весовую функцию.
— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
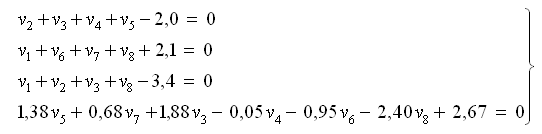
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| . | ||||||
| -1 | . | |||||
| +1.88 | . | |||||
| -0.05 | . | |||||
| +1.38 | . | |||||
| -0.95 | . | |||||
| +0.68 | . | |||||
| -2.40 | . |
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения — m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции — mF.
Вычислите уравненные значения углов 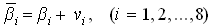
Дата добавления: 2016-06-24 ; просмотров: 3716 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Условная вероятностьСкачать

Уравнивание геодезического четырехугольника
Автор работы: Пользователь скрыл имя, 02 Апреля 2013 в 10:23, реферат
Краткое описание
Исходные данные: ХВ и YВ; ХD и YD.
В геодезическом четырехугольнике измерены восемь углов на четырех точках (рисунок 32). Углы нумеруются цифрами 1-8 по ходу часовой стрелки. Необходимо определить координаты пунктов А и С, а также дирекционные углы и длины сторон.
Вложенные файлы: 1 файл
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Уравнивание геодезического четырехугольника.docx
Уравнивание геодезического четырехугольника
В геодезическом четырехугольнике измерены восемь углов на четырех точках (рисунок 32). Углы нумеруются цифрами 1-8 по ходу часовой стрелки. Необходимо определить координаты пунктов А и С, а также дирекционные углы и длины сторон.
1. В геодезическом четырехугольнике возникают следующие условия:
— сумма всех восьми углов в четырехугольнике должна быть равна 360°;
— геодезический четырехугольник рассматривается как центральная система с фиктивным полюсом – точкой О пересечения диагоналей;
— в фиктивных треугольниках АВО, DОС, ВСО и АОD должны существовать следующие условия суммы углов: 1+2 = 5+6; 3+4 = 7+8;
— все измеренные углы можно рассматривать как связующие углы треугольников центральной системы, следовательно, возникает полюсное условие.
условий фигур – 3;
условие полюса – 1.
2. Невязки за условия фигур вычисляются по формулам:
w1 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 — 360°;
w2 = 1 + 2 – 5 – 6; (209)
Допустимая невязка wдоп = 2,5 mb Ön; (210)
Первичные поправки V¢ вычисляем по формулам:
Вычисление поправок контролируется: их сумма в четырехугольнике должна равняться невязке с обратным знаком.
3. За полюс принята точка пересечения диагоналей. Тогда условное уравнение полюса, как и в центральной системе, можно выразить формулой:
wП = [ ( lg sin1 + lg sin3+ lg sin5 + lg sin7) –
– ( lg sin2 + lg sin4+ lg sin6 + lg sin8) ] 10 6 (212)
где b — это изменение логарифма синуса угла при изменении самого угла на одну секунду в шестом знаке логарифма.
Для вычисления вторичных поправок за условие полюса определяем коррелату К
Введением вторичных поправок заканчивается процесс уравнивания горизонтальных углов. После чего решением треугольников находят стороны, вычисляют дирекционные углы и приращения координат. Полученные невязки приращений распределяют пропорционально длинам сторон и вычисляют окончательные координаты пунктов.
Видео:Полярная система координатСкачать

«ВЫСШАЯ ГЕОДЕЗИЯ Допущено Государственным комитетом СССР по народному образованию в качестве учебника для студентов геодезических специальностей вузов М О С К В А Н Е Д Р А 1989 Б Б К . »
Выражение (18.16) представляет собой в общем виде ус ловное уравнение, приведенное к линейному виду, как это при нято при уравнивании геодезических сетей.
Д л я приведения к линейному виду полюсного условного уравнения (18.11) геодезического четырехугольника (см.
рис. 113, а) обозначим р sin V I sin (1 + V I I I ) sin I V =
проекций Следует отметить, что при уравнивании сети по направле ниям сумма коэффициентов при поправках в любом условном уравнении должна быть равна нулю, так как после замены по правок в углы поправками в направления коэффициенты при них будут иметь один раз положительный, а второй раз отри цательный знаки. Это требование используется в качестве про межуточного контроля вычислений при уравнивании направле ний.
Условия проекций. Они возникают в том случае, когда в сети имеется длинная диагональ, соединяющая вершины не смежных треугольников и при ней измерены один или два из быточных угла (рис. 115).
Введем вспомогательную систему координат с началом в точке А ось абсцисс направим вдоль диагонали AD, а ось ор динат по перпендикуляру к ней. Суть условия проекций сво дится к тому, что в замкнутом контуре ABCDA сумма проекций длин его сторон на любое направление должна быть равна нулю. Так как длина диагонали AD не известна, то направле ние у на которое проектируют длины сторон, совмещают с пер у
В выражении (18.25) (At/) —поправки в приращения Ау вычисленные в условной системе координат ху с началом в точке Л. Поправки (Ау) следует выразить через поправки в измеренные направления (углы) и затем получить условное уравнение в окончательном виде.
Условия проекций не ведут к повышению точности сети; они только усложняют процесс уравнительных вычислений, поРис. 116. Цепочка треугольников Рис. 117. Вставка пункта в жесткий между пунктами с заданными коор- угол, заданный координатами трех динатами исходных пунктов скольку имеют достаточно громоздкий вид. Поэтому проекти ровать геодезические сети следует таким образом, чтобы усло вия проекций не возникали.
В фигуре ABCDA (см. рис. 115) измерено два дополнитель ных угла р. Поэтому в ней возникнет два дополнительных ус ловия: условие проекций и условие фигуры. В аналогичной фи гуре (см. рис. 115, б ), где измерен один дополнительный угол Р, возникнет дополнительно только условие проекций.
Базисные условия возникают при наличии в сети избыточ ных исходных сторон (непосредственно измеренных или вычис ленных по координатам исходных пунктов). При составлении базисного условия выделяют в сети цепочку треугольников, со единяющую ближайшие исходные стороны Ь и Ь по наикрат 2 чайшему пути.
Длина исходной стороны Ь, вычисленная по уравненным
быть равна заданному значению ее. Например, в цепи тре угольников (рис. 116) между двумя исходными (жесткими) сторонами Ь и Ь вычисленными по координатам исходных 2у
Пусть Л = Л ‘ + ( Л ) и В = В’+(В), где (А) и ( 5 ) — п о п р а в к и из уравнивания в измеренные углы А’ и В’. Приведя уравнение (18.27) к линейному виду, получим
(18.34) где свободный член со вычисляется по формуле (18.29).
При уравнивании триангуляции по направлениям поправки в углы выражают через поправки в направления.
Условия дирекционных углов возникают при наличии в сети избыточного числа исходных дирекционных углов (непосред ственно измеренных или вычисленных по координатам исход ных пунктов). При составлении условия дирекционных углов выделяют в сети цепочку треугольников, соединяющих исход ные дирекционные углы ai и а по наикратчайшему пути (см. 2 рис. 116, 118).
Дирекционный угол а вычисленный по уравненным углам 2у треугольников относительно дирекционного угла оы, должен быть равен заданному значению его. В том случае, когда ди рекционные углы ai и а заданы координатами исходных пунк
где свободный член со вычисляется по формуле (18.37).
При уравнивании триангуляции по направлениям поправки в углы следует выразить через поправки в направления.
Условные уравнения абсцисс и ординат. Условные уравне ния координат (абсцисс и ординат) возникают только в том случае, если в сети триангуляции имеются раздельные группы исходных (жестких) пунктов, удаленные одна от другой не ме нее чем на две определяемые стороны. Отдельная группа ис ходных пунктов может состоять либо из одного такого пункта, либо из нескольких смежных пунктов. Например в одну группу исходных пунктов входят два смежных пункта Л и В, а в дру гую, удаленную от первой на две определяемые стороны ВС и CD — один исходный пункт D (рис. 119).
При составлении условий координат в сети выделяют це почку треугольников, соединяющую ближайшие пункты разных групп исходных пунктов, и в ней намечают ходовую линию,
где Ах’ и Ау’ — приращения координат, вычисленные с исполь зованием измеренных углов А’, В’, С в треугольниках; (Ах), (Ау) — поправки в их значения из уравнивания сети.
Д л я получения условий координат в окончательном виде по правки (Ах) и (Ау) в приращения координат следует выразить через поправки (Л), ( В ), (С) в измеренные углы в треугольни ках. Выполнив эти преобразования, получим для случая урав нивания триангуляции по углам:
условное уравнение абсцисс
нат (в км) последнего пункта D ходовой линии и координат текущих пунктов ходовой линии, включая исходный пункт В в начале этой линии; (А) и (В) — поправки в связующие углы Л и В в треугольниках, при этом измеренный угол В лежит против исходной, а угол Л — против определяемой в треуголь нике стороны; (С)—поправки в промежуточные углы С, при этом поправка (С) имеет знак плюс ( + С), если угол С распо ложен слева от ходовой линии, и знаком минус (—С), если справа от нее, идя от начального пункта В этой линии к конеч ному пункту D.
Свободные члены о) и щ (в м) находят по формулам ж
D ходовой линии.
При уравнивании триангуляции по направлениям поправки в углы выражают через поправки в измеренные направления.
Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

§ 129. ЧИСЛО НЕЗАВИСИМЫХ УСЛОВНЫХ УРАВНЕНИИ
Видео:УДИВИТЕЛЬНЫЙ способ решения уравнения ★ Вы такого не видели! ★ Уравнение четвертой степениСкачать

В ТРИАНГУЛЯЦИИ
При уравнивании триангуляции по углам для определения k вновь определяемых пунктов необходимо измерить 2k необхо димых углов. При уравнивании триангуляции по направлениям следует измерить (2k+t) необходимых направлений, где t — число пунктов, на которых выполнены угловые измерения. При этом tn, где п — число всех пунктов в сети (исходных и опре деляемых).
Общее число S независимых условных уравнений в геодези ческой сети равно числу избыточных измерений в ней, т. е.
равно разности числа всех измерений в сети и минимального числа измерений, необходимых для вычисления координат всех определяемых пунктов. Число S независимых условных уравне ний находится по формулам:
при уравнивании триангуляции по направлениям S„ = D + k + k — (2k +1), (18.46) s a
ренных непосредственно (не вычисленных по координатам) ба зисных сторон и азимутов сторон соответственно; k — число определяемых пунктов; t — число пунктов, на которых выпол нены угловые измерения; Л^ —число измеренных углов в сети.
В том случае, когда в сети непосредственно не измерялись ни базисные стороны, ни азимуты сторон (см. рис. 116) прини мают k = k = 0.
s a Число независимых условных уравнений по видам опреде ляют следующим образом.
Число условий горизонта при уравнивании триангуляции по углам равно числу q полюсов центральных систем, на кото рых выполнены угловые измерения, т. е.
q = N + t—D. (18.48) При уравнивании триангуляции по направлениям условия горизонта не возникают.
Число f независимых условий фигур при уравнивании сети по направлениям найдем по формуле f = D-t-p+, (18.49) а при уравнивании сети по углам f^N-p-q+h (18.50) где р — число всех сторон в сети (исходных и определяемых).
Число условий фигур не зависит от того, как уравнивается сеть — по углам или по направлениям. Поэтому формулы (18.49) и (18.50) дают тождественные результаты, что может служить контролем вычислений.
Число с полюсных условных уравнений равно числу избы точных сторон в сети. Определяется оно по формуле с = р—2л+ 3, (18.51) где р — число всех сторон в сети; п — число всех пунктов в ней (исходных и определяемых). В число р входят и условия про екций, если они возникают в сети.
Число Гб базисных условий на единицу меньше общего чи сла исходных сторон, которое равно сумме числа k непо s
Число условий дирекционных углов на единицу меньше об щего числа kg* исходных дирекционных углов, которое равно сумме числа k непосредственно измеренных азимутов и числа a
щих одна от другой не менее чем на две определяемые из урав нивания стороны триангуляции.
Формулы (18.51) — (18.54) применяются при уравнивании триангуляции как по углам, так и по направлениям.
В качестве примера определим число независимых услов ных уравнений, возникающих в несвободной сети триангуляции (рис. 120). В этой сети число всех пунктов я = 9 ; число опреде ляемых пунктов & = 6; число всех сторон р = 17; число пунктов, на которых выполнены угловые измерения, / = 9 ; измерено: на правлений Z) = 34, базисных сторон k = 1 (ft ), азимутов k = 1 (а );
всего S = D + k + k —(2k + t) = 34 + l + l—<2×6 + 9)=l5 H 5 a
абсцисс и ординат г. = 2 ( / ^ — 1 ) = 2 ( 2 — 1 ) = 2.
В каждом геодезическом четырехугольнике с измеренными на всех его вершинах углами или направлениями возникает по четыре независимых условия: три условия фигур и одно полюс ное. В центральной системе возникает условие полюсное, ус ловие горизонта (при уравнивании углов) и условия фигур.
В данной сети (см. рис. 120) независимые условия фигур возникают: три в геодезическом четырехугольнике и по одному в остальных шести неперекрывающихся треугольниках. Полюс ные условия возникают по одному в центральной системе и в геодезическом четырехугольнике. Базисные условия возникают между исходной стороной Ь, вычисляемой по координа там исходных пунктов Л и В, и измеренной базисной стороной Ь. Условие дирекционных углов возникает между заданным 2 дирекционным углом ai исходной стороны Ь и измеренным дирекционным углом а базисной стороны Ь. Условия координат возникают между исходными пунктами В и С.
В свободной сети триангуляции исходный пункт, коорди наты которого принимают за неизменные, в число определяе мых пунктов не входит, это необходимо иметь в виду при опре делении общего числа независимых условных уравнений. В не свободной сети триангуляции всегда имеется больше одного исходного пункта с заданными (неизменными) геодезическими координатами.
При уравнивании данной сети триангуляции (см. рис. 120) по углам общее число условных уравнений найдем по формуле (18.47). В этой сети имеем: # = 26, fc =l, k = 1, & = 6. Под s a ставив эти данные в формулу (18.47), получим S = 2 6 + 1 + 1 — y —12=16. При уравнивании триангуляции по углам общее число независимых условных уравнений больше чем при уравнивании ее по направлениям, причем на число условий горизонта. В дан ной сети число условий горизонта q=N+t—Z)=26+9—34=1.
Возникает оно при полюсе центральной системы. Остальные условия те же, что и при уравнивании сети по направлениям.
§ 130. УСЛОВНЫЕ УРАВНЕНИЯ В ТРИЛАТЕРАЦИИ Общее число независимых условных уравнений в свободных и несвободных сетях трилатерации с измеренными в них дли нами сторон и азимутами ряда сторон может быть вычислено по формуле
мутов (измеренных, но не вычисленных по координатам ис ходных пунктов); k — число вновь определяемых пунктов. Сле дует подчеркнуть, что в свободной сети трилатерации исходный пункт с заданными координатами к числу определяемых пунк тов не относится.
Простейшими геометрическими фигурами в сети трилате рации, в которых возникает только по одному условному урав нению, является геодезический четырехугольник и центральная система. В треугольнике с измеренными сторонами условные уравнения не возникают, так как даже в случае грубых ошибок измерения длин сторон, например, на четверть длины, треуголь ник все равно образуется и сумма вычисленных в нем углов всегда равна точно 180°.
Число независимых условных уравнений в сети трилатера ции несравненно меньше, чем в аналогичной по схеме постро ения сети триангуляции, так как в трилатерации число избы точно измеренных величин гораздо меньше чем в триангуляции.
Например, в геодезическом четырехугольнике с измерен ными углами возникает четыре независимых условных уравне ния, а с измеренными сторонами всего лишь одно.
Виды независимых условных уравнений. В свободной сети трилатерации, имеющей один исходный пункт, измеренные длины сторон треугольников и азимуты некоторых из них мо гут возникать условные уравнения трех видов: условия геодези ческих четырехугольников, условия центральных систем и ус ловия азимутов (дирекционных углов).
В несвободной сети трилатерации могут возникать те же ус ловия, что и в свободной сети; кроме того, при наличии избы точных исходных пунктов с заданными координатами могут возникнуть условия координат (абсцисс и ординат).
Условные уравнения в сети трилатерации записывают сна чала в угловой форме (как в триангуляции), а затем поправки в углы выражают через поправки в стороны, используя диффе ренциальные формулы (18.59); наконец выполняют приведение подобных членов при одноименных поправках сторон и полу чают условные уравнения в окончательном виде. При этом по правки в длины исходных (жестких) сторон, которые не под лежат изменению, принимают равными нулю.
Условное уравнение геодезического четырехугольника с из меренными длинами сторон. Суть этого условия состоит в том, что в геодезическом четырехугольнике с вершинами /, 2, 3, 4 (рис. 121) сумма углов си и аг, вычисленных при вершине / с использованием уравненных сторон треугольников 123 и 134, должна быть равна углу аз, вычисленному по уравненным сто ронам третьего треугольника 124, т. е. должно соблюдаться ус ловие
где р » = 2 0 6 265; А/ — высота треугольника, опущенная на про тиволежащую сторону из вершины угла / ( / = Л, В, С), по правка которого определяется.
Высоты треугольника Л В С (см. рис. 122) при его вершинах вычисляют по формулам:
где п —порядковый номер последнего треугольника в цент ральной системе (в данном случае п=5).
Условия дирекционных углов. Они возникают при наличии в сети избыточного числа исходных дирекционных углов, в том числе непосредственно измеренных и вычисленных по коорди натам исходных пунктов. Условное уравнение дирекционных углов записывают сначала в угловой форме, т. е. как в триан гуляции. Затем по формулам (18.59) поправки в углы заме няют поправками в стороны, выполняют приведение подобных членов при одноименных поправках и получают условное урав нение в окончательном виде.
В качестве примера составим условное уравнение дирекци онных углов в сети (рис. 124) с заданными дирекционными уг лами ai и а. 2
с использованием измеренных сторон треугольников.
Заменив в (18.64) по формулам (18.59) поправки (С) в углы поправками (s) в стороны и приняв во внимание, что поправки (Ь) и (Ь ) в исходные стороны Ь и Ь равны нулю,
(18.65) Базисные условия в сетях трилатерации не возникают, так как ко всем непосредственно измеренным сторонам треуголь ников определяются поправки из уравнивания, в результате чего данные условия автоматически выполняются.
Условия координат (абсцисс и ординат) возникают в тех ж е случаях, как в триангуляции, когда имеются раздельные группы исходных пунктов, удаленные одна от другой не менее чем на две измеренные стороны. Координатные условия запи сывают сначала в угловой форме (как в триангуляции при уравнивании ее по углам), а затем поправки углов треугольни ков выражают через поправки к длинам сторон и получают в окончательном виде эти уравнения.
Число независимых условных уравнений Общее число S независимых условных уравнений в сети трила терации находят по формуле (18.55):
S = N + k —2k. a Число с условных уравнений геодезических четырехуголь ников и уравнений центральных систем вместе взятых равно числу избыточных сторон в сети, т. е.
с= р—2м+3, где р — число всех сторон (исходных и измеренных), п — чи сло всех пунктов в сети (исходных и определяемых).
Число r условий дирекционных углов определяется по фор g
ных одна от другой не менее чем на две измеренные (не вы численные по координатам) стороны.
§ 131. ОПРЕДЕЛЕНИЕ ДОПУСТИМЫХ ЗНАЧЕНИЙ
Видео:Подготовка измерений к уравниванию или предобработка. Основные теоретические моменты.Скачать

СВОБОДНЫХ ЧЛЕНОВ УСЛОВНЫХ УРАВНЕНИИ
Прежде чем приступить к уравниванию геодезической сети (триангуляции, трилатерации, линейно-угловой и т. п.) необ ходимо убедиться, что измерения в ней выполнены качест венно и по точности удовлетворяют предъявляемым к ним требованиям. Д л я этого вычисляют свободные члены всех без исключения условных уравнений (зависимых и независимых) и сравнивают их значения с установленными допусками.
Получим сначала общую формулу для расчета допустимой величины свободных членов условных уравнений.
Условное уравнение любого вида запишем в общем виде а Л + я ^ 2 +. •.+a v + (o = 0. (18.66) n n
где параметр t зависит от доверительной вероятности, а следо вательно, и от числа п измерений (числа невязок со однород ных условных уравнений в сети); ошибка i устанавливается действующими инструкциями для каждого вида измерений и в зависимости от класса геодезической сети.
Ряды измерений, по которым оценивают параметр t могут быть разными по величине. Так, например, число треугольни ков, для которых устанавливается предельная величина не вязки, в одной сети может быть порядка 10—15, а в другой гораздо больше — порядка 200 и более.
11 17 2,71 2,17 75 2,00 2,39 13 2,07 2,24 20 2,49 2,81 15 2,13 3,02 25 2,33 50 2,58 200 Параметр / при таких значениях п согласно приближенному критерию Шовенэ находится в интервале 2,0—3,0 (табл. 48).
В современных инструкциях по построению государствен ных геодезических сетей принято в среднем / = 2,5.
Ниже даны формулы для вычисления предельных значений свободных членов конкретных условных уравнений.
В формулах (18.68—18.73) приняты следующие обозначе ния: т» — средняя квадратическая ошибка измерения углов;
п — число углов в условном уравнении; S c t g p — сумма квад ратов котангенсов связующих углов в условном уравнении;
Ь и & — длины начальной и конечной базисных (исходных) 2
дирекционных углов си и а в условном уравнении; р » = 206 265;2 [ a ^ ] и [flj/ay] — суммы квадратов коэффициентов при по правках (Л), ( 5 ), (С) в углы в условных уравнениях абсцисс и ординат соответственно; т. и т.— средние квадратические х у ошибки абсцисс и ординат исходных пунктов.
где k — число условных уравнений центральных систем и ус ловных уравнений геодезических четырехугольников вместе взятых; ©г — свободные члены условных уравнений; — суммы квадратов коэффициентов при поправках (s) в измерен ные длины сторон в этих уравнениях; следует отметить, что ошибка т- относится к сторонам средней длины, т. е. к S = 2S/M.
2. Условия дирекционных углов
где [Кк]—сумма квадратов коэффициентов в условном урав нении (18.65) при поправках (s) в измеренные длины сторон;
т — — с р е д н я я величина средней квадратической ошибки изме рения сторон в сети трилатерации; m и — средние квадра ttl тические ошибки исходных дирекционных углов си и С&2.
3. Условия абсцисс и ординат
ние квадратические ошибки координат исходных пунктов.
Если свободные члены каких-либо условных уравнений пре вышают установленные допуски, необходимо выявить причины этих отклонений и устранить их.
Видео:Самый простой способ решить кубическое уравнениеСкачать

§ 132. ПОСЛЕДОВАТЕЛЬНОСТЬ УРАВНИТЕЛЬНЫХ ВЫЧИСЛЕНИИ.
Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

ОЦЕНКА ТОЧНОСТИ
Оценка точности функций уравненных элементов. В том случае, когда требуется вычислить среднюю квадратическую ошибку какого-либо уравненного элемента F геодезической сети, например, ошибку дирекционного угла а или длины 5 какой-либо стороны, сначала следует представить этот элемент F как функцию уравненных величин. Затем надо получить при ращение AF, т. е. составить весовую функцию для оценивае мого элемента ( A F = / ; A!F = f ). Весовую функцию f (f ) за a 8 a 8
где средняя квадратическая ошибка единицы веса v — поправки из уравнения в измеренные с весами р вели чины; г — число условных уравнений, равное числу избыточных измерений в сети.
Примеры уравнивания сетей триангуляции и трилатерации коррелатным способом, включая оценку точности уравненных элементов, даны в Практикуме по высшей геодезии [23].
Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ
Видео:Уравнивание нивелирных сетей параметрическим методом.Скачать

ПАРАМЕТРИЧЕСКИМ СПОСОБОМ
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

§ 133. ПОСЛЕДОВАТЕЛЬНОСТЬ УРАВНИТЕЛЬНЫХ ВЫЧИСЛЕНИИ.
Видео:Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать

СООТНОШЕНИЕ ВЕСОВ ИЗМЕРЕННЫХ ВЕЛИЧИН
В связи с широким внедрением ЭВМ в геодезическое произ водство параметрический способ уравнивания геодезических се тей стал преобладающим, поскольку линейные уравнения по правок, составляемые на пунктах сети, имеют одинаковую структуру. Это дает возможность составлять универсальные программы уравнивания на ЭВМ геодезических сетей, в том числе триангуляции, трилатерации, линейно-угловых, комбини рованных и т. п. При параметрическом способе задача уравни 2 вания решается под тем же условием 2 pu = min, что и при ис пользовании коррелатного способа.
Д л я параметрического способа уравнивания характерна сле дующая последовательность уравнительных вычислений. Сна чала с возможно большей точностью решают треугольники, оп ределяя в сети триангуляции длины сторон, а в сети трилате рации углы треугольников. Затем, также с возможно большей точностью, вычисляют координаты всех определяемых пунктов.
Далее, используя полученные координаты, по всем сторонам сети решают обратные геодезические задачи и с высокой точ ностью находят длины и дирекционные углы сторон, соответ ствующие этим координатам, включая и координаты исходных пунктов. На следующем этапе вычислений составляют уравнемия поправок для всех непосредственно измеренных величин:
горизонтальных направлений, измеренных азимутов (дирекци онных углов), измеренных расстояний между пунктами. Вес каждого измеренного элемента принимают равным в общем 2 случае р = с/пг. От уравнений поправок с учетом весов переходят к системе нормальных уравнений, из решения которых находят поправки в приближенные координаты определяемых пунктов. Затем вычисляют уравненные координаты пунктов и выполняют контрольные вычисления, исправив предварительно измеренные величины поправками, полученными из уравнива ния. Наконец, выполняют оценку точности уравненных элемен тов сети.
При уравнивании геодезических сетей с разнородным соста вом измерений (углов, азимутов, длин сторон и т. п.) одним из наиболее ответственных и сложных вопросов является установ ление точного соотношения весов всех измеренных в сети ве личин. В общем случае вес измеренной величины вычисляется по формуле р_ с _ у?
tnj ntj где i — средняя квадратическая ошибка единицы веса; пг,— средняя квадратическая ошибка измерения /-ой величины. Вы 2 бор постоянной с = р, до некоторой степени произволен и опре деляется удобствами вычислений. Приняв
где m — средняя квадратическая ошибка измеренного направ N ления, получим следующие формулы для вычисления весов из меренных направлений N, азимутов а и длин сторон s:
От того, насколько достоверно будет установлено соотноше ние эмпирических дисперсий т,, т и т, зависит достоверность результатов уравнивания геодезической сети. При этом следует иметь в виду то, что средние квадратические ошибки m дол жны быть определены не по внутренней сходимости результа тов измерений в приемах, а с учетом совместного влияния как случайных так и систематических ошибок. Наиболее надежные оценки ошибок получают по свободным членам соответствую щих условных уравнений.
В сетях триангуляции среднюю квадратическую ошибку
В сетях трилатерации среднюю величину средней квадрати ческой ошибки измерения сторон можно определить по свобод ным членам большого числа условных уравнений геодезических четырехугольников и центральных систем
ратов коэффициентов условного уравнения i-й центральной системы или геодезического четырехугольника; k — число сво бодных членов со/.
Практика астрономо-геодезических работ показывает, что средняя квадратическая ошибка определения азимутов на пунктах Лапласа, вычисленная по расхождениям большого чи сла взаимно обратных азимутов, достаточно близка к реальной величине. Чаще оценку их точности выполняют по расхожде ниям результатов измерений в приемах и получают значи тельно преуменьшенную (в 2—3 раза) ошибку по сравнению с ее реальной величиной (—1,1—1,2″).
Следует еще раз подчеркнуть, что при уравнивании геоде зических сетей поправки необходимо определять во все непос редственно измеренные величины: направления, азимуты и длины сторон, причем с учетом их действительных весов, опре делению которых надлежит уделять самое серьезное внимание.
Гаусса-Крюгера, относительно которого отсчитываются дирекционные углы а^. Прове дем направление iO, совпа дающее с нулевым диаметром лимба, относительно которого отсчитываются значения изме ренных направлений на пун кте. Обозначим z угол между направлением ix и направле нием Ю нулевого диаметра лимба. Угол z принято назы вать ориентирующим К у г л о м, поскольку он ориен тирует измеренные на пункте направления относительно осевого меридиана зоны проекции Гаусса — Крюгера.
Д л я любого измеренного на пункте направления ik примем следующие обозначения:
3 aik — приближенное значение дирекционного угла, вычис ленное по координатам пунктов;
Aaik — поправка в дирекционный угол из уравнивания;
— уравненный дирекционный угол;
oLik = oiik+aik Nk —измеренное направление, отсчитываемое от нулевого диаметра лимба;
Vik — поправка в направление из уравнивания;
Nik = N,ik + Vik — уравненное направление.
2 — приближенное значение ориентирующего угла на 0
Уравнения поправок измеренных сторон В геодезической сети могут быть измерены как базисные (с по вышенной точностью), так и другие стороны, как например, в сети трилатерации и полигонометрии. Во все стороны, реду цированные на плоскость, определяют поправки из уравнива ния, причем с учетом весов измерений.
Используя измеренные стороны, углы и т. п. решают тре угольники и затем вычисляют приближенные координаты пунктов с возможно большей точностью. Из решения обратных задач находят длины s ° всех измеренных сторон, строго соот ih ветствующие этим координатам:
Уравнение поправок (19.29) соответствует общему случаю, когда сторона s измерена между определяемыми пунктами.
В частных случаях уравнение (19.29) принимает более простой вид, например, если сторона измерена между исходным пунктом i(li = ri = 0) и определяемым пунктом k
§ 135. СОСТАВЛЕНИЕ РЕДУЦИРОВАННЫХ
Видео:Как решать уравнения с дробью? #shortsСкачать

НОРМАЛЬНЫХ УРАВНЕНИИ
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

НА ПУНКТАХ ТРИАНГУЛЯЦИИ И ПОЛИГОНОМЕТРИИ
Поскольку при уравнивании сети по направлениям на каждом пункте триангуляции и полигонометрии сумма поправок Vik в измеренные направления равна нулю ( [ i ] = 0 ), то можно составить так называемые р е д у ц и р о в а н н ы е н о р м а л ь н ы е у р а в н е н и я, в которых поправки б z в ориентирую 0
(19.38) равное сумме уравнений (19.33); 3) присоединить это уравне ние к системе начальных уравнений (19.33) с фиктивным ве сом р = — l / / i, где п — число направлений на пункте; 4) счи тать условно, что в уравнениях (19.33) и (19.38) поправка 6 z 0
к нормальным уравнениям. В итоге будут получены редуциро ванные нормальные уравнения (19.37).
Д л я того чтобы убедиться в этом, вычислим, например, квадратичный коэффициент при первом неизвестном /:
которых выполнены угловые измерения.
§ 136. ВЫЧИСЛЕНИЕ УРАВНЕННЫХ ЭЛЕМЕНТОВ СЕТИ.
Видео:Иррациональное уравнениеСкачать

ОЦЕНКА ТОЧНОСТИ
Будем полагать, что на предыдущей стадии вычислений состав лены уравнения поправок для всех измеренных в сети величин:
горизонтальных направлений, дирекционных углов, длин сто рон и что вес pi каждого i-ro уравнения (измеренной величины) известен. Пусть А — прямоугольная матрица коэффициентов уравнений поправок, включая суммарные уравнения на пунк тах с измеренными углами; X — вектор-столбец поправок и т|г в приближенные координаты определяемых пунктов; / — вектор-столбец свободных членов U уравнений поправок; Р — диагональная матрица весов pi уравнений поправок.
Используя эти обозначения, запишем все уравнения попра вок в матричной форме
N — симметричная матрица коэффициентов нормальных урав т нений; А — транспортированная матрица А; Р — диагональ ная матрица весов уравнений поправок; L — вектор-столбец свободных членов нормальных уравнений.
Умножив каждое слагаемое уравнения (19.40) слева на матрицу Л Н, обратную матрице N коэффициентов нормальных уравнений, найдем вектор X искомых поправок координат
Координаты пунктов, вычисленные по формулам (19.45), оп ределены бесконтрольно. Д л я контроля и получения уравнен ных значений измеренных величин поступают следующим об разом. Найденные из решения системы нормальных уравнений поправки г и т]г подставляют в соответствующие уравнения по правок (19.38), (19.9), (19.19), (19.29) и находят значения самих поправок 6z, v, v, v. Введя поправки в измерен 0 N т aт s <ik) ные величины, получают их уравненные значения:
В полигонометрии координаты по формулам (19.47) вычис ляют без двойного контроля, т. е. по одной из этих формул.
Заключительным контролем правильности уравнительных вычислений является совпадение координат, вычисленных для каждого пункта дважды, т. е. по формулам (19.45) и (19.47).
Расхождения не должны выходить за пределы ошибок округ лений.
Оценка точности уравненных элементов сети Среднюю квадратическую ошибку единицы веса находят по формуле (19.48) где v — поправки из уравнивания в измеренные с весами р ве личины; г — число избыточных измерений в сети, определяемое как разность числа всех k измерений в сети и числа k неиз 0
Число k равно сумме измеренных направлений на всех пунк тах, измеренных азимутов земных предметов и измеренных сторон, в которые находят поправки из уравнивания.
В число k входят поправки 6z в ориентирующие углы на пунктах триангуляции и полигонометрии, а также поправки 6х и 8у в приближенные координаты определяемых пунктов. Чи сло поправок б 2 равно числу пунктов, на которых выполнены 0 угловые измерения (исходные и определяемые); число поправок дх и 6у равно удвоенному числу определяемых пунктов.
Среднюю квадратическую ошибку любой функции F урав ненных элементов (дирекционных углов, длин сторон, абсцисс и ординат) вычисляют по формуле
Обратный вес 1/PF оцениваемой функции F может быть вы числен по-разному: в процессе решения системы нормальных уравнений по схеме Гаусса или по элементам матрицы, обрат ной матрице коэффициентов нормальных уравнений. Рассмот рим сначала первый способ вычисления обратного веса функции.
При параметрическом способе уравнивания наиболее просто вычисляется вес последнего и предпоследнего неизвестных в системе нормальных уравнений. Поэтому чтобы определить вес Р и Р координат какого-либо пункта k, неизвестные х Ук
где С и А — квадратичные коэффициенты соответственно по следнего и предпоследнего преобразованных нормальных урав нений; В— коэффициент при щ в предпоследнем преобразован ном уравнении.
Д л я того чтобы найти среднюю квадратическую ошибку любого элемента уравненной сети, являющегося функцией ко ординат пунктов, например, длины и дирекционного угла сто роны между любыми пунктами (смежными или несмежными), этот элемент следует выразить через координаты этих пунктов, а затем составить весовую функцию.
Получим весовую функцию для оценки произвольной сто роны sat, длину которой представим как А = У(**—**) + (Ук—yif Продифференцировав это выражение по координатам определяемых пунктов и перейдя от дифференциалов к конечным величинам, найдем приращение данной функции
где коэффициенты а^, bih вычисляются по формулам (19.11).
В общей системе нормальных уравнений после графы L свободных членов вводят дополнительные графы коэффициен тов функций f и f в уравнениях с квадратичными коэффициен s a
вычисляют одновременно с решением нормальных уравнений.
Их величины находят как суммы произведений чисел, записан ных в элиминационных сторонах столбца (графы) на соответ ствующие числа этого ж е столбца преобразованных нормаль ных уравнений.
Во втором случае, когда система нормальных уравнений ре шается с вычислением обратной матрицы Q = N
обратный вес уравненных абсцисс х и ординат у равен диагональным элементам обратной матрицы Q, т. е.
(19.52) и (19.53) соответственно.
Заключительным этапом уравнительных вычислений явля ется составление каталога координат пунктов, в котором длины сторон и дирекционные углы вычисляют путем решения обрат ных задач с использованием координат, записанных в каталог.
Примеры уравнивания геодезических сетей, в том числе триангуляции, трилатерации и линейно-угловых параметриче ским способом даны в Практикуме по высшей геодезии [23].
1. Баранов В. И., Бойко Е. Г., Краснорылов И. Я. и др. Космическая геодезия.— М.: Недра, 1986.
2. Большаков В. Д., Гайдаев Я. А. Теория математической обработки геодезических измерений.— М.: Недра, 1977.
3. Большаков В. Д., Деймлих Ф., Голубев А. Н., Васильев В. Я. Радио геодезические и электрооптические измерения.— М.: Недра, 1985.
4. Вировец А. М. Высшая геодезия.— М.: Недра, 1970.
5. Гайдаев П. А. Математическая обработка геодезических сетей.—М.:
6. Дурнев А. И. Высшая геодезия.— М.: Недра, 1967.
7. Закатов Я. С. Курс высшей геодезии.—М.: Недра, 1976.
8. Инструкция о построении государственной геодезической сети СССР — М.: Недра, 1966.
9. Инструкция по полигонометрии и трилатерации.— М.: Недра, 1976.
10. Инструкция по нивелированию I, I I, I I I и I V классов.— М.: Недра, 1974.
И. Инструкция по вычислению нивелировок.— М.: Недра, 1971.
12. Конопальцев И. М. Высокоточные угловые измерения при изучении движений земной коры.— М.: Недра, 1978.
13. Кочетов Ф. Г. Нивелиры с компенсаторами.— М.: Недра, 1985.
14. Красовский Ф. Н. Избранные сочинения, т. I I I. — М. : Геодезиздат, 1955.
15. Кузнецов Я. Я., Васютинский И. Ю., Ямбаев X. К. Геодезическое инструментоведение.— М. : Недра, 1984.
16. Машимов М. М. Уравнивание геодезических сетей.— М.: Недра, 1989.
17. Нивелирование I и II классов: Практическое руководство,— М. :
18. Огородова Л. В., Шимбирев Б. П., Юзефович А. Я. Гравиметрия.— М.: Недра, 1978.
19. О нивелирной сети СССР/Под общей редакцией Л. А. Кашина и Л. С. Хренова.—М.: Недра, 1979.
20. Павлив Я. В. Проблемы высокоточного нивелирования.— Львов: Из дательство ЛГУ, 1980.
21. Пеллинен Л. П. Высшая геодезия — М. : Недра, 1978.
22. Плотников В. С. Геодезические приборы.— М.: Недра, 1987.
23. Практикум по высшей геодезии/Под редакцией Н. В. Яковлева —М.:
24. Руководящий технический материал. Определение азимутов на пунктах Лапласа с учетом влияния рефракции. ГУГК при СМ СССР — М. :
25. Спиридонов А. И. Теодолиты.—М.: Недра, 1985.
26. Справочник геодезиста/Поя редакцией В. Д. Большакова и Г. П. Левчука.—М.: Недра, 1985, Предметный указатель
Яковлев Николай Васильевич
Видео:Решение прямой геодезической задачиСкачать

ВЫСШАЯ ГЕОДЕЗИЯ
Заведующий редакцией Л. Г. Иванова Редактор издательства Ю. В. Пронько Технический редактор Е. С. Сычева Корректор Л. В. Зайцева ИБ № 6773
Ордена «Знак Почета» издательство «Недра», 125047 М о с к в а, пл. Белорусского вок з а л а, 3.
Ленинградская типография № 4 ордена Трудового Красного Знамени Ленинградского о б ъ е д и н е н и я « Т е х н и ч е с к а я книга» и м. Евгении С о к о л о в о й Г о с у д а р с т в е н н о г о к о м и т е т а С С С Р по печати. 191126, Л е н и н г р а д, С о ц и а л и с т и ч е с к а я у л., 14.
Видео:СОСТАВНЫЕ УРАВНЕНИЯ / Математика 3 ,4 класс Петерсон , Моро . Как научить решать составные уравненияСкачать

ВНИМАНИЮ НАУЧНЫХ
Видео:Как решают уравнения в России и США!?Скачать

И ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ
РАБОТНИКОВ, АСПИРАНТОВ
В издательстве «Недра» готовятся к выпуску
СПРАВОЧНЫЕ П О С О Б И Я,
содержащие полную информацию по геодезии и картографии, другим смежным отраслям науки и производства.
В авторский коллектив входят руководители ГУГК С С С Р, уче ные, представляющие различные научные школы, а также опыт ные производственники.
Серия справочных пособий по теории и практике геодезии впервые выпускалась в 1939 г. под общей редакцией М. Д. БончБруевича издательством Наркомзема Р С Ф С Р.
Настоящее издание отражает современное состояние геоде зии и картографии, новейшие достижения в этих областях.
Если Вас заинтересовали книги издательства «Недра», реко мендуем Вам оформить предварительный заказ в магазинах, распространяющих научно-техническую литературу.
СВОЕВРЕМЕННО ОФОРМЛЕННЫЙ ЗАКАЗ
ГАРАНТИРУЕТ ПРИОБРЕТЕНИЕ
НУЖНОЙ ВАМ КНИГИ.
АДРЕСА ОПОРНЫХ МАГАЗИНОВ
ИЗДАТЕЛЬСТВА «НЕДРА»
199178 ЛЕНИНГРАД, В. О., СРЕДНИЙ ПРОСПЕКТ, 61, М А Г А З И Н № 17 «НЕДРА»




















2016 www.metodichka.x-pdf.ru — «Бесплатная электронная библиотека — Методички, методические указания, пособия»
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.