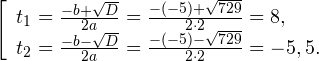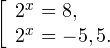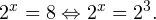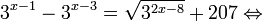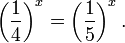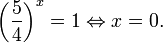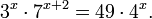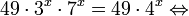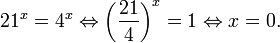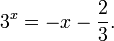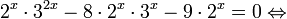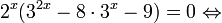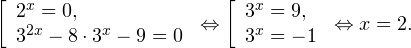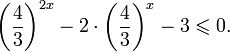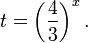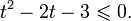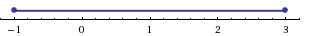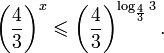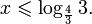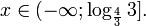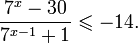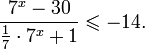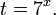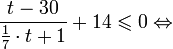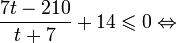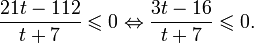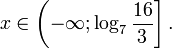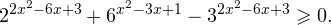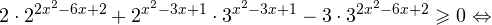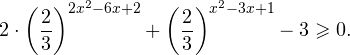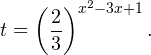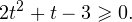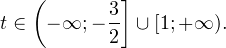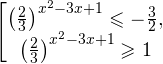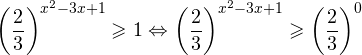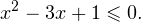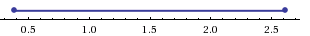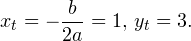Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
ФИПИ База «Показательные неравенства» Алгебра 10 класс
Задание 1.1
Задание 1.2
Задание 1.3
Задание 2.1
Задание 2.2
Задание 3.2
Задание 4.1
Задание 4.2
Задание 5.1 

Задание 6.1
Задание 6.2
Курс профессиональной переподготовки
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Показательные неравенства на ЕГЭ по математике
- Показательные уравнения и неравенства
- Показательная функция
- Что такое показательная функция?
- Решение показательных неравенств
- 🎬 Видео
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 693 человека из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 859 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 49 человек из 21 региона
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Показательные уравнения. 11 класс.Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 842 395 материалов в базе
Материал подходит для УМК
«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
§ 13. Показательные неравенства
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 20.12.2020
- 168
- 2
- 20.12.2020
- 138
- 5
- 20.12.2020
- 79
- 3
- 20.12.2020
- 965
- 88
- 20.12.2020
- 78
- 0
- 20.12.2020
- 297
- 2
- 20.12.2020
- 142
- 4
- 20.12.2020
- 457
- 10
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 20.12.2020 797
- DOCX 530.3 кбайт
- 90 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Чистякова Елена Аркадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 7 месяцев
- Подписчики: 0
- Всего просмотров: 2068
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Старт Щелчка. №14 Неравенства с нуля и до ЕГЭ за 5 часов | Логарифмы, степени для №5,6,12Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
В Госдуме предложили унифицировать школьные программы
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Онлайн-конференция о профессиональном имидже педагога
Время чтения: 2 минуты
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Показательные неравенства на ЕГЭ по математике
Знакомство с этой темой мы начнем с самых простых показательных неравенств.
Так же, как и при решении простейших показательных уравнений, представим правую часть в виде степени числа 2:
Когда я спрашиваю школьников, что делать дальше, они обычно отвечают: «Убрать основания!» Я не против такой формулировки, просто надо четко представлять себе, почему мы так делаем. А для этого — вспомним, как выглядит график показательной функции y = 2 x .

Видим, что эта функция монотонно возрастает, то есть большему значению x отвечает большее значение y. И наоборот, если 2 x1 > 2 x2 , то x1 > x2 . Итак, от неравенства 2 x > 2 3 можно перейти к алгебраическому неравенству x > 3.
2. Следующее неравенство:
Так же, как и в предыдущем примере, представим правую часть в виде значения показательной функции. Как это сделать? С помощью логарифма, конечно:
7 = 2 log27 .
3. Еще одно неравенство:
Здесь правую часть удобно представить как .
Вспомним, как выглядит график функции :
Эта функция монотонно убывает (так как основание степени меньше единицы), поэтому большее значение функции соответствует меньшему значению аргумента. То есть из неравенства left ( frac right )^» src=»https://latex.codecogs.com/png.latex?%5Cleft&space;(&space;%5Cfrac%3C1%3E%3C2%3E&space;%5Cright&space;)%5E%3Cx%3E&space;%3E&space;%5Cleft&space;(&space;%5Cfrac%3C1%3E%3C2%3E&space;%5Cright&space;)%5E%3C4%3E» /> следует, что x x − 2 · 5 2x − 10 x > 0.
Заметим, что 4 x = 2 2x , 10 x =5 x ·2 x , и запишем неравенство в виде:
2 2x − 5 x ·2 x − 2 · 5 2x > 0.
Разделим обе части на положительную величину 5 2x и обозначим . Получим квадратное неравенство:
Кроме того, t > 0.
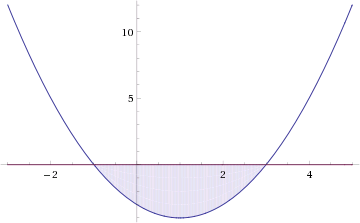
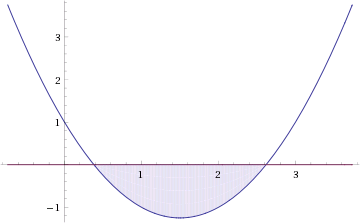
Графиком функции y = t 2 − t − 2 является парабола, ветви которой направлены вверх. Решая квадратное уравнение t 2 − t − 2 = 0, получим t1 = −1, t2 = 2. В этих точках наша парабола пересекает ось t. 
Отметим на числовой прямой промежутки, являющиеся решениями неравенств t 2 − t − 2 > 0 и t > 0. 
Видим, что обоим неравенствам удовлетворяют значения t > 2.
Но решение еще не закончено! Нам нужно вернуться к переменной x. Вспомним, что и получим:
Представим 2 в виде степени с основанием :
Его дискриминант , корни
Объединяем решения обоих систем на числовой прямой.
Получаем, что значит,
Каким бы ни было показательное неравенство — его надо упростить до неравенства Знак здесь может быть любой: . Важно, чтобы слева и справа в неравенстве находились степени с одинаковыми основаниями.
И после этого «отбрасываем» основания! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что , знак неравенства меняется на противоположный.
Видео:ЗАДАНИЕ 8 ЕГЭ (ПРОФИЛЬ). ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВАСкачать

Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Видео:Показательные неравенства. 11 класс.Скачать

Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен:
Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решите уравнение: Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать  Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решите неравенство: Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: Воспользуемся заменой переменной: Исходное уравнение тогда принимает вид: Итак, неравенству удовлетворяют значения t, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству: Итак, окончательный ответ: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. 🎬 ВидеоПоказательные неравенства за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать  Это просто! Как решать Показательные Неравенства?Скачать  Показательные уравнения. Задание 13 | Математика ЕГЭ | УмскулСкачать  Разбор досрочного варианта | Базовая математика ЕГЭ 2023 | УмскулСкачать  ВСЕ ТИПЫ заданий №16 на ЕГЭ | Базовая математика ЕГЭ 2023 | УмскулСкачать  ЕГЭ по математике изменили | ЕГЭ 2024 будет сложнее?Скачать  ✓ Показательное уравнение | ЕГЭ-2017. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать  Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать  ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать  Задание 18 | ЕГЭ 2024 Математика (база) | НеравенстваСкачать  Показательные уравнения за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать  ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ НА ЕГЭ | Решаем №12 из профильной математикиСкачать  Показательные уравнения и неравенстваСкачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  |
























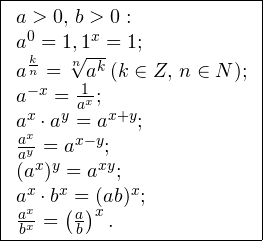 0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n]
0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n] 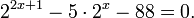
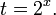
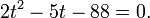
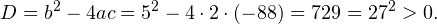 0. ]» title=»Rendered by QuickLaTeX.com»/>
0. ]» title=»Rendered by QuickLaTeX.com»/>