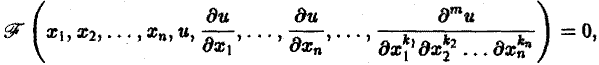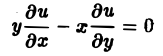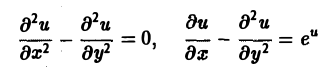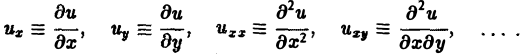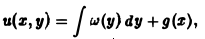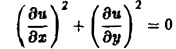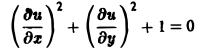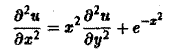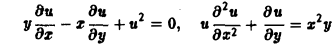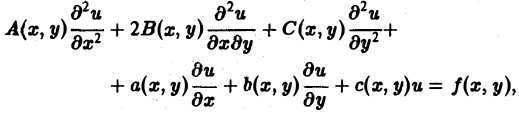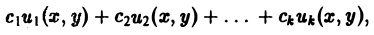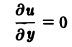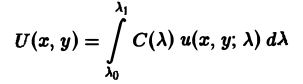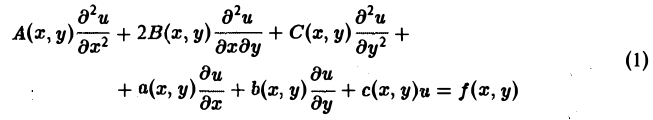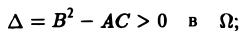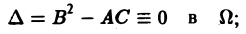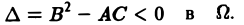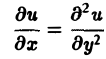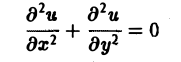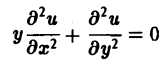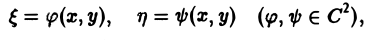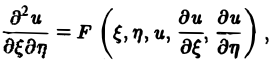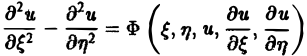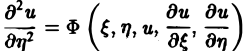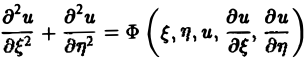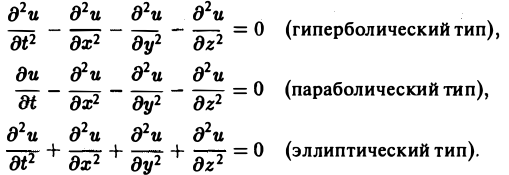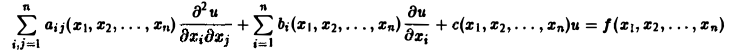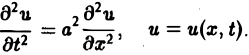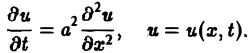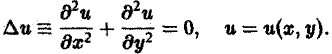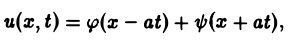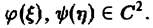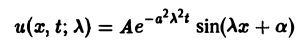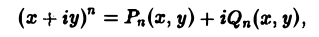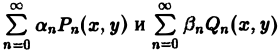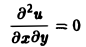Показать что функция удовлетворяет дифференциальному уравнению в частных производных

Видео:показать, что функция удовлетворяет соотношениюСкачать

Примеры по дифференциальным уравнениям в частных производных

Видео:21. Частные производные второго порядка. Часть 4.Скачать

Немного теории

Дифференциальным уравнением с частными производными (ДУ с ЧП) называется уравнение относительно неизвестной функции нескольких переменных (ФНП) и ее частных производных. Наивысший порядок частных производных (существенно входящих в уравнение) называется порядком этого уравнения.

ДУ с ЧП называется линейным (ЛДУ с ЧП), если неизвестная функция и ее производные входят в это ДУ линейно (в первой степени).

В этом разделе вы найдете подробно решенные задачи по темам: классификация и приведение к каноническому виду ДУ с ЧП второго порядка с двумя переменными, определение типа уравнения, решение уравнений и систем ДУ в ЧП.

ДУ с ЧП находят широкое применение в прикладных науках: квантовая механика, электродинамика, термодинамика, теория теплои массопереноса и др. при математическом описании и моделировании различных физических процессов. Поэтому такие уравнения изучаются под общим названием уравнений математической физики (примеры решений 16 задач).

Видео:Частные производные функции многих переменныхСкачать

Приведение к каноническому виду

Задача 1. Привести к каноническому виду уравнение

Задача 2. Привести уравнение к каноническому виду.

Задача 3. Найти общее решение уравнения, приведя его к каноническому виду:

Видео:27. Дифференцирование неявной функции двух переменныхСкачать

Решение ДУ в ЧП

Задача 4. Решить уравнение Пфаффа

$$ z^2 dx +zdy +(3zx +2y)dz=0. $$

Задача 5. Решить задачу Коши для уравнения в частных производных

$$ u_-2Delta u =(x^2+y^2+z^2)t; quad u(t=0)=xyz, u_t(t=0)=x-y. $$

Задача 6. Найти общее решение уравнения в частных производных

Задача 7. Найти общее решение уравнения в частных производных первого порядка.

$$ xy u_x +(x-2u)u_y = yu. $$

Задача 8. Найти решение задачи Коши для уравнения в частных производных

$$ y u_x -xy u_y=2xu, quad u(x+y=2)=1/y. $$

Задача 9. Решить систему дифференциальных уравнений в частных производных

Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

Разные задачи на исследование ДУ в ЧП

Задача 10. Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию

Задача 11. Найти области гиперболичности, эллиптичности и параболичности уравнения и исследовать их зависимость от $l$, где $l$ – числовой параметр.

Задача 12. Найти функцию, гармоническую внутри круга радиуса $R$ c центром в начале координат и такую, что

Видео:Линейные дифференциальные уравнения в частных производныхСкачать

Помощь с решением ДУ в ЧП

Если вам нужна помощь с решением задач и контрольных по дифференциальным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Видео:Уравнения в частных производных 1Скачать

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

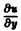
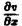
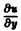
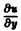
Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 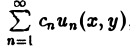, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Видео:6. Линейные однородные уравнения в частных производных первого порядкаСкачать

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 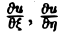и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 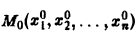и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 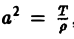где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 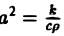где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

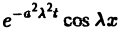
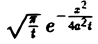
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:1. Что такое дифференциальное уравнение?Скачать

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Видео:Показать, что неявная функция удовлетворяет соотношениюСкачать

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Видео:Горицкий А. Ю. - Уравнения математической физики - Уравнения с частными производными 1-го порядкаСкачать

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]" title="Rendered by QuickLaTeX.com" />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

🔍 Видео

Сергеев И. Н. - Дифференциальные уравнения II - Уравнения в частных производных первого порядкаСкачать

Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения для самых маленькихСкачать

Найти общее решение уравнения в частных производных первого порядка.Скачать