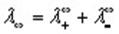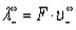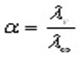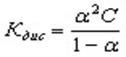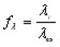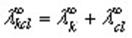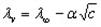Эквивалентная электропроводность при бесконечном разбавлении как для сильных, так и для слабых электролитов может быть вычислена с помощью закона Кольрауша.
Согласно закону Кольрауша эквивалентная электропроводность раствора электролита при бесконечном разбавлении определяется выражением:
где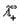 
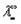
и 
—эквивалентные электропроводности катионов и анионов при бесконечном разбавлении.
Эквивалентные электропроводности ионов называются также подвижностями. Они равны произведению абсолютной скорости ионов на число Фарадея, т.е.
и 
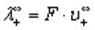
где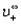 
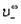
и 
— абсолютные скорости катионов и анионов при бесконечном разбавлении.
По измеренным сопротивлениям для каждой из концентраций вычисляют удельную электропроводность, эквивалентную электропроводность, а затем вычисляют степень диссоциации по уравнению:
— вычисляют по закону Кольрауша
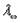
Константу равновесия процесса диссоциации слабого электролита вычисляют по уравнению (закон разбавления Оствальда):
где ? – степень диссоциации,
С – концентрация раствора.
При работе с раствором сильного электролита необходимо вычислить коэффициент электропроводности по уравнению:
— электролита вычисляется по закону Кольрауша:
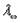
Подвижности ионов К’ и Cl’ взять из приложения ( в конце работы).
Для сильных электролитов зависимость эквивалентной электропроводности от концентрации выражается эмпирическим уравнением Кольрауша
где а – постоянная, зависящая от природы электролита, растворителя и температуры.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать
Абсолютная скорость движения ионов (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Все ткани организма пропитаны и омываются биологическими жидкостями, в которых растворены сильные и слабые электролиты. Поэтому такие биологические жидкости как кровь, лимфа, спинномозговая жидкость, слезная жидкость, слюна и т. д. относятся к проводникам второго рода.
Абсолютная скорость движения ионов. В растворах электролитов сольватированные ионы находятся в беспорядочном движении. При наложении электрического поля возникает упорядоченное движение ионов к противоположно заряженным электродам.
Сравнение скоростей движения различных видов ионов производят при градиенте потенциала поля 1 В/м. Для этих условий скорость движения ионов называют абсолютной, обозначают буквой w и выражают в м2 × B–1 × c–1. Абсолютная скорость движения иона –– это расстояние в метрах, которое проходит ион за 1 с при градиенте потенциала 1В/м. Численные значения абсолютных скоростей движения ионов в данном растворителе зависят только от их природы и температуры.
Для оценки способности ионов к перемещению под действием внешнего поля пользуются также количественной характеристикой – подвижность ионов (U). Подвижность иона представляет собой произведение числа Фарадея (F = 96465 B × с × См × моль–1) на абсолютную скорость движения иона и выражается в См × м2 × моль–1:
Значения абсолютных скоростей движения и подвижностей ионов при 250С представлены в таблице 1:
Таблица 1
Из приведенных в табл.1 данных можно усмотреть некоторые закономерности. Во-первых, абсолютная скорость движения катионов растет в пределах одной группы периодической системы элементов с ростом порядкового номера, как это видно из данных для катионов щелочных металлов. Сравнение расположенных в одном периоде и имеющих приблизительно одинаковый размер ионов Na+, Mg2+, Al3+ показывает незначительное увеличение абсолютной скорости движения с увеличением заряда иона. Оба эти факта объясняются явлением сольватации ионов в растворе. Молекулы растворителя группируются вокруг иона и увеличивают его эффективный радиус (который называется гидродинамическим радиусом).
В электрическом поле в растворах электролитов перемещается не свободный ион, а ион с плотно связанной с ним сольватной оболочкой. В силу меньшего размера ион Li+ сильнее притягивает диполи воды и в итоге имеет большую сольватную оболочку, чем ион калия. Следовательно, небольшие ионы имеют больший гидродинамический радиус и характеризуются меньшей абсолютной скоростью движения. Этим же объясняется малое отличие в абсолютной скорости движения ионов Na+, Mg2+, Al3+. С увеличением заряда, естественно, резко возрастает сольватная оболочка и тем самым размер перемещающейся частицы. Это увеличение размера почти полностью компенсирует эффект увеличения заряда.
Обращает также на себя внимание аномально высокая абсолютная скорость движения ионов гидроксония H 3 O + ( H + ) и гидроксила OH – . Можно предположить, что ион Н+ должен быть сильно сольватирован, тем не менее он способен быстро передвигаться в растворе. В этом случае нельзя применить гидродинамический довод, поскольку действует так называемый «эстафетный механизм» перемещения ионов гидроксония и гироксила. В цепочке, построенной из молекул воды, заряд может перейти от одного конца цепочки к другому в результате сравнительно небольшого перемещения протонов, образующих водородные связи между молекулами воды, например:
Из приведенной схемы видно, что перемещение электрического заряда происходит без перемещения атомов водорода. Иными словами, вместо одного иона Н+, двигающегося в растворе, существует эффективное движение иона Н+ , включающее образование и разрыв связей вдоль длинной цепочки молекул воды. Аналогичную схему легко изобразить и для перемещения гидроксид-иона.
Повышение температуры влияет на абсолютную скорость движения ионов путем дегидратации и уменьшения вязкости среды, что способствует увеличению скорости перемещения ионов.
Удельная электрическая проводимость
Электрическая проводимость (L) –– это способность веществ проводить электрический ток под действием электрического поля. Она представляет собой величину обратную электрическому сопротивлению R:
L = 
(2)
Единицей электрической проводимости в CИ является сименс (См), и 1 См = 1 Ом–1.
Известно, что R = r 
, поэтому L = = 
, так как 
= æ , то:
L == æ × 
, (3)
где æ (каппа) – удельная электрическая проводимость (См/м), S – площадь плоских электродов (м2), между которыми заключен раствор,ℓ – расстояние между электродами (м).
Удельной электрической проводимостью называется электрическая проводимость 1м3 раствора, находящегося в однородном электрическом поле при напряженности 1 В/м. Единицей удельной проводимости в CИ служит сименс/метр (См/м). Удельная электрическая проводимость зависит от многих факторов и, прежде всего, от природы электролита, его концентрации и температуры. Изотермы удельной электрической проводимости (рис.1) дают представление о характере зависимости удельной электрической проводимости от природы электролита и его концентрации для 250С (298К). Анализ изотермы позволяет сделать следующие выводы:
1. Удельная электрическая проводимость максимальна для растворов сильных кислот и несколько меньше – сильных оснований, что объясняется полной диссоциацией этих электролитов и высокой подвижностью ионов Н3О+ и ОН–.
2. Наименьшие значения во всем диапазоне концентраций имеет удельная электрическая проводимость растворов слабых электролитов (СН3СООН) в связи с низкой концентрацией ионов ( a
3. Удельная электрическая проводимость растет с увеличением концентрацией до некоторых максимальных значений, что отвечает увеличению количества ионов в единице объема раствора. Достигнув максимума, удельная электрическая проводимость начинает уменьшаться, несмотря на рост концентрации электролита. Подобный характер зависимости æ от С связан у сильных электролитов с уменьшением подвижности ионов из-за возрастающего по мере увеличения концентрации раствора межионного взаимодействия, а у слабых электролитов – с уменьшением степени электролитической диссоциации электролита, а значит, и уменьшением количества ионов в единице объема раствора.
С увеличением температуры удельная электрическая проводимость растет. Это обусловлено, в основном, дегидратацией ионов и уменьшением вязкости среды, т. е. уменьшением сопротивления движению ионов.
Удельная электрическая проводимость растворов зависит от разведения. Разведение величина обратная концентрации. (Разведение обозначается символом V или 1/С и характеризует объем раствора, содержащий 1 моль электролита). Когда разведение мало – раствор концентрирован и степень диссоциации слабого электролита мала. С ростом разведения a сначала увеличивается, а, следовательно, и увеличивается удельная электрическая проводимость. При дальнейшем увеличении разведения степень диссоциации приближается к единице и перестает расти, в то время как общее количество электролита в единице объема уменьшается, что вызовет падение электрической проводимости.
Удельная электрическая проводимость может быть вычислена теоретически:
æ = F × C × a × ( w А + w K ) – для слабых электролитов (4)
æ = F × C × fa × ( w А + w K ) –для сильных электролитов (5)
где F – число Фарадея, С – концентрация электролита (моль/м3), a – степень диссоциации слабого электролита, fa – коэффициент активности сильного электролита, w А и w K – абсолютная скорость движения аниона и катиона в м/сек при градиенте потенциала 1 В/м.
Молярная электрическая проводимость.
Молярная электрическая проводимость – электрическая проводимость 1 моль электролита, находящегося в растворе между параллельными электродами с расстоянием между ними 1 м и градиенте потенциала 1В/м. Между удельной электрической проводимостью и молярной электрической проводимостью (λm) существует зависимость:
где λm (лямда) – молярная электрическая проводимость, См × м2 × моль–1, æ – удельная электрическая проводимость, См × м–1; С – концентрация электролита в растворе, моль/м3.
Обычно молярная концентрация характеризуется количеством вещества в 1 дм3 (1л), а не в 1м3. В этом случае соотношение имеет вид:
Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать
Подвижность ионов и абсолютная скорость их движения связаны уравнениями
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
3.4 ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРОВ ЭЛЕКТРОЛИТОВ
3.4.1 Удельная электропроводность растворов электролитов
Электрический ток есть упорядоченное перемещение заряженных частиц. Растворы электролитов обладают ионной проводимостью (являются т.н. проводниками второго рода), т.е. электропроводность растворов электролитов обусловлена перемещением ионов в электрическом поле (в отличие от электронной проводимости проводников первого рода).
Величина преимущественного передвижения иона в направлении одного из электродов при прохождении тока через раствор отнесённая к градиенту потенциала 1 В/см, есть абсолютная скорость движения иона . Абсолютные скорости движения ионов имеют величины порядка 0,0005 – 0,003 см 2 /(В·с). Абсолютные скорости движения катионов U+ и анионов U– различаются; это приводит к тому, что ионы разных знаков переносят разные количества электричества.
Всякий проводник, по которому течет ток, представляет для него определенное сопротивление R, которое, согласно закону Ома, прямо пропорционально длине проводника l и обратно пропорционально площади сечения S; коэффициентом пропорциональности является удельное сопротивление материала ρ – сопротивление проводника, имеющего длину 1 см и сечение 1 см 2 :
, Ом (III.32)
В качестве количественной меры способности раствора электролита проводить электрический ток используют обычно удельную электропроводность κ (каппа) – величину, обратную удельному сопротивлению (т.е. величину, обратную сопротивлению столба раствора между электродами площадью 1 см 2 , находящимися на расстоянии 1 см):
, Ом -1 см -1 (III.33)
Величина удельной электропроводности электролита зависит от ряда факторов: природы электролита, температуры, концентрации раствора. Удельная электропроводность растворов электролитов (в отличие от электропроводности проводников первого рода) с увеличением температуры возрастает, что вызвано увеличением скорости движения ионов за счет понижения вязкости раствора и уменьшения сольватированности ионов. Зависимость удельной электропроводности от концентрации раствора представлена на рис. 3.9.
Рис. 3.9 Зависимость удельной электропроводности электролитов от концентрации
(1 – H2SO4, 2 – KOH, 3 – CH3COOH)
Как видно из рисунка, с увеличением концентрации удельная электропроводность растворов сначала возрастает, достигая некоторого максимального значения, затем начинает уменьшаться. Эта зависимость очень чётко выражена для сильных электролитов и значительно хуже для слабых. Наличие максимума на кривых объясняется тем, что в разбавленных растворах сильных электролитов скорость движения ионов мало зависит от концентрации, и κ сначала растет почти прямо пропорционально числу ионов; с ростом концентрации усиливается взаимодействие ионов, что уменьшает скорость их движения. Для слабых электролитов наличие максимума на кривой обусловлено тем, что с ростом концентрации уменьшается степень диссоциации, и при достижении определенной концентрации число ионов в растворе начинает увеличиваться медленнее, чем концентрация. Для учета влияния на электрическую проводимость растворов электролитов их концентрации и взаимодействия между ионами введено понятие молярной электропроводности раствора.
3.4.2 Молярная электропроводность растворов электролитов
Молярная электропроводность раствора λ есть величина, обратная сопротивлению раствора, содержащего 1 моль растворенного вещества и помещенного между электродами, расположенными на расстоянии 1 см друг от друга. С удельной электропроводностью κ и молярной концентрацией раствора С молярная электропроводность связана следующим соотношением:
, Ом -1 см 2 моль -1 (III.34)
Молярная электропроводность как сильных, так и слабых электролитов увеличивается с уменьшением концентрации (т.е. увеличением разведения раствора V = 1/С), достигая некоторого предельного значения λ o, называемого молярной электропроводностью при бесконечном разведении (рис. 3.10 – 3.11).
Рис. 3.10 Зависимость молярной Рис. 3.11 Зависимость молярной
электропроводности от концентрации. электропроводности от разведения
Для слабого электролита такая зависимость молярной электропроводности от концентрации обусловлена в основном увеличением степени диссоциации с разбавлением раствора. В случае сильного электролита с уменьшением концентрации ослабляется взаимодействие ионов между собой, что увеличивает скорость их движения и, следовательно, молярную электропроводность раствора. Последнюю связывает с абсолютными скоростями движения катионов и анионов U+ и U– уравнение Аррениуса (III.35):
(III.35)
Ф. Кольрауш показал, что в молярную электропроводность бесконечно разбавленных растворов электролитов каждый из ионов вносит свой независимый вклад, и λ o является суммой молярных электропроводностей катиона и аниона λ + и λ – (т.н. подвижностей ионов), и сформулировал закон независимости движения ионов :
Молярная электропроводность при бесконечном разведении равна сумме электролитических подвижностей катиона и аниона данного электролита.
(III.36)
Подставив в это выражение уравнение Аррениуса (III.35) и приняв, что при бесконечном разведении степень диссоциации α равна единице, получим:
(III.37)
; 
(III.38)
Электролитическая подвижность является важнейшей характеристикой иона, отражающей его участие в электропроводности раствора.
Copyright © С. И. Левченков, 1996 — 2005.
💡 Видео
Урок 19. Относительность движения. Формула сложения скоростей.Скачать
Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать
УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Ускорение. Движение с постоянным ускорением. Единица ускорения | Физика 10 класс #5 | ИнфоурокСкачать
Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать
Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать
Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать
Задачи на движение | Математика TutorOnlineСкачать
Урок 12. Равномерное прямолинейное движениеСкачать
Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать
Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать
Способы описания движения. Траектория. Путь. ПеремещениеСкачать
ФИЗИКА ЕГЭ 2024 ВАРИАНТ 3 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать
Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать
🔴 ЕГЭ-2023 по физике. Разбор варианта №20 (Демидова М.Ю., 30 вариантов, ФИПИ, 2023)Скачать
