нарушена предпосылка о гетероскедастичности остатков
все предпосылки МНК соблюдены
нарушена предпосылка о нормальном распределении остатков
Решение:
Исследования остатков ei предполагают проверку пяти предпосылок метода наименьших квадратов:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от xi;
3) гомоскедастичность остатков – дисперсия каждого отклонения ei одинакова для всех значений xi;
4) отсутствие автокорреляции остатков (значения остатков ei распределены независимо друг от друга);
5) остатки подчиняются нормальному закону распределения.
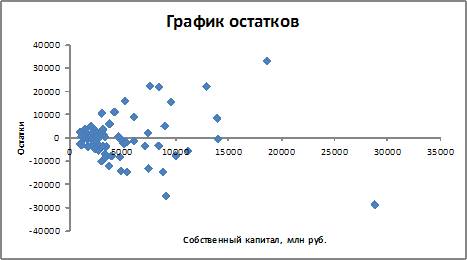
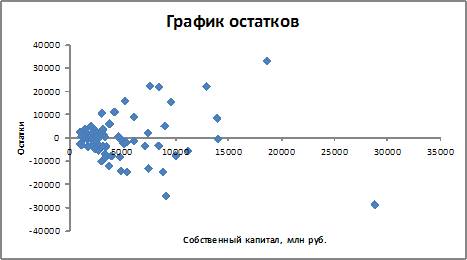
Гомоскедастичность остатков означает, что дисперсия остатков не зависит от независимой переменной. В данном случае, согласно анализу графика остатков, это не так. При небольших значениях xi величины остатков невелики, при увеличении значений xi величины остатков также увеличиваются, то есть предпосылка о гомоскедастичности остатков нарушается.
Ответы «нарушена предпосылка о гетероскедастичности остатков» и «нарушена предпосылка о наличии автокорреляции остатков» говорят от предпосылках, которых не существует.
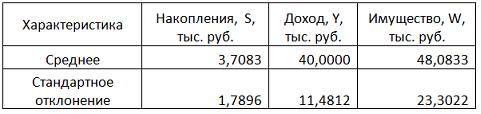
По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
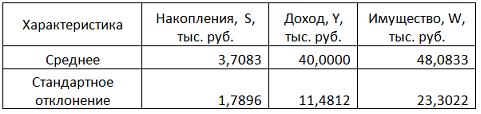
Построена матрица парных коэффициентов корреляции
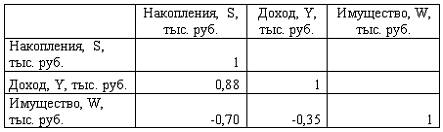
Тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии, характеризует …
Частный коэффициент корреляции
коэффициент парной корреляции между фактором и результатом
частный F-критерий Фишера
Решение:
Частный коэффициент корреляции характеризует тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Коэффициент парной корреляции между фактором и результатом характеризует тесноту связи между фактором и результатом без устранения влияния других факторов, включенных уравнение регрессии.
С помощью частного F-критерия Фишера можно проверить все коэффициенты регрессии в предположении, что соответствующий фактор был введен в уравнение регрессии последним.
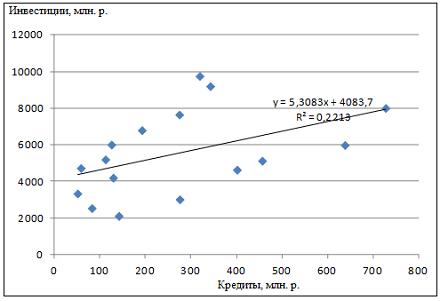
3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.

По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R 2 = 0,9708.
В уравнении, параметры которого являются значимыми, коэффициент ____________ показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения.
Регрессии
Решение:
Правильный ответ – коэффициент регрессии, он в уравнении, параметры которого являются значимыми, показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения.
Коэффициент корреляции характеризует тесноту связи между переменными.
Коэффициент детерминации – долю дисперсии, объясненной регрессией в общей дисперсии.
Коэффициент эластичности в уравнении, параметры которого являются значимыми, показывает, на сколько процентов изменится зависимая переменная у, если независимая переменная x увеличится на 1 процент.
Кейс 1 подзадача 2
1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.

Проанализировав график остатков, можно сделать вывод о том, что выполняются предпосылки метода наименьших квадратов о …
Видео:✓ Задача про делимость на 72 | ЕГЭ-2018. Задание 18. Математика. Профильный уровень | Борис ТрушинСкачать

Вопрос Пусть y
| Название | Вопрос Пусть y |
| Дата | 04.03.2018 |
| Размер | 0.76 Mb. |
| Формат файла |  |
| Имя файла | Test_RAVANDA_2.docx |
| Тип | Документы #37687 |
| страница | 7 из 8 |
| Подборка по базе: типы вопросов в английском.docx, Теоретический вопрос.docx, Экз. вопросы 2021-22, 1 курс 2 сем..docx, практическая работа. Ответить на вопросы.docx, Экзаменационные вопросы по дисциплине «Профессиональный русский , ГРАЖДАНКА вопросы.docx, Ответы на контрольные вопросы по т.docx, Комплексное рассмотрение правовых вопросов, связанных с институт, Ответы на вопросы (Ерёмин В.М. 3П Сургут).doc, 2_Барышников контрольные вопросы.doc Решение: Кейс 1, задача 3 Если для остатков модели, выполнены предпосылки МНК, то оценки параметров, полученные методом наименьших квадратов (МНК), обладают свойствами …
Решение: Кейс 1, задача 4 Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.) Решение: Кейс 2, задача 1 Функция, описывающая зависимость между порядком коэффициента автокорреляции и его значением, называется …
Решение: Кейс 2, задача 2 Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.
1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка Кейс 2, задача 3 Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.
Кейс 3, задача 1 По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
Ответ: частный коэффициент корреляции Кейс 3, задача 2 По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
стандартизированные коэффициенты регрессии Кейс 3, задача 3 По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
х1целесообразно включать в уравнения регрессии после того, как в него был включен факторх2 Кейс 3, задача 4 По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
Сначала найдем уравнение регрессии в стандартизированном виде. Будем считать х1– доход,х2– имущество. Коэффициенты парной корреляции известны и равны. Итак,
= 3,7083 — 0,11 · 40 — ( -0,03)·48,0833=0,75. Кейс 4, задача 1 В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х– объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.
Средняя ошибка аппроксимации по уравнению регрессии, построенному по всей выборке, равна ____ %. (Полученное значение округлите до целых.) Кейс 4, задача 2 В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.
Верными относительно полученного уравнения регрессии и коэффициента детерминации утверждениями, которые учитывают характер выборки, являются … высокое значение коэффициента детерминации определяется наличием в выборке аномальных значений полученное уравнение не рекомендуется использовать для прогнозирования высокое значение коэффициента детерминации говорит о том, что между объемом кредитов и объемом инвестиций в основной капитал существует тесная линейная зависимость полученное уравнение имеет высокую прогнозную силу Данные упорядочены по возрастанию объемов кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Даже беглый взгляд на данные позволяет заметить, что Московская область является аномальным значением – в ней обе переменные имеют значения, в разы превосходящие все остальные величины. Такие значения называются аномальными, или выбросами. На рисунке показано расположение точек всей выборки и уравнение регрессии, построенное по ней.
Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными не является сильной и высокой прогнозной силой уравнение не обладает. Видео:Экономическая задача №16 с нуляСкачать  По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице. х1 целесообразно включать в уравнения регрессии после того, как в него был включен фактор х2 х2 целесообразно включать в уравнения регрессии после того, как в него был включен фактор х1 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Исключив из выборки аномальное значение (Московскую область) и построив уравнение линейной зависимости, можно утверждать, что … между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал нет линейной зависимости 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков. Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.)2,9 По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице. 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Средняя ошибка аппроксимации по уравнению регрессии, построенному по всей выборке, равна ____ %. (Полученное значение округлите до целых.)36. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике. Видео:Задание 10 ЕГЭ по математике #4Скачать  По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице х1 целесообразно включать в уравнения регрессии после того, как в него был включен фактор х2 х2 целесообразно включать в уравнения регрессии после того, как в него был включен фактор х1 х1 нецелесообразно включать в уравнения регрессии после того, как в него был включен фактор х2 х2 нецелесообразно включать в уравнения регрессии после того, как в него был включен фактор х1 Решение: Частные F-критерии Итак, коэффициент детерминации равен 3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Исключив из выборки аномальное значение (Московскую область) и построив уравнение линейной зависимости, можно утверждать, что … между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал нет линейной зависимости коэффициент регрессии в полученном уравнении оказался незначимым, значит, его можно признать равным нулю при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал увеличиваются на 5,3 млн руб. при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал уменьшаются на 5,3 млн руб. Решение: Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными является слабой. Кейс 1 подзадача 4 1. По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков. Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.) Решение: Статистика Дарбина–Уотсона вычисляется по формуле 📸 ВидеоМодель Леонтьева. Теория и решение задачи.Скачать  Экономическая задача на вклады и кредиты | ЕГЭ по математике | Эйджей из ВебиумаСкачать  Геометрическая прогрессия. Задание с практическим содержанием.Скачать  Профильный ЕГЭ 2022 математика - задача 17 экономическая. Летняя школа #6Скачать  Задача 17 из профильного ЕГЭ по математике. Банки, вклады, кредиты. Антон взял кредит в банке.Скачать  Показательная зависимость 4. Функциональное уравнениеСкачать  Как спрос и предложение задают ценыСкачать  ✓ Все типы экономических задач | Задание 15. ЕГЭ. Математика. Профильный уровень | Борис ТрушинСкачать  Иррациональное уравнение в задаче 13, это законно? Профильный ЕГЭ математикаСкачать  Экономическая задача. ЕГЭ профиль.Скачать  Урок 11. Решение текстовых задач. Задачи на движение, задачи на работу. Вебинар | МатематикаСкачать  Все типы экономических задач №16 на ЕГЭ 2023 | Математика ЕГЭ — Эрик ЛегионСкачать  КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать  Урок 73 (осн). Задачи на вычисление работыСкачать  Все экономические задачи из ЕГЭ | Профильная математика ЕГЭ 2023 | УмскулСкачать  ✓ Система неравенств с параметром | ЕГЭ-2017. Задание 17. Математика. Профиль | Борис ТрушинСкачать  |

 , где
, где  – коэффициент автокорреляции первого порядка. Поскольку
– коэффициент автокорреляции первого порядка. Поскольку 
 .
.

 =
= =
= 0,7236;
0,7236; =
= =
= -0,4467.
-0,4467. .
. ;
;












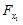 и
и  оценивают статистическую значимость присутствия факторов х1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения одного фактора после другого.
оценивают статистическую значимость присутствия факторов х1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения одного фактора после другого.  . Будем считать х1 – доход, х2 – имущество. Коэффициенты парной корреляции известны и равны
. Будем считать х1 – доход, х2 – имущество. Коэффициенты парной корреляции известны и равны 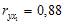 ,
, 

 =
=  =
=  0,7236;
0,7236;  =
=  =
=  -0,4467.
-0,4467.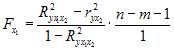 =
=  81,89> Fтабл, значит, целесообразно включить в уравнения регрессии фактор х1 после того, как в него был включен фактор х2.
81,89> Fтабл, значит, целесообразно включить в уравнения регрессии фактор х1 после того, как в него был включен фактор х2. =
=  31,21> Fтабл, значит, целесообразно включить в уравнения регрессии фактор х1 после того, как в него был включен фактор х2.
31,21> Fтабл, значит, целесообразно включить в уравнения регрессии фактор х1 после того, как в него был включен фактор х2.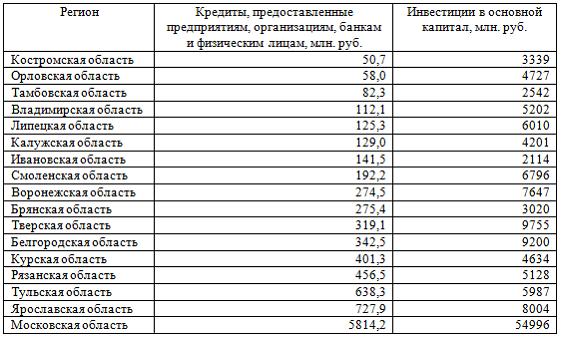

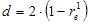 , где
, где  – коэффициент автокорреляции первого порядка. Поскольку
– коэффициент автокорреляции первого порядка. Поскольку