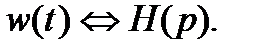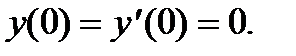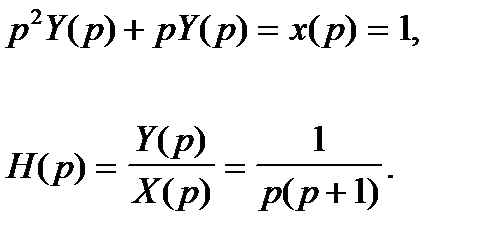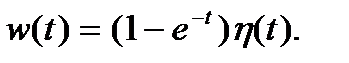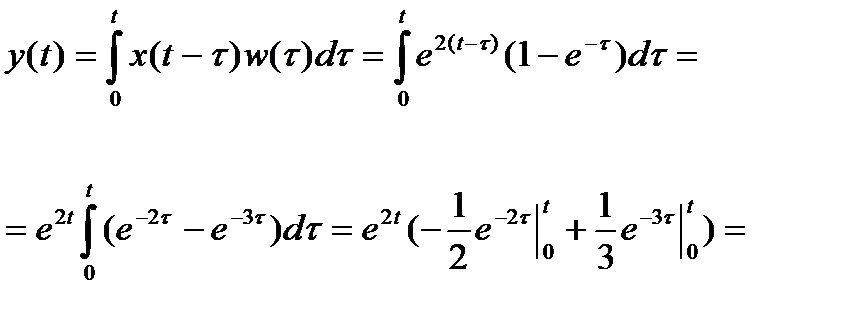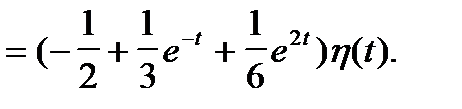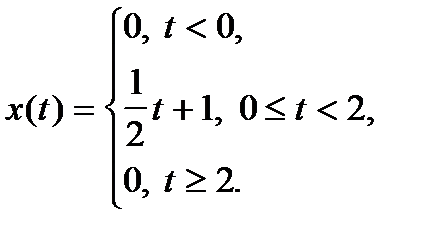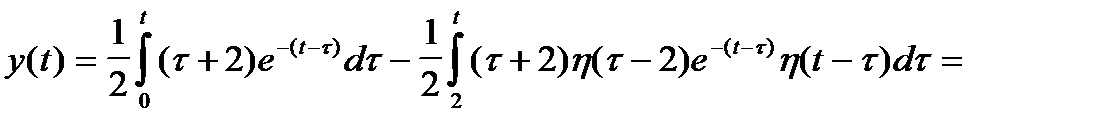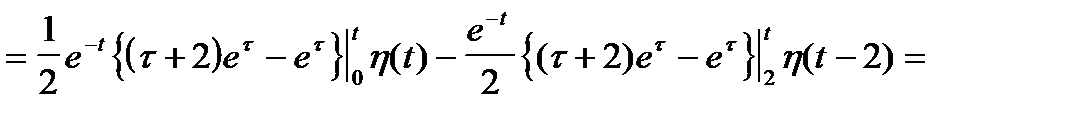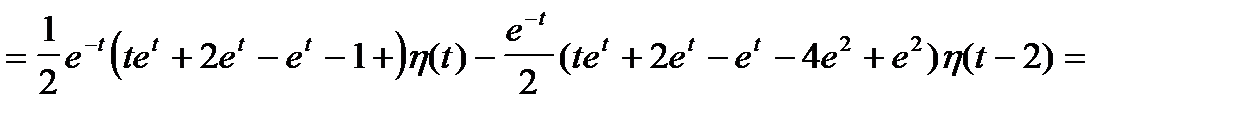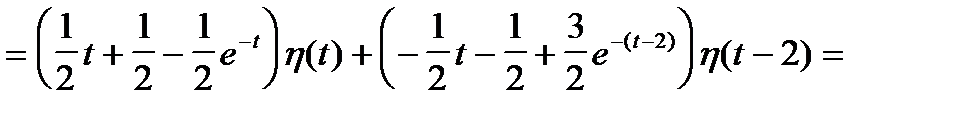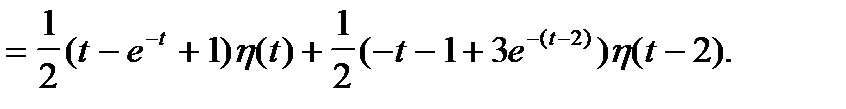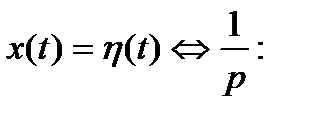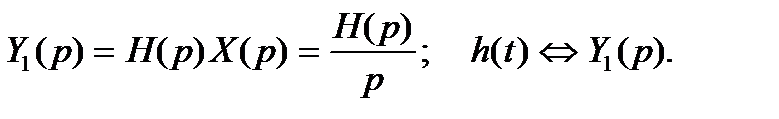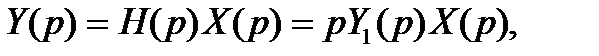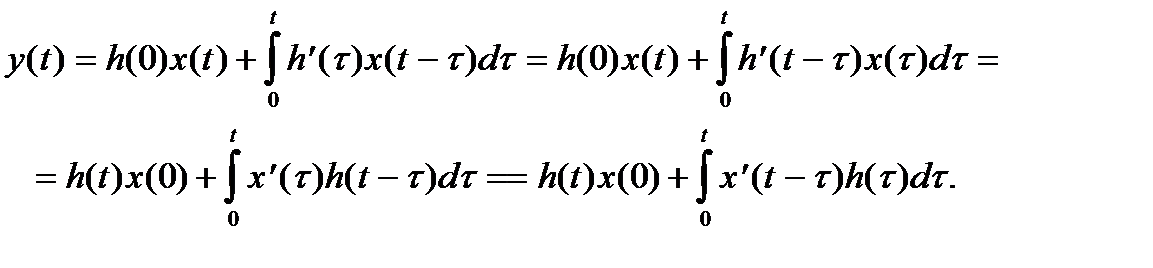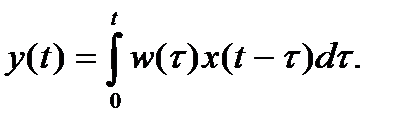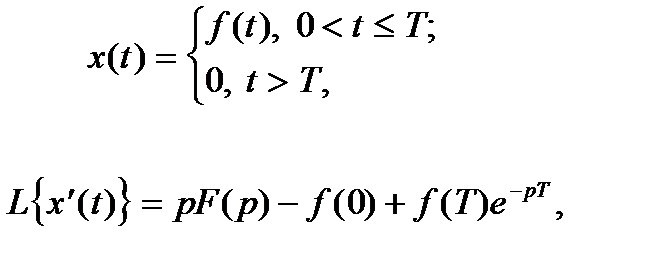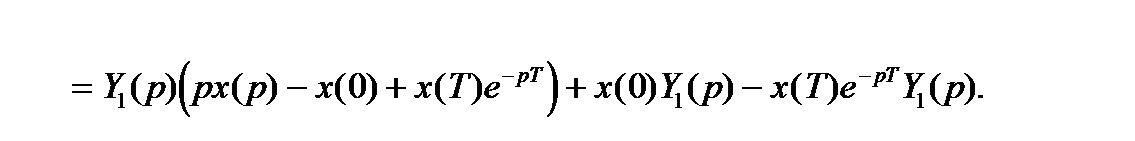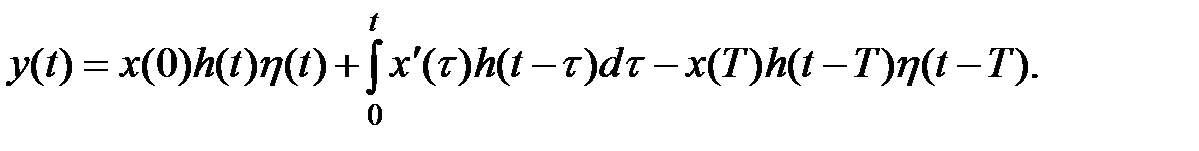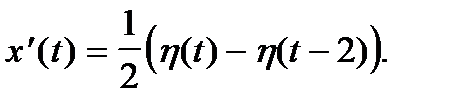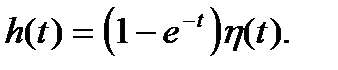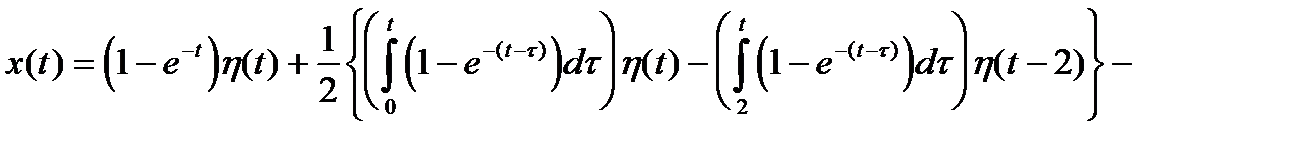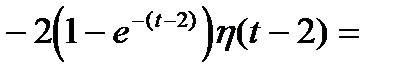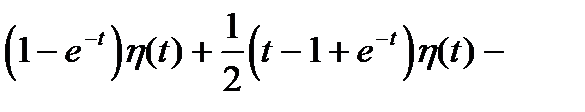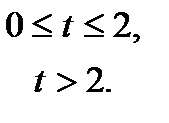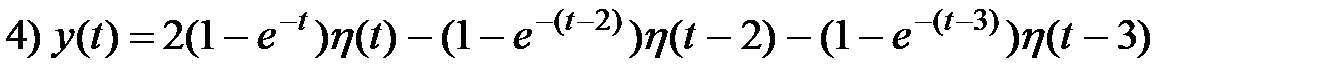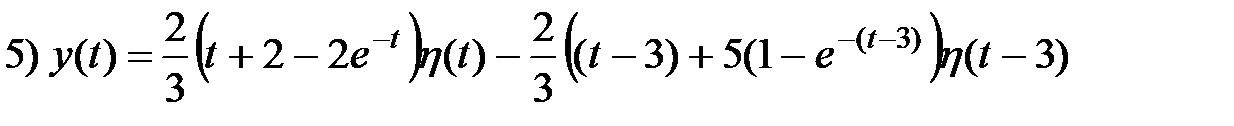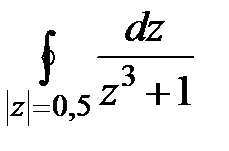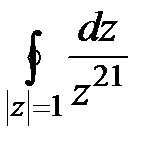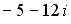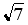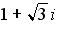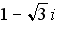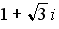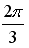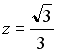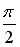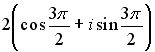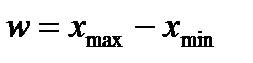Про уравнения - легко » Статьи

Решение дифференциальных уравнений методом функции грина

Обновлено
Решение линейных дифференциальных уравнений методом свертки (формула Грина, формула Дюамеля)

Рассмотрим линейное дифференциальное уравнение в операторной форме при нулевых начальных условиях:

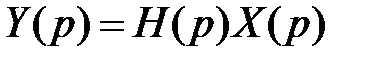
Решение дифференциальных уравнений методом функции грина.

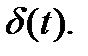
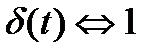
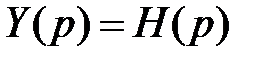
Пусть входное воздействие является импульсной функцией Решение дифференциальных уравнений методом функции гринаПоскольку Решение дифференциальных уравнений методом функции грина, изображение выходного сигнала совпадает с передаточной функцией:

Решение дифференциальных уравнений методом функции грина.

Функцией Грина (или функцией веса в теории управления) линейного дифференциального уравнения называют отклик системы на импульсное входное воздействие или оригинал передаточной функции:

Решение дифференциальных уравнений методом функции грина

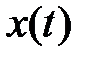
Поскольку изображение выходного сигнала Решение дифференциальных уравнений методом функции гринаявляется произведением изображений, то и оригинал Решение дифференциальных уравнений методом функции гринаможно представить как свертку оригиналов Решение дифференциальных уравнений методом функции гринаи Решение дифференциальных уравнений методом функции грина:

Решение дифференциальных уравнений методом функции грина

Таким образом, при известной функции Грина можно найти отклик системы на любое внешнее воздействие.

Пример 8. Найти частное решение дифференциального уравнения

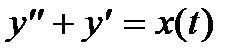
Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина

Взяв в качестве правой части импульсную функцию 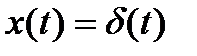Решение дифференциальных уравнений методом функции гринаи переходя к изображениям, получим передаточную функцию:

Решение дифференциальных уравнений методом функции грина:

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Возвращаясь к оригиналам, получаем функцию Грина:

Решение дифференциальных уравнений методом функции грина

Теперь, задавая любым образом правую часть x(t), можно найти решение дифференциального уравнения.

Пусть 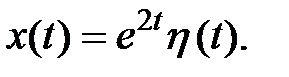Решение дифференциальных уравнений методом функции гринаТогда

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Пример 9. Найти частное решение дифференциального уравнения

Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина.

Правая часть уравнения задана функцией

0 2 2
x(t)
t

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

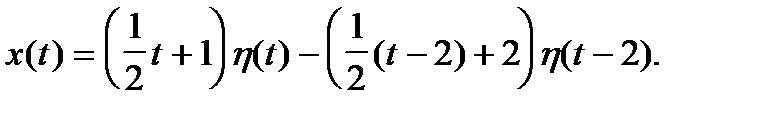
Для применения формулы свертки следует записать Решение дифференциальных уравнений методом функции грина, используя ступенчатые функции Хевисайда:

Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

С учетом того, что функция Грина для этого уравнения имеет вид Решение дифференциальных уравнений методом функции гринаполучаем решение Решение дифференциальных уравнений методом функции грина:

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Другой способ записи решений дифференциальных линейных уравнений с использованием свертки основан на формуле Дюамеля. Характеристикой системы в этом случае служитпереходная функция Решение дифференциальных уравнений методом функции грина, которая определяется как реакция (отклик) системы на постоянное воздействие

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

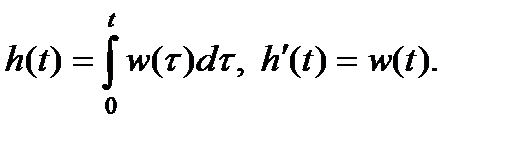
Из последнего выражения и свойства интегрирования оригинала следует, что функция Решение дифференциальных уравнений методом функции гринаи Решение дифференциальных уравнений методом функции гринасвязаны соотношениями:

Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина

С учетом того, что

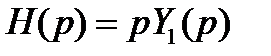
Решение дифференциальных уравнений методом функции грина,

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции гринаможно записать по формуле Дюамеля следующим образом:

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

Заметим, что при условии 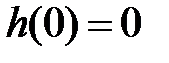Решение дифференциальных уравнений методом функции гринадве первых формы записи решения совпадают с записью

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

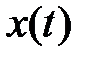
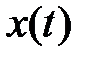
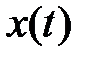
Также напомним, что в силу условий вывода формулы Дюамеля приведенные формулы можно непосредственно использовать для непрерывных функций Решение дифференциальных уравнений методом функции грина. В том случае, если функция Решение дифференциальных уравнений методом функции гринаимеют точки разрыва первого рода, следует точно записывать эту функцию, учитывая скачкообразное изменение функции в точках разрыва или другим способом учесть эти изменения. Например, если правая часть Решение дифференциальных уравнений методом функции гринаимеет вид:

Решение дифференциальных уравнений методом функции грина

то и формула Дюамеля принимает вид:

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

Переходя к оригиналам, получаем

Решение дифференциальных уравнений методом функции грина

Применим формулу Дюамеля для решения примера 9.

Пример 9 (продолжение)

x¢(t)
2 t
1/2

Производная функции, стоящей в правой части уравнения равна: Решение дифференциальных уравнений методом функции грина

Переходная функция системы имеет вид:

Решение дифференциальных уравнений методом функции грина

Видео:Метод функции ГринаСкачать

Метод функции Грина

Тогда вычисляя по формуле

Решение дифференциальных уравнений методом функции грина

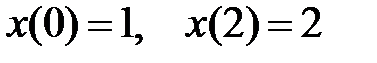
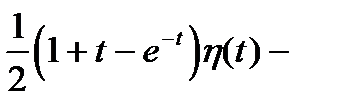
с учетом того, что Решение дифференциальных уравнений методом функции грина, получаем:

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

= Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

ЗАДАЧИ

1. Решите линейные дифференциальные уравнения с использованием свертки (формула Грина, формулы Дюамеля)

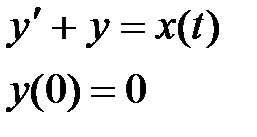
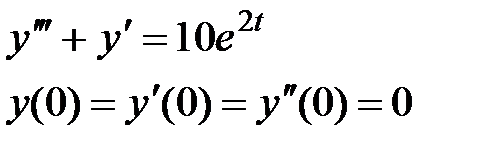
а) Решите дифференциальное уравнение Решение дифференциальных уравнений методом функции гринадля правых частей различного вида

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции гринаОтветы:

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

Решение дифференциальных уравнений методом функции грина

b) Решение дифференциальных уравнений методом функции гринаf) Решение дифференциальных уравнений методом функции грина

Контрольные вопросы:

1. Модуль и аргумент комплексного числа

2. Запись комплексного числа в показательной и тригонометрической формах

3. Степенная функция комплексного аргумента. Свойства

4. Показательная функция комплексного аргумента. Свойства

5. Логарифмическая функция комплексного аргумента. Свойства

6. Тригонометрические функции комплексного аргумента. Свойства.

7. Гиперболические функции комплексного аргумента. Свойства

8. Обратные тригонометрические функции комплексного аргумента. Свойства.

9. Обратные гиперболические функции комплексного аргумента. Свойства.

10. Понятие аналитической функции. Теорема Коши для односвязной и многосвязной областей

11. Ряд Тейлора. Область сходимости. Ряд Лорана. Область сходимости

12. Классификация изолированных особых точек.

Видео:Краевая задача.Функция Грина.Дифференциальное ур.Скачать

Краевая задача.Функция Грина.Дифференциальное ур.

13. Вычет аналитической функции в изолированной конечной особой точке. Вычет аналитической функции в бесконечно удаленной особой точке

14. Применение вычетов к вычислению контурных интегралов

15. Применение вычетов к вычислению несобственных интегралов

16. Определите характер особой точки Решение дифференциальных уравнений методом функции гринадля функций Решение дифференциальных уравнений методом функции грина

17. Вычислить Решение дифференциальных уравнений методом функции грина

18. Вычислить Решение дифференциальных уравнений методом функции грина

19. Вычислить Решение дифференциальных уравнений методом функции грина

20. Особенности ряда Фурье для четной и нечетной функции

21. Преобразование Лапласа. Функция-оригинал.

22.Обратное преобразование Лапласа. Теоремы разложения.

23. Решение линейных дифференциальных уравнений операторным методом

24. Формулы Грина и Дюамеля. Применение к решению линейных дифференциальных уравнений

25. Установите соответствие между комплексным числом и его модулем
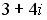
1. Решение дифференциальных уравнений методом функции грина
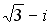
2. Решение дифференциальных уравнений методом функции грина
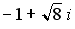
3. Решение дифференциальных уравнений методом функции грина
4. Решение дифференциальных уравнений методом функции грина

Варианты ответов:

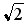
Решение дифференциальных уравнений методом функции грина5 , Решение дифференциальных уравнений методом функции грина2 , Решение дифференциальных уравнений методом функции грина3 , Решение дифференциальных уравнений методом функции грина13 , Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

26. Установите соответствие между комплексным числом и его аргументом
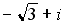
1. Решение дифференциальных уравнений методом функции грина
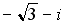
2. Решение дифференциальных уравнений методом функции грина
3. Решение дифференциальных уравнений методом функции грина

Варианты ответов:

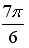
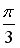
Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

27.Установите соответствие между комплексным числом и его аргументом
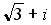
1. Решение дифференциальных уравнений методом функции грина
2. Решение дифференциальных уравнений методом функции грина
3. Решение дифференциальных уравнений методом функции грина

Варианты ответов:

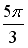
Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

28.Установите соответствие между комплексным числом и его аргументом
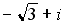
1. Решение дифференциальных уравнений методом функции грина
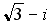
2. Решение дифференциальных уравнений методом функции грина
3. Решение дифференциальных уравнений методом функции грина

Варианты ответов:

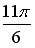
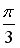
Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

29.Установите соответствие между комплексными числами 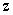Решение дифференциальных уравнений методом функции гринаи их аргументами Решение дифференциальных уравнений методом функции грина

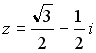
1. Решение дифференциальных уравнений методом функции грина
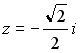
2. Решение дифференциальных уравнений методом функции грина
3. Решение дифференциальных уравнений методом функции грина

Варианты ответов:

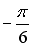
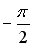
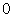
Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции гринаРешение дифференциальных уравнений методом функции грина

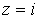
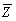
30.Произведение комплексного числа Решение дифференциальных уравнений методом функции гринана сопряженное число Решение дифференциальных уравнений методом функции гринаравно…

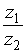
31.Частное Решение дифференциальных уравнений методом функции гринаот деления двух комплексно сопряженных чисел, где Решение дифференциальных уравнений методом функции грина, равно…

32.Дано: Решение дифференциальных уравнений методом функции грина, тогда Решение дифференциальных уравнений методом функции гринаравно …

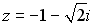
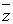
33.Произведение комплексного числа Решение дифференциальных уравнений методом функции гринаи сопряженного числа Решение дифференциальных уравнений методом функции гринаравно …

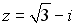
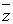
34.Произведение комплексного числа Решение дифференциальных уравнений методом функции гринаи сопряженного числа Решение дифференциальных уравнений методом функции гринаравно …

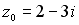
35.Значение функции Решение дифференциальных уравнений методом функции гринав точке Решение дифференциальных уравнений методом функции гринаравно…

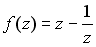
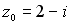
36.Значение функции Решение дифференциальных уравнений методом функции гринав точке Решение дифференциальных уравнений методом функции гринаравно…

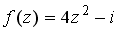
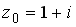
37.Значение функции Решение дифференциальных уравнений методом функции гринав точке Решение дифференциальных уравнений методом функции гринаравно…

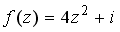
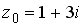
38.Значение функции Решение дифференциальных уравнений методом функции гринав точке Решение дифференциальных уравнений методом функции гринаравно…

39.Значение функции 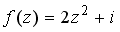Решение дифференциальных уравнений методом функции гринав точке Решение дифференциальных уравнений методом функции гринаравно…

40.Дана функция 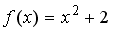Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина. Тогда коэффициент b4 разложения Решение дифференциальных уравнений методом функции гринав ряд Фурье равен…

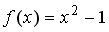
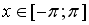
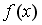
41.Дана функция Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина. Тогда коэффициент b3 разложения Решение дифференциальных уравнений методом функции гринав ряд Фурье равен…

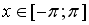
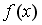
42.Дана функция Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина. Тогда коэффициент а2 разложения Решение дифференциальных уравнений методом функции гринав ряд Фурье равен…

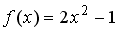
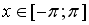
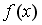
43.Дана функция Решение дифференциальных уравнений методом функции грина, Решение дифференциальных уравнений методом функции грина. Тогда коэффициент b4 разложения Решение дифференциальных уравнений методом функции гринав ряд Фурье равен…

44. Комплексное число Решение дифференциальных уравнений методом функции гринаможно представить в виде …

Варианты ответов:

Должен быть указан не менее двух вариантов ответа

1) Решение дифференциальных уравнений методом функции грина, 2) Решение дифференциальных уравнений методом функции грина, 3) Решение дифференциальных уравнений методом функции грина

РГР № 15 (0,556 ЗЕ)

Видео:Функция Грина 19122Скачать

Функция Грина 19122

Теория вероятностей и математическая статистика

Содержание работы

1.Алгебра случайных событий.

2.Случайные величины. Законы распределений. Числовые характеристики.

3.Математическая статистика. Оценки числовых характеристик. Определения закона распределения по выборке. Критерии согласия.

4.Математическая статистика: оценка коэффициента корреляции по выборочным данным, уравнение линейной регрессии.

Список литературы [2,5,12, 15, 18 ]

Номера задач указаны согласно сборнику задач по математике для втузов

, часть 3 « Теория вероятностей и математическая статистика» под ред. Ефимова А.В.М., « Наука», 1990 (№ 15 в списке литературы, имеется в библиотеке в достаточных количествах)

1. Основные понятия. Алгебра событий. № 14.1, 14.68, 14.69, 14.70,14.5, 14.7 (14.148), 14.80,4.87, 14.139, 14.191, 14.198, 14.207, 14.208-14.211, 14.214, 14.226, 14.227, 14.231, 14.233, 14.243.

2.Случайные величины. Законы распределений. Основные характеристики.

№ 14.312, 14.313, 14.323, 14.352, 14.353, 14.354, 14.278, 14.279, 14.294, 14.297, 14.300, 14.365-14.367,14.536-14.539, 14.558, 14.559, 14.560, 14,570

3.Данные для статистической обработки (задания № 3, 4) каждый студент получает от преподавателя или получает самостоятельно (утверждает у преподавателя). Подробное рассмотрение в электронном пособии (№ 18 в списке литературы)

Лабораторная работа № 1

« Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения»

1. Получите выборку из 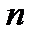Решение дифференциальных уравнений методом функции гриначисел

2. Постройте вариационный ряд (упорядочите элементы выборки по величине). При этом можно использовать соответствующую команду на панели инструментов Excel.

Видео:32. Функция ГринаСкачать

32. Функция Грина

3 .Представьте выборку в виде группированного статистического ряда (с.178- 181)

· определите размах выборки Решение дифференциальных уравнений методом функции грина

· определите число интервалов группировки одним из способов:

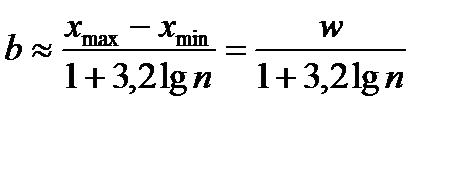
· а) Способ 1: выбираете число интервалов Решение дифференциальных уравнений методом функции грина, а затем находите шаг (ширину интервала группировки) Решение дифференциальных уравнений методом функции грина, б) Способ 2: выбираете шаг (ширину интервала группировки) по формуле Решение дифференциальных уравнений методом функции грина.

· Определите границы интервалов группировки 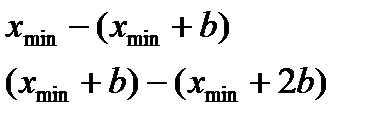Решение дифференциальных уравнений методом функции грина, и так далее до тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала)

· Найдите середину каждого интервала Решение дифференциальных уравнений методом функции грина

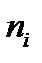
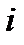
· Определите частоты Решение дифференциальных уравнений методом функции грина— число элементов выборки, содержащихся в каждом Решение дифференциальных уравнений методом функции грина-м интервале. При этом элемент, совпадающий с верхней границей интервала, условимся относить к следующему интервалу.

· Найдите накопленные частоты 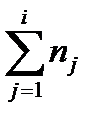Решение дифференциальных уравнений методом функции грина. При этом сумма частот по всем интервалам должна совпадать с объемом выборки Решение дифференциальных уравнений методом функции грина. Если сумма частот по всем интервалам не совпадает с объем выборки, то следует проверить, правильно ли найдены частоты.

· Найдите относительные частоты Решение дифференциальных уравнений методом функции грина, которые служат оценкой вероятности попадания элемента выборки в данный интервал

· Найдите относительные накопленные частоты Решение дифференциальных уравнений методом функции грина. Значения накопленных частот служат оценкой функции распределения и определяют эмпирическую ( выборочную) функцию распределения Решение дифференциальных уравнений методом функции грина

· Все полученные характеристики заносим в таблицу, которую называют статистическим рядом ( табл. 1.1 на стр. 181)

Номер интервалаГраницы интервалаСередина Интервала 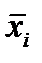Решение дифференциальных уравнений методом функции гринаЧастота 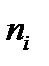Решение дифференциальных уравнений методом функции гринаНакопленная Частота 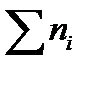Решение дифференциальных уравнений методом функции гринаОтноситель- ная частота 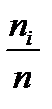Решение дифференциальных уравнений методом функции гринаНакопленная Относитель- ная частота 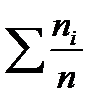Решение дифференциальных уравнений методом функции грина
·······
·······

· Представить выборку графически (стр. 182-183)

· строим полигон частот— ломаную с вершинами в точках ( 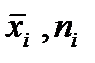Решение дифференциальных уравнений методом функции грина)

· строим полигон относительных частот— ломаную с вершинами в точках ( Решение дифференциальных уравнений методом функции грина)

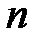
· строим гистограмму —кусочно-постоянную функцию, которая на каждом интервале группировки принимает значение Решение дифференциальных уравнений методом функции грина. Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки Решение дифференциальных уравнений методом функции грина.

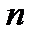
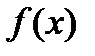
Полигон относительных частот является статистическим аналогом функции плотности вероятности. Гистограмма и полигон частот отличаются от указанной характеристики растяжением в Решение дифференциальных уравнений методом функции гринараз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности Решение дифференциальных уравнений методом функции грина.

Примечание. Все перечисленные выше операции можно провести вручную или с использованием компьютерных программ. Самое доступное математическое обеспечение – Microsoft Excel при помощи команд: Решение дифференциальных уравнений методом функции грина. При этом карманы (интервалы группировки) надо задать отдельно.


источники:

🌟 Видео

Одномерная функция ГринаСкачать

Одномерная функция Грина

16. Многомерная функция ГринаСкачать

16. Многомерная функция Грина

Колыбасова В.В. - Методы математической физики.Семинары - 15. Решение краевых задач. Функция ГринаСкачать

Колыбасова В.В. - Методы математической физики.Семинары - 15. Решение краевых задач. Функция Грина

Тихонов Н. А. - Методы математической физики - Функция ГринаСкачать

Тихонов Н. А. - Методы математической физики - Функция Грина

Функции Грина. Функция Грина для ОДУ. Семинар №37Скачать

Функции Грина. Функция Грина для ОДУ. Семинар №37

Нефёдов Н. Н. - Дифференциальные уравнения - Функция Грина и её свойстваСкачать

Нефёдов Н. Н. - Дифференциальные уравнения - Функция Грина и её свойства

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.

Формула ГринаСкачать

Формула Грина

Курс по ИДУ: Функция Грина и задача Штурма-Лиувилля | Занятие 4Скачать

Курс по ИДУ: Функция Грина и задача Штурма-Лиувилля | Занятие 4

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение системы дифференциальных уравнений методом Эйлера

Математика это не ИсламСкачать

Математика это не Ислам

Функция Грина волнового уравненияСкачать

Функция Грина волнового уравнения
Поделиться или сохранить к себе: