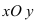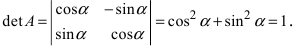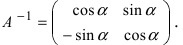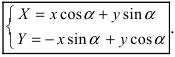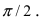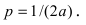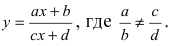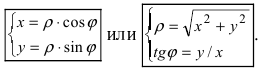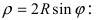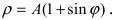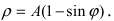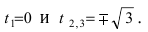Перевести уравнение кривой из полярной системы координат в декартову (5 видео)

Перевести уравнение кривой из полярной системы координат в декартову

Построим график функции в полярных координатах r=r(φ),
где 0 Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x ctg(x) Функция — Котангенс от x arcctg(x) Функция — Арккотангенс от x arcctgh(x) Функция — Гиперболический арккотангенс от x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x DiracDelta(x) Дельта-функция Дирака Heaviside(x) Функция Хевисайда Интегральные функции: Si(x) Интегральный синус от x Ci(x) Интегральный косинус от x Shi(x) Интегральный гиперболический синус от x Chi(x) Интегральный гиперболический косинус от x

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

Содержание

Преобразования декартовой системы координат с примерами решения
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
Полярные координаты. Замечательные кривые
Примеры решений: полярная система координат
Полярная система координат: решения онлайн
📺 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Построение кривой в полярной системе координатСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

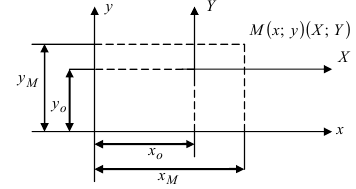
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 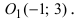Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 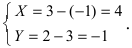Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 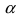(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

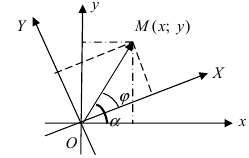
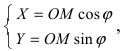
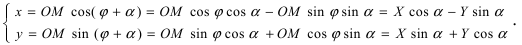
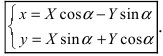
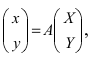
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 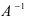обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

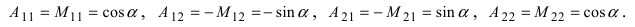
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 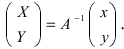Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 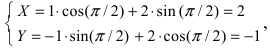т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

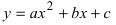
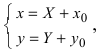
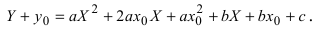
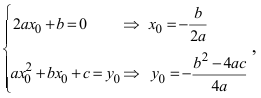
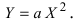
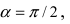
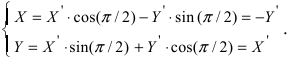
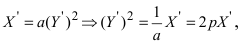
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 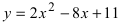к каноническому виду.

Решение:

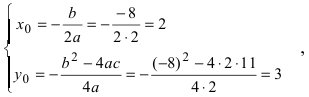
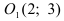
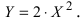
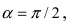
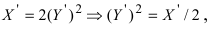
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

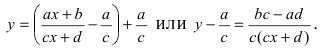
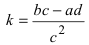
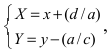
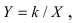
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

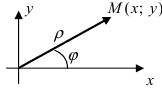
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 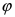между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

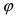
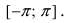
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

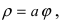
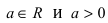
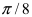
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

2. Уравнение окружности: уравнение 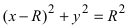описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

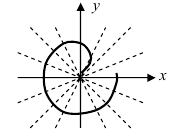
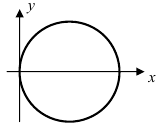
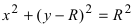
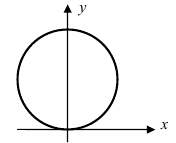
3. Уравнение описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

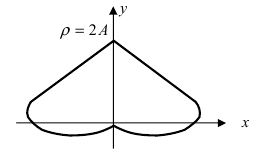
4. Кардиоиды:

Рис. 52. Кардиоида

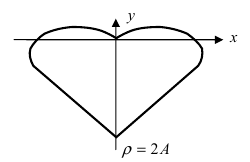
Рис. 53. Кардиоида

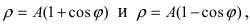
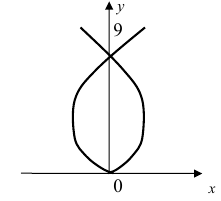
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

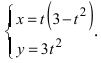
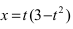
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Бесконечно малые и бесконечно большие функции
Замечательные пределы
Непрерывность функций и точки разрыва
Точки разрыва и их классификация
Экстремум функции
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Полярные в декартовыеСкачать

Примеры решений: полярная система координат

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые в полярной системе координат: табуляция функции, построение графика, переход к уравнению в декартовой системе координат т.п.

Основные этапы при работе с кривой, заданной в полярной системе координат, такие:

1. Построить полярную систему координат (изобразить полюс, полярную ось и угловые направления). Обычно строят вспомогательные лучи через $pi/6$ или $pi/8$ радиан, для большинства кривых этих точек (получается от $0$ до $2pi$ помещается 12 или 16 значений) вполне достаточно.
2. Табулируем кривую: берем последовательно все углы $phi$ (см. выше): $0$, $pi/8$, $pi/4$, $3pi/8$. и в каждой точке вычисляем значение $rho(phi)$. Заносим значения в таблицу.
3. Берем начерченную в первом пункте полярную систему координат и наносим точки. На полярной оси отмеряем значние $rho(0)$, на луче $pi/8$ — $rho(pi/8)$ и так далее.
4. Соединяем все точки плавной линией. Получается искомая кривая. Для проверки правильности можно построить дополнительно график с помощью онлайн-сервисов.
5. Если требуется найти уравнение кривой в декартовой системе координат, подставляем подходящие формулы $rho=sqrt$, $x=rhocos phi$, $y=rhosin phi$ и преобразуем.

Более подробно — в примерах ниже. Удачного изучения!

Видео:Полярная система координатСкачать

Полярная система координат: решения онлайн

Задача 1. Построить следующие кривые в полярной системе координат: Лемниската Бернулли $rho^2=2cos 2phi$ (полюс помещен в точку О).

Задача 2. Построить по точкам кривую, заданную уравнением в полярной системе координат $rho=2sin 2phi$. Найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось $Ox$ с полярной осью.

Задача 3. Дана линия своим уравнением в полярной системе координат $r=8 sin phi$. Требуется:
1) построить линию по точкам, давая $phi$ значения через $pi/6$, начиная с 0 до $2pi$.
2) Найти уравнение этой линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью.

Задача 4. Линия задана уравнением $r=18/(4+5cos phi)$ в полярной системе координат. Требуется:
Построить линию по точкам, начиная от 0 до $2pi$ и придавая $phi$ значения через промежуток $pi/8$.
Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
Назвать линию, найти координаты фокусов и эксцентриситет.