Пересчет вертикального скоростного закона в график интервальных скоростей выполняется по уравнению

Скоростная модель позволяет переводить данные из временной области в глубинную и обратно. Она является функцией F: (X,Y,TWT) → (X,Y,Z), которая каждой точке временной области ставит в соответствие точку глубинной области, при этом координаты x и y остаются неизменными. В Petrel 2016 построение скоростной модели выполняется в двух вариантах: Simple velocity model и Advanced velocity model.

В первом случае создание модели производится при наличии куба средних или интервальных скоростей. Вариант Advanced velocity model рассмотрим ниже подробнее, так как в настоящее время подавляющее большинство скоростных моделей построены именно этим способом.

Скоростная модель в Petrel представлена набором слоёв с различными скоростными характеристиками. Внутри каждого слоя по площади, скорости либо не меняются, либо меняются по одному закону. В качестве входных данных для построения скоростной модели требуются границы скоростных интервалов, представленные в виде постоянных величин, поверхностей или горизонтов структурной модели (см. рисунок ниже).

В каждом скоростном интервале необходимо задать скоростной закон и входные данные для расчета скоростей. Скоростной закон может быть нескольких видов:

1. V =V_int. Интервальная скорость, постоянная в зоне. При этом интервальная скорость может меняться по латерали. Это самый простой закон, скорости для которого можно рассчитать по минимуму входных данных (временные поверхности и скважинные отбивки в глубине). Данный закон используется либо при отсутствии достоверной скоростной информации, либо если не требуется особая детализация скоростей (например, выше целевого интервала).
2. V =V₀+kZ. Линейно изменяющаяся с глубиной мгновенная скорость. Этот скоростной закон хорошо подходит для построения скоростной модели при наличии закона время-глубина для нескольких скважин в области интереса.
3. Куб или свойство средних скоростей. Если в результате обработки сейсмических данных и расчета атрибутов были получены средние скорости, то они напрямую могут быть использованы в построении скоростной модели. Это наиболее сложный способ построения скоростной модели, позволяющий объединить несколько источников данных – скорости, полученные из обработки, скважинные скорости, а также региональные тренды. Мы не будем рассматривать этот скоростной закон в данном пособии.

Входные данные для скоростей зависят от выбранного скоростного закона. Например, при использовании закона V = V_int, интервальные скорости могут быть заданы напрямую поверхностью или константой или рассчитаны автоматически из интервальных скоростей на позициях скважин.

Скоростной закон, рассчитанный по входным данным, позволяет узнать, какая средняя скорость прохода волны соответствует каждой временной точке. Воспользовавшись этими скоростями можно пересчитать временные поверхности, заданные как границы скоростных интервалов, в глубинные.

Но мы можем иметь дополнительную информацию о положении поверхностей в глубине. Чаще всего это отбивки – выделенные по скважинным данным границы, соответствующие проинтерпретированным горизонтам. В большинстве случаев не все отбивки сидят на пересчитанных в глубину поверхностях, и скоростная модель нуждается в коррекции.

Скважинные отбивки, заданные на вход процесса Make Velocity Model, позволяют произвести коррекцию скоростной модели, отрегулировав скорости в окрестности скважин так, чтобы они в точности переводили временные поверхности в отбивки.

Готовая скоростная модель должна удовлетворять следующим критериям:

1. Заданы границы скоростных интервалов в соответствии с выделенными по скважинным данным или кубам атрибутам зонами однородности упругих свойств.
2. В каждом скоростном интервале установлен скоростной закон той детальности, которая с одной стороны достаточна для перевода локальных объектов интервала из времени в глубину без потери существенной информации, с другой – может быть обеспечена имеющимися зависимостями время-глубина (на скважинах, либо в виде кубов атрибутов).
3. Исходный скоростной закон переводит границы временных интервалов в глубину с небольшой погрешностью, которая может быть оценена по невязки полученных глубинных поверхностей и скважинных отбивок. Если невязка велика, необходимо проверить и отредактировать исходную скоростную информацию.
4. Исходный скоростной закон должен быть подвергнут коррекции – процедуре незначительного изменения скоростей для подсадки глубинных поверхностей на отбивки.

Перевод границ скоростных интервалов из временной области в глубинную с помощью скоростной модели с подсадкой скоростных границ на отбивки

Далее мы подробнее рассмотрим несколько вариантов построения скоростной модели – в зависимости от изученности области и наличия данных.

Построение скоростной модели при отсутствии скоростных данных

К сожалению, скоростные данные не всегда бывают доступны, особенно на ранней стадии работы с месторождением или при возвращении к старому проекту, данные по которому не сохранились. В такой ситуации скоростную модель можно будет построить на основе имеющейся пары время – глубина для опорных горизонтов. В качестве временной компоненты чаще всего выступает поверхность, построенная по проинтерпретированному горизонту. Глубины могут быть представлены в виде отбивок. Скоростной закон в интервале может быть рассчитан двумя способами: как константа или как поверхность, то есть скорость будет меняться по латерали. Во втором случае интервальные скорости вычисляются на позиции скважины по формуле (h2-h1)/(t2-t1) (где h2, h1 – глубины отбивок по кровле и подошве пласта в метрах, t2, t1 – одиночное время пробега волны до кровли и до подошвы в секундах), а затем экстраполируются на область интереса. При этом естественным образом происходит подсадка скоростной модели на отбивки.

Petroleum Engineers

Вы здесь

Скорости в сейсморазведке

Почитал тут пару тем и слегка обалдел. Иногда люди совсем себе не представляют, что такое скорости и с чем их кушать надо.

Поэтому небольшой ликбез на эту тему — может быть кому пригодится.

В сейсморазведке, изучающей особенности осадочного чехла для целей геологической интерпретации, существует такое понятие как скорость волны. С этим все просто: это мера того, как быстро распространяется волна в среде. Это расчетная величина — ощутить ее никоим образом не получится. Мы можем измерить только время прихода волны к приемнику, ну и глубину до слоя, породившего эту волну, когда пробурим скважину. В обшем, скорость — виртуальная величина. Злые и коварные сейсморазведчики, когда поняли это дело, решили навести туману и придумали много разновидностей этой виртуальной величины, чтобы им была работа — а другим головная боль. ))) Естественно, сделали они это исключительно в своих темных и злых целях порабощения мира.

Поэтому у нас есть цельный набор скоростей!

Ну а когда сейсмики-обработчики МОГТ подключились, то появились еще дополнительно

— Эффективные скорости (скорости ОГТ)

Из этого набора, человек (интерпретатор, модельер- называйте этого несчастного как хотите), трансформирующий поверхность из временной области в глубинную, имеет дело с ПЛАСТОВОЙ и СРЕДНЕЙ скоростями.

Ну а теперь по порядку. Начнем издалека.

Все мы знаем, что с глубиной свойства породы изменяются. Чем ниже мы опускаемся, тем, что называется, толще толща пород и тем ближе мы к горячей мантии. В этих условиях с глубиной увелчивается средняя плотность породы. А как известно из физики, в плотных телах, волны распространяются быстрее. То есть, градиенты давления и температуры обеспечивают градиент плотности и, как следствие, градиент скорости распространения сейсмических волн. Чем глубже — тем быстрее скорость.

Теперь о самих скоростях. Самый достоверный источник — это годограф ВСП или по буржуйской терминологии Checkshot. Из него мы получаем скорости наиболее близкие к реальным, к истинным.

-Истинная скорость — это мгновенная скорость распространения сейсмической волны, определяемая для каждой точки среды, через которую проходит фронт волны. Короче говоря, абстрактная математическая величина. Возможно в далеком-далеком будущем, в эпоху Звездных войн, кто-то и научится это дело мерять.

— Интервальная скорость — это скорость, измеренная для какого-то постоянного интервала. Обычно, это интервал между стоянками приемника/пунктами приема в скважине при работах ВСП, ну или шаг между измерениями для АК. Соотвественно, при измерениях скорости через ВСП интервал будет примерно равным 10 метрам, при исследованиях АК (дай бог памяти!) около 20 см. Вот в этих, примерно постоянных по толщине интервалах, мы и будем знать с какой скоростью распространялась волна!

Vинт=dX/dT, где dX — расстояние от начала до конца интервала, а dT — время прохождения этого интервала.

— Пластовая скорость. Здесь все просто. Геологи, поколдовав над большим объемом данных, приходят к мнению, что вся толща пород разбита на пласты, которые классифицируются по литологическим характеристикам. То что пишут в лито-стратиграфической колонке. Ну там, знаете. «Пласт песчанника, такой-то зернистости и окраса мощностью Х метров, пласт глин битуминозных (или не очень) мощностью У метров. » и т.д. Так вот, пластовая скорость — это скорость для какого-то конкретного пласта. По сути — это интервальная скорость, только интервалы определяются по границам геологических пластов или стратиграфическим границам.

Vпл=[H(i+1)-H(i)]/[T(i+1)-T(i)], где H(i+1) — глубина подошвы, H(i) — глубина кровли, T(i+1) — время на подошве, T(i) — время на кровле

— Средняя скорость. Это скорость от поверхности до какой-то точки в среде. Грубо говоря, это аппроксимация всего набора вышележащих слоев одним-единственным. Формульно

Vср=[X(i)-X(0)]/[T(i)-T(0)], где X(i) — глубина до точки, в которой меряем, X(0) — 0 метров, T(i) — время на точке в которой меряем, T(0) — время на 0 метров.

Или по другому: Vср=X(i)/T(i)

Отсюда следует очень важный вывод! Градиент средней скорости больше либо равен нулю (функция средней скорости монотонно возрастает). Если кто-то вам говорит про отрицательный градиент средней скорости — он или из другого измерения или кто-то кого-то накалывает. Физически отрицательный градиент возможен, когда у вас есть зона АВПД очень большой мощности и невероятно огромного давления, такого, что зерна породы практически плавают во флюиде. Средняя скорость, как следует из названия — осредняет, и чем глубже — тем сильнее нивелируются все особенности разреза. То есть на небольших глубинах градиент может быть с минусом из-за неравномерной уплотненности пород, но на глубинах 2000 и глубже, разница в скоростях должна быть просто чумачечей!

Средние и пластовые скорости используются для построения скоростных моделей, с помощью которых осуществляется преобразование время-глубина. Пластовые более предпочтительны, поскольку они более детально описывают вышележащую толщу. Средние скорости хорошо использовать в местах, где слои залегают без резких нарушений, последовательно друг на друге, где не было мощных тектонических процессов. В общем, бОльшая часть Западной Сибири.

Теперь про скорости введеные обработчиками.

— эффективная скорость. Это такая скорость, которая спрямит годограф сейсмограммы ОГТ в линию. В буржуйской терминологии normal moveout velocity. Применять ее для преобразования время-глубина, мягко говоря, не стоит. Эта скорость испытывает влияние огромного числа факторов как технического так и геологического характера. И кроме всего прочего, она расчитывается от нулевого времени сейсмической записи, о выборе которого можно писать еще одну отдельную тему.

— RMS скорость. Она определяется по формуле Урупова-Дикса. Капиталисты почему-то называют ее просто формулой Дикса, как всегда стараясь умолчать о достижениях советской науки, ну да бог им судья! RMS скорость — это аналог средней скорости, но только во временной области. По идее она гораздо правильнее описывает среду, чем эффективная скорость, поскольку в ней осреднение проводится по пластам.

— Миграционные скорости. Это скорости, которые используются для построения скоростных моделей при процедурах миграции. В зависимости от типа миграционного преобразования, эти скорости различаются. При временной миграции — это, скорее всего, средние или эффективные скорости, а при глубинной — это интервальные скорости. И вот тут необходимо раскрыть страшную тайну: средние и интревальные скорости миграции могут не иметь ничего общего с реальными средними и интервальными скоростями. После того, как структурно- скоростные модели построены, они дают информацию о том КАК и НА СКОЛЬКО изменяются скорости в межскважинной среде, но не сами эти скорости! Полученные по этим скоростным моделям структурные поверхности, нельзя рассматривать как итоговые.

Надеюсь, после прочтения, вам стала немного понятнее иерархия и классификация скоростей.

Скоростной анализ с использованием спектров скоростей

Доступные действия

Найти все файлы пользователя

Прокомментировать файл

Кафедра общей и прикладной геофизики

по распространению сейсмических волн

Скоростной анализ с использованием спектров скоростей

Выполнил: студент группы 4151

II. Теоретическая часть. 5

1. Скоростной анализ. 5

2. Спектр скоростей.. 9

III. Практическая часть. 16

1. Задаваемые для Interactive Velocity Analysis параметры 16

2. Суммирование с ослаблением кратных волн.. 20

3. Суммирование с усилением кратных волн.. 21

4. Суммирование с заданными интервалами скоростей.. 22

IV. Заключение. 24

V. Список литературы.. 25

Сейсморазведка является одним из важнейших видов геофизической разведки земных недр. Она включает в себя комплекс методов исследований геологического строения земной коры, основанных на изучении особенностей распространения в ней искусственно возбуждённых упругих волн. Вызванные взрывом или другим способом упругие волны, распространяясь во всех направлениях от источника колебания, проникают в толщу земной коры на большие глубины. В процессе распространения в земной коре упругие волны претерпевают процессы отражения и преломления. Это приводит к тому, что часть сейсмической энергии возвращается к поверхности Земли, где вызывает дополнительные сравнительно слабые колебания. Эти колебания регистрируются специальной аппаратурой. Полученные записи подвергаются глубокой обработке.

Метод отражённых волн (МОВ) – наиболее эффективный и развитый метод сейсморазведки, применяемый в наибольших объёмах при поисках и детальной разведке месторождений нефти, газа и ряда других полезных ископаемых на суше и на море. В настоящее время МОВ используется: для определения глубины и формы залегания границ раздела геологических напластований; выявления структурных и неструктурных ловушек полезных ископаемых, особенно нефти и природного газа; при благоприятных обстоятельствах для получения данных о литологии, фациальном составе пород, условии их образования, характере флюидов, насыщающих поровое пространство горных пород и др. Полевые наблюдения выполняют по специальным системам наблюдений. В настоящее время основными являются системы многократных перекрытий, обеспечивающие получение значительной избыточной информации. В настоящее время в сейсморазведке МОВ применяют преимущественно 48-кратные перекрытия с расстоянием между каналами от 25 до 100 м. После регистрации упругих волн изучают их кинематические (времена прихода, скорости распространения и др.) и динамические (амплитуда, частоты и др.) характеристики. В процессе дальнейшей обработки используют такие преобразования полевых записей, которые существенно улучшают соотношение сигналпомеха.

Основным современным вариантом реализации МОВ является метод общей глубинной точки (МОГТ). Его основ ой являются: сложные системы многократных перекрытий, сортировка исходных трасс в сейсмограммы ОГТ по принципу принадлежности их к общей средней точке (середина расстояния «источник-приёмник»), расчёт и ввод статических и кинематических поправок, последующее суммирование трасс сейсмограмм ОГТ в одну суммотрассу для каждой общей средней точки.

Принципиальные достоинства МОГТ заключаются в том, что в процессе получения временных разрезов существенно ослаблены как регулярные (кратные и обменные), так и нерегулярные волны-помехи.

Нахождение спектра скоростей является важным элементом скоростного анализа на этапе ввода и коррекции кинематических поправок. Именно спектр скоростей позволяет нужным образом выбирать скорости суммирования и получать временные разрезы в зависимости от целей – с ослаблением или усилением тех или иных волн. Кроме того, выбор скоростей является важным этапом и для перехода от временного разреза к глубинному.

В данной курсовой работе рассматривается реализация спектра скоростей для нахождения кинематических поправок и получения временного разреза.

1. Скоростной анализ

Нормальное приращение – основа для определения скоростей по сейсмическим данным. Рассчитанные скорости могут быть использованы для поправки за нормальное приращение, чтобы выровнять отражения в трассах выборки ОСТ перед суммированием. Скорость суммирования – скорость, при использовании которой для коррекции кинематических поправок получают оптимальный суммарный разрез. Данное определение в значительной мере субъективно, не говоря уже о том, что на самом деле скорость суммирования выбирается по результатам анализа скоростей суммирования.

Скоростной анализ (t 2 – x 2 )

По уравнению (1) мы можем разработать практический способ определения скорости суммирования, используя выборку ОСТ:

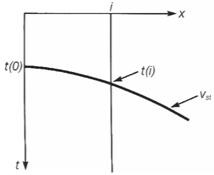
где v_st – скорость, обеспечивающая наилучшую аппроксимацию гиперболой кривой времени пробега t_st(x) на выборке ОСТ в пределах длины расстановки.

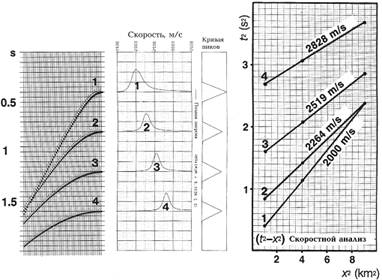
Это уравнение описывает линию на поверхности (t 2 , x 2 ). Наклон линии равен 1/v 2 _st, а величина, при которой происходит пересечение х = 0, равна t(0). Синтетическая выборка на рис.2 была выведена из скоростной модели на рис.1. На правом изображении рис.2 показаны выбранные времена пробега четырех сигналов при различных выносах в плоскости (t 2 , x 2 ). Чтобы найти скорость суммирования для данного сигнала, точки, соответствующие этому сигналу, соединены прямой линией. Обратная величина наклона (углового коэффициента) – квадрат скорости суммирования. На практике для определения угловых коэффициентов можно использовать аппроксимацию методом наименьших квадратов.

Рис.1 Гипотетическая скоростная функция, использованная при формировании синтетической выборки ОСТ.

Рис.2 Скоростной анализ (t 2 – x 2 ), примененный к синтетической выборке, которая получена по скоростной функции, показанной на рис.1.

Центральное изображение – скоростной спектр, основанный на уравнении (5).

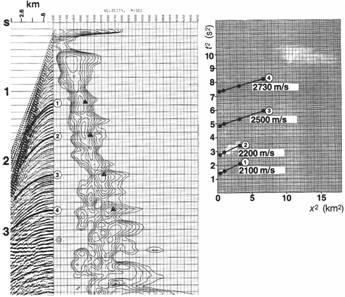
Скоростной анализ (t 2 – x 2 ) – это надежный способ оценки скоростей суммирования. Точность метода зависит от отношения сигнал помеха, которое влияет на количество пикинга. На рис.2 сопоставляются результаты применения спектра скоростей (центральное изображение). Пример реальных данных показан на рис.3. Скорости, оцененные по анализу (t 2 – x 2 ), обозначены на спектре треугольниками. Соответствие между подходом (t 2 – x 2 ) и выбором по спектру скоростей вполне удовлетворительное.

Рис.3 Скоростной анализ (t2 –x2), примененный к выборке ОСТ.

Треугольники на скоростном спектре (среднее изображение) получены на основании уравнения (5) и представляют скорости, полученные по угловым коэффициентам линий, показанных на графике справа.

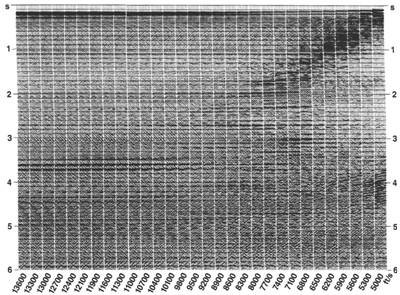
Получить достоверную скоростную функцию необходимо для того, чтобы добиться суммы сигнала лучшего качества. Следовательно, скорости суммирования часто оцениваются по данным, суммированным по нескольким постоянным скоростям на основе амплитуды и выдержанности суммированного сигнала. Этот подход показан на рис.4.

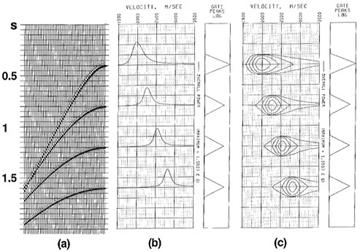
Здесь часть профиля, содержащая 24 выборки ОСТ (обычно количество выборок может изменяться от 24 до 48, но сюда может входить и весь профиль) исправлена за нормальное приращение и суммирована с несколькими постоянными скоростями. Полученные в результате 24-трассные суммы ОСТ были отображены в виде панели, где скорости суммирования возрастают справа налево.

Рис.4 Суммы при постоянных скоростях 24 выборок ОСТ (5000 – 13000 фт/с).

Скорости суммирования пикированы непосредственно с панели суммы постоянной скорости (CVS) путем выбора скорости, которая дает наилучший суммарный отклик на выбранном времени. Обратите внимание на когерентные помехи, присутствующие в данных. Сигнал на времени 3.6с суммируется в широком диапазоне скоростей. Это свидетельствует о снижении разрешающей способности оценок скоростей для сигналов, соответствующих большим глубинам. Причина этой проблемы заключается в том, что в общем случае нормальное приращение увеличивается с глубиной.

Следует быть осторожнее при выборе постоянных скоростей, используемых в вышеописанном методе CVS. Кроме того, что в разрезе скорости изменяются в широких пределах, следует учитывать два обстоятельства: 1) диапазон скоростей, необходимых для суммирования данных и 2) шаг между пробными скоростями суммирования. При выборе диапазона скоростей нужно обратить особое внимание на тот факт, что сигналы от наклонных отражающих поверхностей и полезные сигналы, смещенные от плоскости наблюдения, могут иметь аномально высокие скорости суммирования. При выборе шага между постоянными скоростями следует помнить, что основой для оценки скорости является приращение, а не скорость. Следовательно, предпочтительнее делать развертки приращений равных Dt_NMO, нежели равных v_NMO. Это предотвращает избыточное квантование высокоскоростных сигналов и недостаточное квантование низкоскоростных сигналов. Хороший способ выбора D(Dt_NMO) – чтобы разность приращения между соседними пробными скоростями при максимальном суммарном выносе составляла приблизительно 1/3 видимого периода данных. Неглубокие данные характеризуются короткими максимальными выносами из-за обнуления, а глубинные данные имеют большой видимый период. Следовательно, можно уменьшить количество пробных скоростей суммирования.

Метод CVS особенно полезен на участках со сложным строением, позволяя интерпретатору непосредственно выбирать сумму с лучшей выдержанностью сигнала (часто скорости суммирования сами по себе имеют минимальное значение). Суммы постоянных скоростей часто содержат много трасс ОСТ и иногда состоят из всего профиля.

Метод спектра скоростей рассмотрен в следующем разделе. В отличие от метода CVS, он основан на взаимной корреляции трасс в выборке ОСТ, а не на выдержанности суммированных сигналов в латеральном направлении. Поэтому данный метод больше подходит для данных, где имеется проблема кратных отражений и является менее подходящим для случая сложного строения.

2. Спектр скоростей

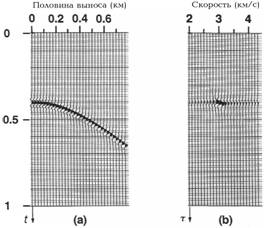
Входная выборка на рис.5а содержит один годограф отражения от плоской границы. Средняя скорость над ОП равна 3000м/с. Предположим, что эта выборка несколько раз исправлена за нормальное приращение и суммирована с применением нескольких постоянных скоростей от 2000 до 4300м/с. На рис.5b показаны результирующие суммарные трассы для каждой скорости на плоскости «скорость – полное вертикальное время». Это изображение называется спектром скоростей. Мы преобразовали данные из области «вынос – полное время пробега» (рис.5а) в области «скорость суммирования – полное вертикальное время» (рис.5b).

Рис.5 Спектр скоростей.

Максимальная суммированная амплитуда имеет место при скорости 3000м/с. Это скорость, которая должна быть использована для суммирования сигнала во входной выборке ОСТ. Низкоамплитудная горизонтальная полоска на спектре скоростей обусловлена вкладом со стороны малых удалений, тогда как высокоамплитудная область вызвана вкладом со стороны всего множества выносов. Следовательно, дальние выносы необходимы на спектре скоростей для улучшения разрешающей способности.

Каждая трасса в выборке [v, t = t(0)] (b) – это сумма трасс в выборке ОСТ (а), где используются поправки за нормальное приращение при постоянной скорости.

Рис.6 Определение положения оси выносов на оси скорости.

Выборка ОСТ, ассоциированная со слоистой моделью, показана на рис.6а. Исходя из спектра скоростей, выбраны следующие значения для функции скоростей суммирования (рис.5b): 2700, 2800, 3000м/с. Эти величины соответствуют неглубоким, средним по глубине и глубинным отражениям. Спектр скоростей может не только представить функцию скоростей суммирования, но и позволяет различать первичные и кратные отражения.

Величина, изображенная на спектрах скоростей на рис.5b и 6b – это суммарная амплитуда. При малом отношении сигнал/помеха суммарная амплитуда может не иметь достаточную величину. Цель скоростного анализа состоит в получении точек, которые соответствуют лучшей когерентности сигнала вдоль гиперболической траектории по всей длине расстановки выборки ОСТ. Neidell и Taner (1971) обобщили различные типы мер когерентности, которые могут быть использованы в качестве признаков при расчете спектров скоростей.

Рассмотрим выборку ОСТ с одним отражением (рис.7). Суммарная амплитуда определяется как:

(2)

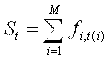
где f_i,t(i) – величина амплитуды на i-трассе при полном времени пробега t(i). Здесь М – количество трасс в выборке ОСТ. Полное время пробега t(i) располагается вдоль пробной гиперболы суммирования:

Нормализованная суммарная амплитуда определяется как

(4)

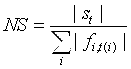
Рис.7 Суммарная амплитуда.

Амплитуды f_i,t(i) по гиперболе, обеспечивающей наилучшее совпадение [ур. (3)], определенной оптимальной скоростью суммирования, складываются с целью получения суммарной амплитуды s_t [ур. (2)].

NS изменяется в пределах от 0 до 1. Уравнение (4) подразумевает, что когерентность, как определено здесь, — это нормализованная суммарная амплитуда.

Другая величина, используемая в расчетах спектров скоростей – это сумма ненормированной взаимной корреляции во временном окне, которое следует гиперболе пробега суммирования по выборке ОСТ. Выражение для суммы ненормированной взаимной корреляции имеет вид:

(5)

где СС можно интерпретировать как полуразность выходной энергии суммы и входной энергии. Нормированная форма СС – это другой признак, который часто используется в расчетах скоростных спектров и имеет вид:

(6)

Сумма взаимной корреляции, нормированная по энергии, определяется как:

(7)

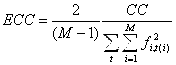
ЕСС изменяется в пределе – [1/(M-1)] 2 (t)

Нормальная сумма взаимной корреляции, NCC11Сумма взаимной корреляции, нормированной по энергии, ECC0.8-0.8Подобие, NE0.90.1

По результатам, приведенным в таблице 1, можно сделать несколько заключений. Суммарная амплитуда чувствительна к полярности трассы. Ненормированная взаимная корреляция обеспечивает лучшее выделение интенсивных отражений на спектре скоростей, тогда как нормированная или нормированная по энергии взаимная коррекция позволяет выделить на спектре скоростей слабые отражения. Как следует из уравнения (9), подобие – это не более чем смещенная версия суммы взаимной корреляции, нормированной по энергии.

Обычно спектр скоростей не отображается так, как показано на рис.5b. Два наиболее распространенных типа изображения используются для выбора скоростей в форме ряда окон или изолиний (рис.8), причем последней форме обычно отдается предпочтение. Другая величина, помогающая сделать выбор, — это наибольшая из величин когерентности из каждого временного окна, отображенных в функции времени справа от спектра скоростей на рис.8. Если не указано иначе, ненормированная корреляция использовалась для построения спектра скоростей синтетической выборки ОСТ, которая используется в последующих обсуждениях.

Рис.8 Два способа отображения спектра скоростей, выведенного по выборке ОСТ (a), (b) ряд окон, (с) в виде изолиний.

Расчёт практической части проведён в обрабатывающей системе RadEx Pro. Пакет предназначен для обработки многоканальных сейсмоакустических данных на компьютерах, работающих под управлением операционной системы MS Windows. По структуре и интерфейсу пакет близок к наиболее распространенным пакетам обработки, таким как Promax, Geovectur, IXL, Omega.

1. Задаваемые для Interactive Velocity Analysis параметры

Модуль Interactive Velocity Analysis используется для интерактивного анализа скоростей и контроля качества вводимых скоростей. Во входных данных должны быть корректно заполнены следующие поля заголовков:

· SCDP — номер суперсейсмограммы ОГТ. Если ввод данных в поток происходит при помощи модуля Super Gather, то это поле присваивается автоматически. В противном случае его следует присвоить вручную.

· OFFSET и AOFFSET — должны содержать выносы и их абсолютные значения соответственно.

· ILINE_NO и XLINE_X — в случае 2D данных, в первое поле следует записать номера точек ОГТ (CDP), а во второе поле — любое одинаковое целое значение.

Интерфейс модуля состоит из двух частей: окно установки начальных параметров и основное рабочее окно модулем во время его выполнения. Диалоговое окно установки параметров может быть вызвано также и при работе модуля, но при этом все изменения параметров будут активны лишь во время текущего сеанса выполнения модуля.

При активации модуля появляется окно задания параметров модуля, содержащее 9 вкладок:

· Super Gather. На этой вкладке доступна только опция Bin offsets, аналогичная одноименной опции из окна параметров модуля Super Gather.

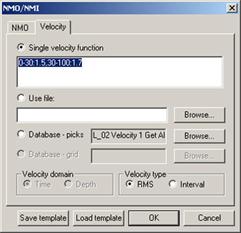
· Input velocity. Здесь необходимо ввести скоростной закон, который будет применен к данным на входе. Вкладка аналогична окну, появляющемуся при активации модуля NMO/NMI.

· Output velocity. Необходимо задать текстовый файл, который будет содержать отредактированное поле скоростей. Вкладка аналогична окну, появляющемуся при активации модуля NMO/NMI, за исключением опции Single velocity function, которая отсутствует на вкладке.

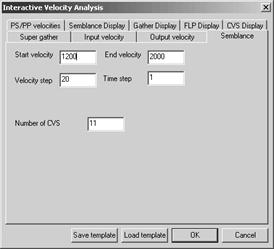
· Semblance. Вкладка задает параметры расчета коэффициентов подобия и имеет следующий вид:

Рис.9. Interactive Velocity Analysis закладка Semblance.

В полях Start velocity и End velocity задаются начальная и конечная скорости для перебора скоростей. Для расчета коэффициентов подобия, шаг дискретизации по скорости задается в поле Velocity step, шаг дискретизации по времени задается в поле Time Step. Количество выводимых на экран сумм с постоянными скоростями задается в поле Number of CVS.

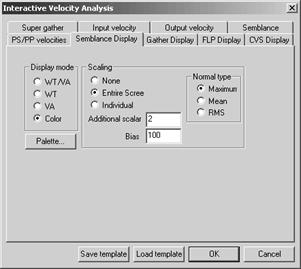
· Semblance Display Вкладка используется для задания параметров отображения спектра скоростей, рассчитанного по коэффициентам подобия (КП) и имеет следующий вид:

Рис. 10. Interactive Velocity Analysis закладка Semblance display.

· В поле Display Mode выбирается способ изображения трасс спектра скоростей:

WT/VA отображает трассы способом отклонений одновременно со способом переменной ширины записи. WT отображает трассы способом отклонений. VA отображает трассы способом переменной ширины записи. Gray отображает трассы способом переменной плотности в серой палитре. Нажав кнопку Palette… можно задать палитру вручную.

· В поле Scaling задается нормировка амплитуд трасс:

None – нет дополнительной нормировки трасс. Entire screen – нормирует все трассы в совокупности путем деления амплитуд трассы на среднее абсолютное значения амплитуды всех трасс. Individual – нормирует все трассы индивидуально путем деления амплитуд трассы на среднее абсолютное значения амплитуды самой трассы.

· Normal type. В этом поле устанавливается тип нормировка амплитуд:

· Maximum – по максимальному значению. Mean – по среднему значению. RMS – по среднеквадратичному значению.

· Additional scalar. В этом поле вводится дополнительный коэффициент, на который будут умножены значения отсчетов трасс перед выводом на экран.

· Bias. В этом поле вводится смещение среднего уровня трассы от нуля, приводящее к изменению уровня черного цвета в случае изображения способом переменной ширины записи. Положительное значение произведет сдвиг влево от нулевой линии трассы с увеличением зачерненной площади кривой. Отрицательное значение соответствует уменьшению зачерненной площади кривой.

· Gather Display. Вкладка используется для настройки параметров просмотра сейсмограммы. Вкладка имеет такой же вид, как и вкладка Semblance Display.

· FLP Display (окно суммы сформированной с текущей скоростной функцией, отпикированной в окне Semblance display). Вкладка используется для установки параметров отображения суммотрасс, полученных с использованием текущей скоростной функции, отпикированной в Semblance display. Вкладка имеет такой же вид, как и вкладка Semblance Display.

· CVS Display (окно сумм с постоянными скоростями) Вкладка используется для установки параметров отображения суммотрасс с постоянными скоростями. Вкладка имеет такой же вид, как и вкладка Semblance Display.

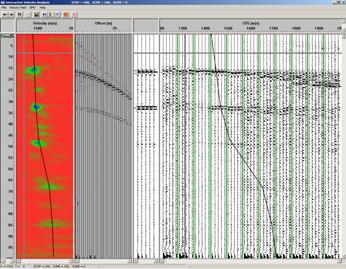
При запуске потока, содержащего модуль Interactive Velocity Analysis, открывается окно, подобное показанному на рисунке 11.

Окно разделено на 5 частей:

· Вертикальная шкала времени двойного пробега (в мс);

· Velocity — окно спектра скоростей, полученного при помощи расчета коэффициентов подобия (настройка параметров этого окна происходит на вкладке Semblance display);

Рис. 11. Interactive Velocity Analysis.

· Offset — окно просмотра сейсмограммы (настройка параметров окна происходит на вкладке Gather display);

· Окно суммотрасс, полученных с использованием текущей скоростной функции, отпикированной на спектре скоростей (настройка параметров окна происходит на вкладке FLP display);

· CVS — окно сумм с постоянными скоростями (настройка параметров окна происходит на вкладке CVS display).

В окне Interactive Velocity Analysis производится пикирование значений скорости (чёрная линия на рисунке) для достижения различных результатов суммирования. При визуальном анализе полученной картины на рис. 11 различимы две кратные донные волны на 33 мс. и 47 мс.

2. Суммирование с ослаблением кратных волн

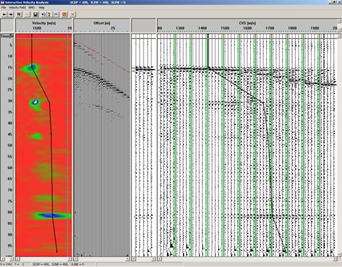
При проведении пикирования скоростей, показанном на рис. 12, имеется возможность уменьшить влияние кратных волн в суммированном временном разрезе путём выбора скоростей, при которых кратные волны не вносят существенного вклада в конечную сумму.

Рис. 11. Пикирование скоростей с целью подавления кратных волн.

Результат суммирования с выбранными скоростям представлен на рис. 12.

Рис. 12. Временной разрез с подавлением кратных волн.

3. Суммирование с усилением кратных волн

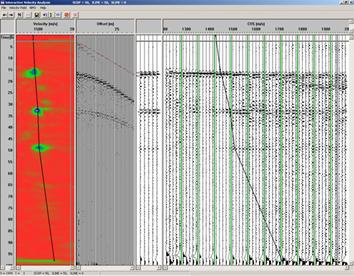
В качестве иллюстрации возможностей работы со спектром скоростей проведём суммирование с усилением кратных волн. Соответствующее пикирование показано на рис. 13.

Рис. 13. Пикирование скоростей с целью усиления кратных волн.

Результат суммирования с выбранными скоростям представлен на рис. 14.

Рис. 14. Временной разрез с усилением кратных волн.

4. Суммирование с заданными интервалами скоростей

В возможности суммирования также входит проведение суммирования с заданными интервалами постоянных скоростей. Выбор соответствующих интервалов и скоростей может быть произведён после визуального анализа картины спектра скоростей. Зададим интервалы постоянных скоростей – 1,5 км/с для времён 0-30 мс.;1,7 км/с для времён 30-100 мс. (Рис. 15).

Рис. 15. Задание интервалов с постоянной скоростью суммирования.

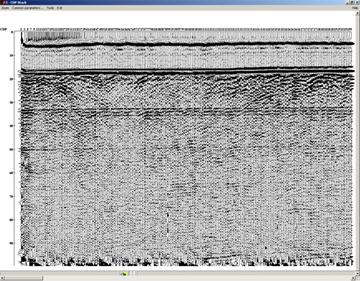
Результат суммирования представлен на рис. 16.

Рис. 16. Временной разрез с интервалами постоянства скорости суммирования.

При таком выборе скоростей заметно выделение нижней границы примерно на 80 мс.

Спектр скоростей является мощным современным инструментом для обработки сейсмической информации, требующий значительных вычислительных способностей. С его применением и варьированием значений скоростей возможно значительное улучшение временного разреза – выделение нужных границ, ослабление волн-помех.

Обрабатывающая система RadExPro предоставляет прекрасные возможности для реализации данного этапа обработки.

1. Сейсморазведка. Справочник геофизика / Под ред. И.И. Гурвича, В.П. Номоконова. — М.: “Недра”, 1981. — 464с.

2. Сейсморазведка. Учебное пособие / Гайнанов В. Г. — М.: Издательство МГУ, 2005. — 149 с.

3. Анализ данных сейсморазведки. Учебное пособие для студентов вузов / Бондарев В. И., Крылатков С. М. — Екатеринбург.: Издательство УГГГА, 2002. — 212с.

📹 Видео