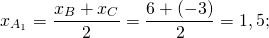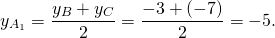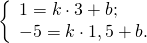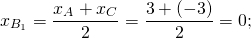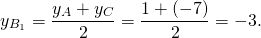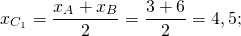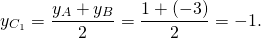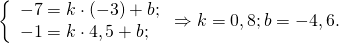Параметрическое уравнение медианы треугольника проведенной из точки

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составить уравнение медианы треугольника проведенной из вершины

УСЛОВИЕ:

5.3.18. Даны вершины треугольника А ( -3 ;2 ;8 ) , B ( -7 ;0 ;3 ) , С (3;4;5).
Составить параметрические уравнения его медианы, проведенной
из вершины А.

РЕШЕНИЕ ОТ u821511235 ✪ ЛУЧШЕЕ РЕШЕНИЕ

Добавил slava191 , просмотры: ☺ 2994 ⌚ 2018-08-23 14:57:00. математика 10-11 класс

Решения пользователей

Написать комментарий

Делим обе части равенства на π

и умножаем на 4

+pi k, k in Z
Можно правую часть записать в виде двух ответов:

x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].

x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]

[b]x=-5 – наибольшее отрицательное [/b]

О т в е т. x=1+8n in Z или x=3+ 8n, n in Z

корни чередуются так:

. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .

[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)

a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член

4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0

5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.

∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.

складываем оба равенства:

2* ∠ А=126 градусов.

По формулам приведения:

sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1

sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1

sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z

Найдем корни, принадлежащие указанному отрезку с помощью неравенства:

-286 ° ≤ 90 ° +360 ° *k ≤ 204 °

-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °

-376 ° ≤ 360 ° *k ≤ 114 °

Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]

Значит, указанному отрезку принадлежат два корня:

x=90 ° +360 °* ([green]-1[/green])=-270 °

x=90 ° +360 °*[red]0[/red]=90 °

7. KT- средняя линия трапеции:

Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)

Высоты треугольников АКО и СОК равны половине высоты трапеции

S_( Δ АКО)+S_( Δ COK)=44

S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=

О т в е т. [b]176[/b]

B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Видео:Уравнения стороны треугольника и медианыСкачать

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

🔍 Видео

Параметрические уравнения прямойСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

§49 Параметрические уравнения прямойСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Вычисляем высоту через координаты вершин 1Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

9 класс, 7 урок, Уравнение прямойСкачать

11. Прямая в пространстве и ее уравненияСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать