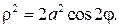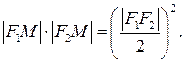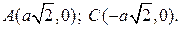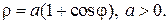Кардиоида
Лемниската Бернулли
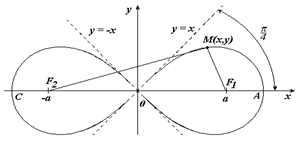
Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
Укажем, что точка М лежит на кривой, если выполнено условие
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
В полярных координатах
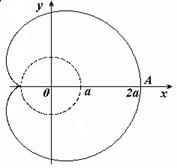
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 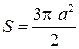
- 6. Параметрическое задание линий
- Содержание
- Параметрическое представление функции [ править | править код ]
- Параметрическое представление уравнения [ править | править код ]
- Параметрическое уравнение [ править | править код ]
- Примеры [ править | править код ]
- Уравнения некоторых кривых в параметрической форме:
- Уравнение окружности по заданному центру и радиусу в различных формах
- Уравнение окружности по заданному центру и радиусу в различных формах
- Центр окружности
- Уравнение окружности
- Общее уравнение окружности
- Стандартное уравнение окружности
- Параметрическое уравнение окружности
- Уравнение окружности в полярных координатах
- Параметрическое уравнение окружности в параметрической форме
- Уравнение окружности по заданному центру и радиусу в различных формах
- Уравнение окружности по заданному центру и радиусу в различных формах
- Центр окружности
- Уравнение окружности
- Общее уравнение окружности
- Стандартное уравнение окружности
- Параметрическое уравнение окружности
- Уравнение окружности в полярных координатах
- Параметрическое задание кривой
- Параметрическое задание кривой
- Уравнение окружности в параметрическом виде
- 6. Параметрическое задание линий
- Содержание
- Параметрическое представление функции [ править | править код ]
- Параметрическое представление уравнения [ править | править код ]
- Параметрическое уравнение [ править | править код ]
- Примеры [ править | править код ]
- Уравнения некоторых кривых в параметрической форме:
Видео:Физика - движение по окружностиСкачать

6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
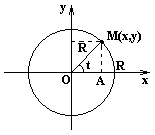 |
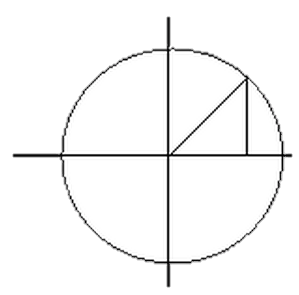
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox 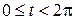
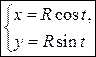
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
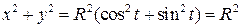
| | | следующая лекция ==> | |
| Четырехлепестковые розы | | | Астроида |
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Содержание
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Параметрическое представление функции [ править | править код ]
Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы
;> 
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] :
y = ψ ( θ ( x ) ) = f ( x )
и производная функции может быть вычислена как
y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= >
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.
Видео:Физика 9 класс. Движение по окружностиСкачать

Параметрическое представление уравнения [ править | править код ]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Параметрическое уравнение [ править | править код ]
Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.
x = x ( t ) ; y = y ( t ) 

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры [ править | править код ]
Уравнение окружности имеет вид:
x 2 + y 2 = r 2 . +y^ =r^ .>
Параметрическое уравнение окружности:
;> 
Параметрическое уравнение правой ветви гиперболы :
t> 
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
А вертикальное перемещение:
Следовательно, расстояние от груза до земли в произвольный момент падения:
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
Попробуй обратиться за помощью к преподавателям
Видео:Урок 90. Движение по окружности (ч.2)Скачать

Уравнения некоторых кривых в параметрической форме:
- Окружность
Параметрические кривые окружности:
Рисунок 1. Окружность и ее параметрические кривые
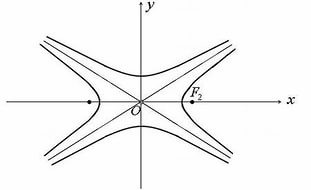
Уравнение гиперболы имеет вид:
Параметрические кривые гиперболы:
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
- Представим уравнение окружности в виде: [x^ +y^ =r^ ] [x^ +y^ =6^ ]
Значит, радиус $r$ равен 6.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Записать уравнение гиперболы в параметрическом виде.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Уравнение окружности по заданному центру и радиусу в различных формах
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Видео:Урок 89. Движение по окружности (ч.1)Скачать

Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности 1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Видео:Кинематика точки Движение по окружностиСкачать
Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Видео:Физика, Динамика, Движение по окружностиСкачать

Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Видео:Вращательное движение. 10 класс.Скачать

Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
Видео:Ускорение при равномерном движении по окружностиСкачать

Параметрическое уравнение окружности в параметрической форме
Видео:ЕГЭ ПО МАТЕМАТИКЕ | ДВИЖЕНИЕ ПО ОКРУЖНОСТИ | +1 БАЛЛ ЗА 5 МИНУТ |Скачать
Уравнение окружности по заданному центру и радиусу в различных формах
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Видео:Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности 1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Видео:Физика | Равномерное движение по окружностиСкачать

Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Видео:Кинематика. Движение по окружности. Урок 4Скачать

Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Видео:Лекция 6.1 | Описание движения по окружности | Александр Чирцов | ЛекториумСкачать

Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
Видео:Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Параметрическое задание кривой














Параметрическое задание кривой
- Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что
установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием
So например, эквационный х = 2Т г = 3Т-2(1) Людмила Фирмаль
2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом
примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для
- любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется
параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция Людмила Фирмаль
и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат
(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2) х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими
уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,
изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти
параметрическое уравнение эллипса (3) Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным
параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид) (5) * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно
изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).
Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6) U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7) — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если
вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)
и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные
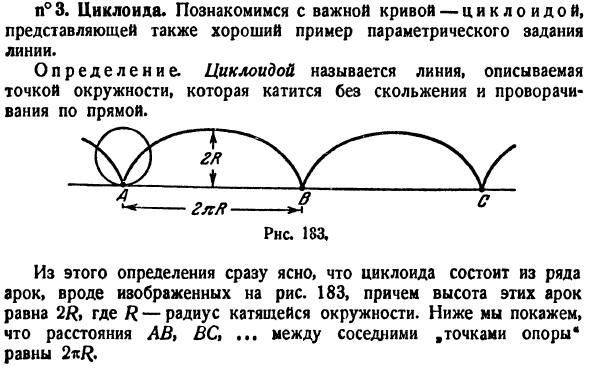
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как
показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат
возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной
к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.
(8) Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )) При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем
к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10) Если
сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае
t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение
проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое
уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-
точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,
нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f > = » K0(13) В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте
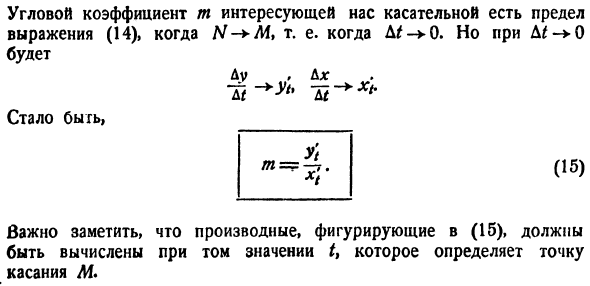
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является
пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД: (15 )) Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16) Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.
Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.
Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =
.Где f (/j u f ( / ) имеет непрерывную производную、 а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть
x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),
а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных
вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18) Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление
кривой х =(* + 3Т + л> г = 2Т * — (21) В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ 0, кривая точки M (21) направлена вогнутой поверхностью вверх.



















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнение окружности в параметрическом виде
Кардиоида
Лемниската Бернулли
Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
Укажем, что точка М лежит на кривой, если выполнено условие
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
В полярных координатах
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 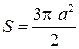
6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
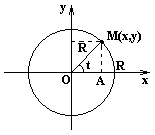 |
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox 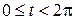
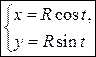
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
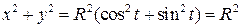
| | | следующая лекция ==> | |
| Четырехлепестковые розы | | | Астроида |
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Содержание
Параметрическое представление функции [ править | править код ]
Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы
;> 
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] :
y = ψ ( θ ( x ) ) = f ( x )
и производная функции может быть вычислена как
y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= >
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.
Параметрическое представление уравнения [ править | править код ]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Параметрическое уравнение [ править | править код ]
Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.
x = x ( t ) ; y = y ( t ) 

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры [ править | править код ]
Уравнение окружности имеет вид:
x 2 + y 2 = r 2 . +y^ =r^ .>
Параметрическое уравнение окружности:
;> 
Параметрическое уравнение правой ветви гиперболы :
t> 
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
А вертикальное перемещение:
Следовательно, расстояние от груза до земли в произвольный момент падения:
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
Попробуй обратиться за помощью к преподавателям
Уравнения некоторых кривых в параметрической форме:
- Окружность
Параметрические кривые окружности:
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
Параметрические кривые гиперболы:
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
- Представим уравнение окружности в виде: [x^ +y^ =r^ ] [x^ +y^ =6^ ]
Значит, радиус $r$ равен 6.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Записать уравнение гиперболы в параметрическом виде.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь