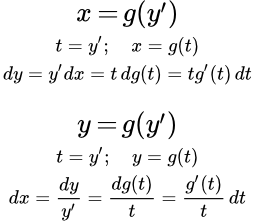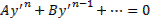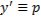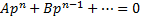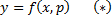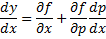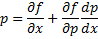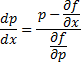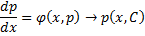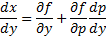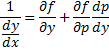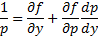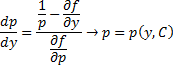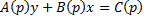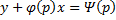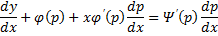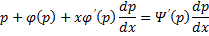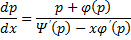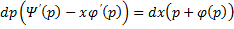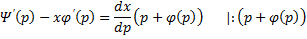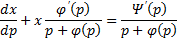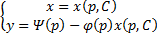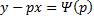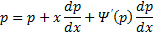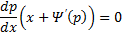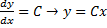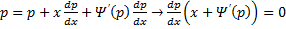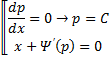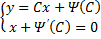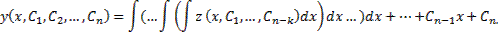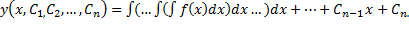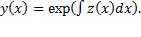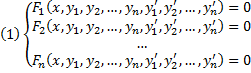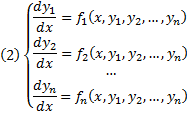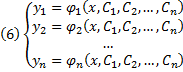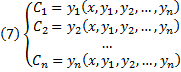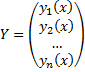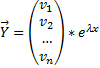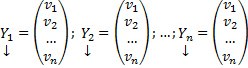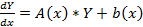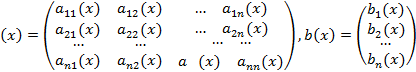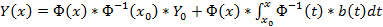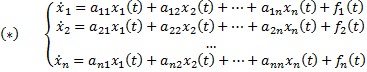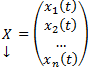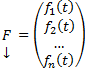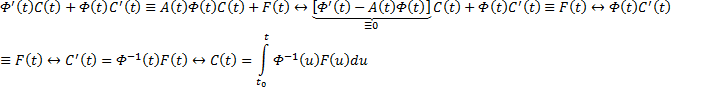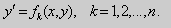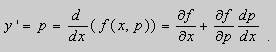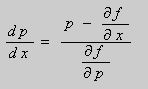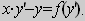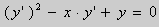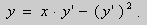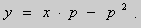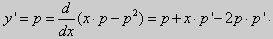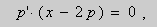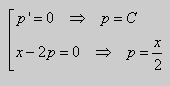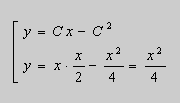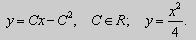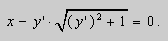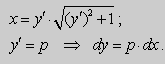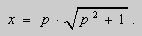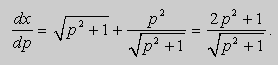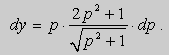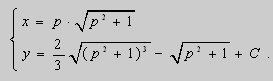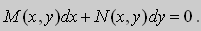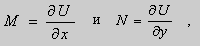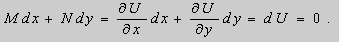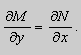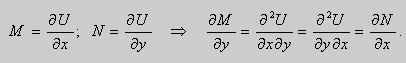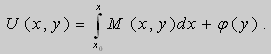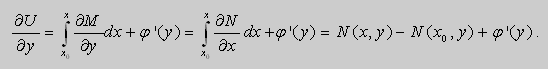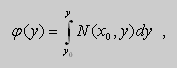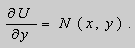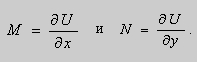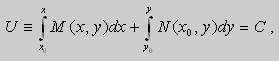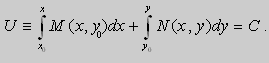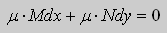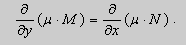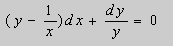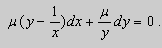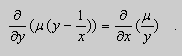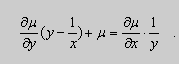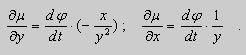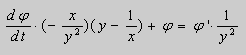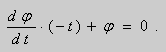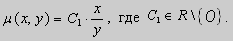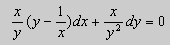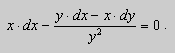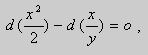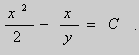Параметрический метод решения дифференциального уравнения (7 видео)

Дифференциальные уравнения, не содержащие одну из переменных

Содержание

Постановка задачи
Общий метод решения
Уравнения, разрешенные относительно переменной
Пример
Уравнения, не разрешенные относительно переменной
Пример
Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .
📸 Видео

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Постановка задачи

Здесь мы рассматриваем метод решения уравнений вида:
(1) ;
(2) .
То есть это дифференциальные уравнения первого порядка, не разрешенные относительно производной, и которые не содержат одну из переменных в явном виде.

Видео:ПАРАМЕТРИЧЕСКИЙ метод решения диффуров ОБОШЕЛ избранниц холостяка | Дифференциальные уравненияСкачать

Общий метод решения

Решение таких уравнений мы ищем в параметрическом виде. Пусть – параметр. Тогда переменные и являются функциями от этого параметра :
;
.
Производная также является функцией от параметра :
.

Преимущество параметрического представления заключается в том, что его можно создать многими способами. В качестве примера рассмотрим функцию
.
В параметрическом виде ее можно представить так:
.
Или так:
.
То есть мы можем найти бесконечно много способов, чтобы создать параметрическое представление для одной и той же функции.

Мы будем использовать это преимущество параметрического представления при решении уравнений (1) и (2). Общий метод заключается в том, чтобы подобрать такую функцию , чтобы уравнения (1) или (2) можно было разрешить относительно переменной или .

Рассмотрим уравнение (1):
(1) .
Пусть мы подобрали такую функцию , что при подстановке в (1), уравнение (1) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :
.
Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:
.
Интегрируя, получаем параметрическое представление для :
.

Теперь рассмотрим уравнение (2):
(2) .
Пусть мы подобрали такую функцию , что при подстановке в (2), уравнение (2) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :
.
Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:
.
Интегрируя, получаем параметрическое представление для :
.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Уравнения, разрешенные относительно переменной

Рассмотрим наиболее простой случай, когда исходное уравнение
(1)
удается разрешить относительно переменной :
.
В этом случае проще положить . Тогда .

Тогда имея две функции и , мы можем найти :
;
.

Аналогично, если исходное уравнение
(2)
удается разрешить относительно переменной :
.
То положим . Тогда .

Имея две функции и , мы можем найти :
;
.

Пример

Решить уравнение:
(1.1)

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде, введя параметр . Это уравнение разрешено относительно переменной . Поэтому делаем подстановку:
(1.2) .
Тогда
(1.3) .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной :
.
Отсюда получаем дифференциал переменной :
(1.4) .
Распишем дифференциал , используя (1.3):
;
(1.5) .
Подставляем (1.2) и (1.5) в (1.4):
.
Интегрируем:
.

Итак, мы получили решение в параметрическом виде:
(1.6) ;
(1.3) .

Далее мы можем явно выразить y через x. Для этого перепишем уравнение (1.6):
.
Решаем квадратное уравнение:

.
Заменим постоянную :
:
.
Подставляем в (1.3):

Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Уравнения, не разрешенные относительно переменной

Теперь рассмотрим более общий случай. Рассмотрим уравнение (1):
(1) .
Если это уравнение не удается разрешить относительно переменной , то у нас нет гарантий, что мы можем получить решение. Но мы можем попытаться найти такую функцию
, чтобы подставив в (1), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :
;
.
Подставляя их в выражение для дифференциала

и интегрируя, мы найдем .

Аналогично поступаем для уравнения (2):
(2) .
Нашей задачей является найти такую функцию
, чтобы подставив в (2), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :
;
.
Подставляя их в выражение для дифференциала

и интегрируя, мы найдем .

Пример

Решить уравнение:
(2.1) .

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде. Нашей задачей является найти такую подстановку , чтобы из уравнения (2.1) можно было выразить переменную через параметр .

Можно увидеть, что такой подстановкой является
(2.2) .
Подставляем в исходное уравнение (2.1):
;
;
;
(2.3) .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной и выразим его через параметр .
.
Подставим (2.2):
.
Здесь – функция от , определяемая из (2.3).
Интегрируем по частям и подставляем (2.3):
;
;
.

Автор: Олег Одинцов . Опубликовано: 22-08-2012 Изменено: 01-04-2016

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .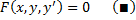

Уравнения первого порядка n-ой степени решаются так:

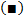
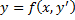
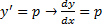
Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим , получим:

Продифференцируем по x:

Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: 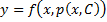. Это и будет решение.

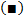
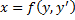
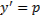
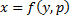
Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть . Вводим параметр , получаем . Дифференцируем по y обе части:

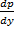
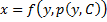
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: 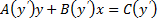. Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр 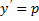, получаем:

Пусть 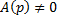, поделим всё выражение на A(p):

Продифференцируем по x:

Получили линейное уравнение первого порядка. Отсюда находим .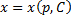

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :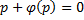

Если это тождество, то есть 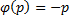, то:

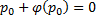
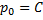
Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть , тогда – решение.

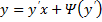
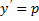
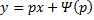
Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр , получаем . Дифференцируем по x, получаем:

Общее решение уравнения Клеро:

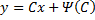
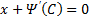
Здесь – семейство всевозможных кривых; – огибающая этого семейства, тоже является решением и называется особое решение.

Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.

Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y ‘(x), y »(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y(n) = f(x, y, y ‘, y », … , y(n − 1)).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1.

Общим решением дифференциального уравнения F(x, y(x), y ‘(x), y »(x), … , y(n )(x)) = 0 называется функция y = Ф(x, С1, С2, … , Сn), содержащая некоторые постоянные (параметры) С1, С2, … , Сn, и обладающая следующими свойствами:

Ф(x, С1, С2, … , Сn) является решением уравнения при любых допустимых значениях С1, С2, … , Сm;

для любых начальных данных y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1, для которых задача Коши имеет единственное решение, существуют значения постоянных С1 = A1, С2 = A2, … , Сn = An, такие что решение y = Ф(x, A1, A2, …, An) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С1, С2, . Сn) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

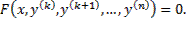
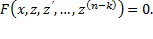
К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка: Если z = z(x,C1. Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле

Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной — уравнения вида F(y, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(y). После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции — уравнения вида F(x, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(x). После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение: F(x, p, p’, . p(n — 1)) = 0. Если правая часть уравнения F(x, y, y ‘. y(n) ) = 0, удовлетворяет условию однородностиF(x, ty, ty ‘. ty(n) ) = tk F(x, y, y ‘. y(n) ) то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой

Выражение для первой производной от y(x) не содержит производной от z(x):

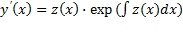
Поэтому, заменив в исходном уравнении y, y ‘. y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл.

Совокупность соотношений вида:

Где y1, y2, …, yn искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка.

Будем предполагать функции F2, F2, …, Fn такими, что система разрешима относительно производных от искомых функций:

Такие системы называются нормальными системами дифференциальных уравнений.

Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Семейство решений системы (2), зависящее от n произвольных постоянных C1, C2, …, Cn

называют обычно общим решением этой системы.

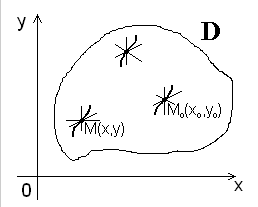
Дадим определение общего решения системы (2) в области D изменения переменных x, y1, y2, …, yn.

В качестве области D будем рассматривать область в пространстве (x, y1, y2, …, yn), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2).

Совокупность n функций (6), определённых в некоторой области изменения переменных x, C1, C2, …, Cn, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C1, C2, …, Cn в области D, так что при любых значениях x, y1, y2, …, yn, принадлежащих области D, системой (6) определяются значения C1, C2, …, Cn:

и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C1, C2, …, Cn, доставляемых формулами (7), когда точка (x, y1, y2, …, yn) пробегает область D.

Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C1, C2, …, Cn,, включая бесконечности, будет частным решением.

Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение.

1-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y1, …, yn любым частным решением этой системы она обращается в постоянную.

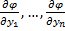
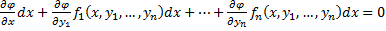
2-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), имеющая непрерывные частные производные по x, y2, …, yn, и такая, что в рассматриваемой области не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:

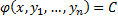
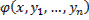
Равенство , где – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).

Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y1, y2, …, yn, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D.

Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ.

Система обыкновенных дифференциальных уравнений вида:

называется линейной системой. При система становится однородной. В векторно-матричной форме: , где
,

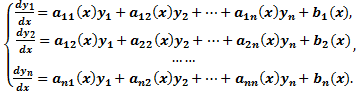
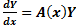
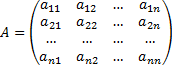
Будем искать решение 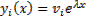. Ищем решение системы в таком виде:

Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций.

Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: .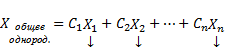

Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ.

Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка

Здесь 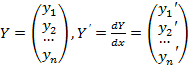A

Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ.

Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы 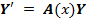, то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид:

где C — произвольный постоянный вектор-столбец, x0 — произвольная фиксированная точка из отрезка [a, b].

Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши.

Решением задачи Коши 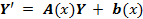, Y(x0) = Y0 является вектор-функция

Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ.

Определение системы неоднородных линейных ОДУ. Система ОДУ вида:

называется линейной неоднородной. Пусть

Система (*) в векторно-матричном виде: 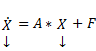. — система однородная, иначе – неоднородная.

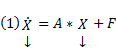
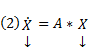
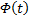
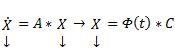
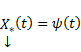
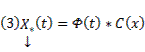
Сам метод. Пусть имеется линейная неоднородная система , тогда — линейная однородная система, соответствующая линейной неоднородной. Пусть – фундаментальная матрица системы решений, , где C – произвольный постоянный вектор, — общее решение системы. Станем искать решение системы (1) в виде , где C(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество:

(произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x0, 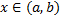– любые.

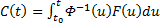
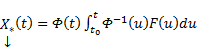
Видим, таким образом, что если в (3) в качестве C(t) брать , то вектор-функция будет решением системы (1).

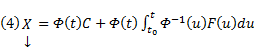
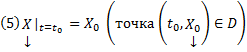
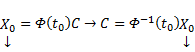
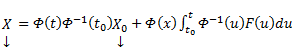
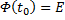
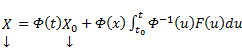
Общее решение линейной неоднородной системы (1) может быть записано в виде . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию . Подстановка (4) начальных данных (5) даёт . Следовательно, решение задачи Коши (1)-(5) может быть записано в виде: . В частном случае, когда , последняя формула принимает вид: .

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

Рассмотрим уравнение вида

F ( x , y , y ‘ ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений

Геометрически это означает , что в каждой точке 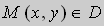задаётся несколько направлений поля (см.рис.2).

Следовательно через любую точку M ( x , y ) может проходить несколько интегральных кривых 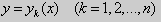. Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку M₀ ( x₀ , y₀) , надо помимо значений ( x₀ , y₀ ) дополнительно задать в этой точке направление поля y ‘ ( x₀) = y ‘_{0 .}

Задача Коши . Найти решение 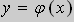уравнения F ( x , y , y ‘ ) = 0, удовлетворяющее начальным условиям y ( x₀) = y₀ и y ‘ ( x₀) = y ‘₀, где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0.

Теорема существования и единственности решения задачи Коши.

Пусть в некоторой окрестности U точки (x₀ , y₀ , y ‘₀), где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0, выполнены условия :

1) F( x , y , y ‘ ) определена, непрерывна и имеет непрерывные частные производные F’_y и F’_{y ‘} по совокупности переменных ( x , y , y ‘ ) ;

2) значение производной F_y‘_‘ (x₀ , y₀ , y’₀)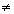0.

Тогда в некоторой окрестности точки x₀ существует единственное решение 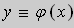уравнения F (x, y, y’) = 0, удовлетворяющее условиям y(x₀) = y₀ и y’ (x₀) = y’₀.

Метод введения параметра.

На практике при решении уравнений F( x , y , y ‘ ) = 0 часто используют следующий метод.

Предположим , что уравнение F( x , y , y ‘ ) = 0 “легко” решить относительно y : y = f ( x , y ‘ ). Тогда введем замену y ‘ = p ( параметр зависит от x ). Предполагая, что дифференциальное уравнение имеет решение y = y ( x ) , получим ( в силу уравнения )

Из этих равенств выражаем :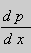

Это уравнение разрешено относительно производной 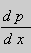. Пусть его общее решение имеет вид p = p ( x , C ) .Тогда общее решение заданного уравнения можно записать в виде y =f ( x , p ( x , C ) ). Решение найдено.

Таким методом можно решать , в частности , уравнения Лагранжа и Клеро.

Уравнение вида 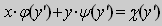называется уравнением Лагранжа. Оно является линейным относительно переменных x и y . Частным случаем этого уравнения является уравнение Клеро. Оно имеет вид :

Пример 1 . Решить уравнение

Решение. Выразим из уравнения (5) переменную y :

.Заменим 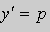и получим

Продифференцируем его по x :

Из этих равенств получаем :

После подстановки этих выражений в (6) будем иметь

Ответ :

Этим методом можно также решать уравнения , в которых «легко» выражается переменная x . Рассмотрим

Пример 2 . Решить уравнение

Решение . Выразим из уравнения (7) переменную x и введём параметр p :

Продифференцируем уравнение (8) по p :

Отсюда в силу равенства dy = p dx получим :

Проинтегрируем это уравнение :

Таким образом , с учётом ( 8 ) , получаем общее решение в параметрическом виде :

Примеры. Решить уравнения :

Уравнения в полных дифференциалах.

Если в уравнении (9) функции

В этом случае уравнение (9) называют уравнением в полных дифференциалах. После интегрирования получим общее решение уравнения

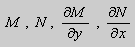
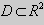
Теорема 1. Пусть функции непрерывные в некоторой односвязной области . Тогда необходимым и достаточным условием того, что уравнение (9) — в полных дифференциалах , является условие

Доказательство. 1. Необходимость.

Если выбрать функцию 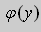та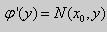к, чтобы

то и , следовательно ,

Таким образом , в уравнении (9)

Теорема 1 доказана.

Из теоремы следует , что общее решение уравнения (9) можно записать в виде

если 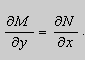Функцию U можно также представить в виде

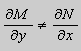
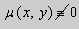
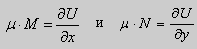
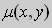
Предположим , что . Тогда можно попытаться найти такую функцию , чтобы . Функция называется интегрирующим множителем . В этом случае мы получаем уравнение

в полных дифференциалах. Следовательно, в силу теоремы 1,

Это уравнение позволяет найти интегрирующий множитель. Рассмотрим

Пример. Решить уравнение

Решение. Простой проверкой убеждаемся , что (10) не является уравнением в полных дифференциалах. Умножим его на неизвестную функцию :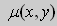

Попробуем найти 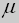из уравнения :

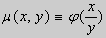
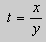
Пусть . Обозначим через и получим

После подстановки этих выражений в (11) будем иметь :

Проинтегрируем полученное уравнение :

Таким образом, интегрирующий множитель можно взять в виде

Умножим теперь уравнение (10) на функцию

Теорема 2. Если функции M и N непрерывные , имеют непрерывные частные производные первого порядка по x и по y , и 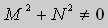, то интегрирующий множитель существует.

Замечание. Точка ( x₀ , y₀ ), в которой M ( x₀ , y₀ ) = N ( x₀ , y₀ ) = 0 является особой точкой уравнения (9). Поведение решений в окрестности особой точки изучается в лекции 3.

Примеры. Решить дифференциальные уравнения :