Падение потенциала в диффузной части дэс уравнение

План лекции:

Видео:СТРОЕНИЕ МИЦЕЛЛЫ - урок 1Скачать

ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ

На поверхности твердого тела при его контакте с жидкостью самопроизвольно возникает избыточный электрический заряд, который компенсируется противоионами. В результате, на границе Ж-Т возникает ДЭС. Образование ДЭС происходит самопроизвольно, вследствие стремления поверхностной энергии к минимуму и в связи с особыми свойствами границы раздела.

Возникновение на границе электрических зарядов характерно, прежде всего, для золей и суспензий, дисперсная фаза которых формируется из твердых частиц.

При погружении металла в раствор электролита, содержащего ионы этого металла, устанавливается электрохимическое равновесие. Если химический потенциал ионов металла m _М больше химического потенциала этих же ионов в растворе m _р , то ионы переходят из металла в раствор, и поверхность металла заряжается отрицательно. И, наоборот, при помещении медной пластинки в раствор сульфата меди с достаточно высокой концентрацией соли, металлическая поверхность заряжается положительно.

Возникновение зарядов на твердом теле приводит к тому, что на границе раздела фаз возникает электрический потенциал, обозначаемый через j .

Если j -потенциал определяется активностью ионов в растворе, то есть твердое тело играет роль электрода, то для выражения его можно воспользоваться уравнением Нернста:

(5.1)

где n — заряд иона, F — число Фарадея, а_п и а_р -активности ионов у поверхности и в растворе.

Видео:Падение потенциала вдоль проводникаСкачать

ОБРАЗОВАНИЕ ДЭС

Поверхность твердого тела приобретает ионы определенного знака. Эти ионы называют потенциалоопределяющими. К твердой поверхности из жидкой среды притягиваются ионы противоположного знака, их называют противоионами. Возникает ДЭС.

Было предложено несколько теорий образования ДЭС.

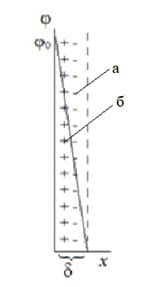
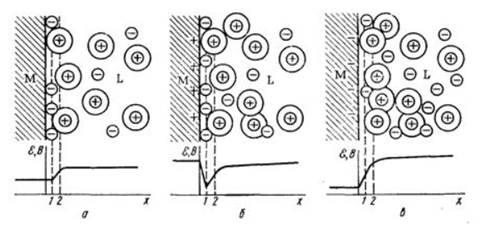
Простейшей из них является модель плоского конденсатора Гельмгольца (5.1.а), согласно которой потенциалоопределяющие ионы и противоионы находятся на молекулярном расстоянии друг от друга, взаимодействие между ними осуществляется только за счет электростатических сил, а падение потенциала между слоями происходит линейно.

Дальнейшее развитие теория ДЭС получила в работах Гуи и Чепмена на основе сопоставления электростатического взаимодействия противоионов с энергией их теплового движения. Согласно модели Гуи и Чепмена противоионы рассматриваются как точечные заряды, не имеющие собственных размеров, расположенные в диффузном слое (5.1.б), а потенциал экспотенциально снижается по мере удаления от поверхности.

Согласно теории Штерна , которую можно рассматривать как основу современного представления о структуре ДЭС (5.1.в), противоионы находятся в двух положениях: одна их часть образует адсорбционный слой (иногда его называют плотным слоем или слоем Гельмгольца).Другая часть противоионов находится в диффузном слое. В отличии от адсорбционного слоя противоионы диффузного слоя не закреплены, в результате диффузии и взаимного отталкивания они способны перемещаться в пределах диффузного слоя в глубь жидкости.

ДЭС может возникнуть на частицах, находящихся в полярной среде, и в отсутствии электролитов, вследствие ориентации диполей, а также частичной поверхностной диссоциации полярных частиц, если в жидкой среде присутствуют хотя бы следы воды.

Потенциал, возникающий на границе между адсорбционным и диффузным слоем, называется потенциалом диффузного слоя j _д .

Толщина адсорбционного слоя d определяется размерами противоионов, обычно она незначительна и не превышает 1 нм. В диффузном слое противоионы движутся хаотично, их положение изменяется. По этой причине толщина диффузного слоя будет величиной приведенной l .

Видео:Электрокинетический потенциалСкачать

ТЕРМОДИНАМИЧЕСКИЕ СООТНОШЕНИЯ МЕЖДУ ПОВЕРХНОСТНЫМ НАТЯЖЕНИЕМ И ЭЛЕКТРИЧЕСКИМ ПОТЕНЦИАЛОМ ДЭС.

Образование ДЭС происходит самопроизвольно, в результате стремления

системы уменьшить энергию Гиббса поверхностного слоя.

Обозначим изменение электрической энергии через j d q ( j — электрический потенциал ДЭС, q — заряд поверхности).

Тогда, в соответствии с обобщенным уравнением первого и второго начал термодинамики (без учета химической энергии), изменение энергии Гиббса на поверхности можно записать следующим образом:

dG = — S dT + s dS + j d q (5.2)

s dS — изменение поверхностной энергии

dG = s dS + j d q (5.3)

Полный дифференциал энергии Гиббса :

dG = s dS +S d s + j d q + q d j

Вычитая это уравнение из 5.3, получим:

S d s + q d j = 0 (5.4)

Разделим 5.4 на S (площадь межфазной поверхности) и обозначим q / S через q_S (плотность заряда), получим:

(5.5)

I уравнение Липпмана

Если знаки потенциала и заряда совпадают, то поверхностное натяжение уменьшается с увеличением потенциала, если их знаки противоположны, то с увеличением потенциала увеличивается поверхностное натяжение.

Дифференциальная емкость ДЭС, как и любого конденсатора, определяется соотношением:

(5.6)

Дифференцируем 5.5 по j и подставляем в него соотношение 5.6, получаем второе уравнение Липпмана:

(5.7)

II уравнение Липпмана

Это уравнение показывает возможность определения емкости ДЭС, если известна зависимость поверхностного натяжения от потенциала.

Если ДЭС возникает вследствие перераспределения ионов, то для описания адсорбции ионов можно воспользоваться адсорбционным уравнением Гиббса. Если на поверхности адсорбируется катионы:

Г₊ — гиббсовская адсорбция потенциалоопределяющих катионов.

Поверхностная плотность заряда:

Подставляем это выражение в уравнение Липпмана:

сравниваем 5.8 и 5.9:

(5.10)

a _o и a_p — активности иона на поверхности и в растворе

Полученное уравнение называется уравнением электродного потенциала Нернста. Приведенный вывод указывает на связь между уравнениями Гиббса и Липпмана и показывает, что потенциалоопределяющие ионы, адсорбируясь, изменяют поверхностное натяжение.

Видео:Метод потенциалов собственной поляризацииСкачать

СПЕЦИФИЧЕСКАЯ АДСОРБЦИЯ ИОНОВ

Штерн попытался учесть влияние специфической адсорбции ионов на электрический потенциал, обусловленный действием ковалентных сил дополнительно к электростатическим силам. Так как радиус действия сил такой адсорбции соизмерим с размером ионов, это дает основание учитывать ковалентные силы только для ионов, входящих в плотный слой Гельмгольца.

Плотность поверхностного заряда противоионов можно разделить на две части: плотность заряда q_r, обусловленную слоем Гельмгольца и q _d диффузного слоя Гуи.

Общая поверхностная плотность заряда ДЭС:

Штерн предположил, что поверхность имеет определенное число адсорбционных центров, каждый из которых взаимодействует с одним противоионом.

Константа такой квазихимической реакции равна фактору Больцмана, в котором общий адсорбционный потенциал составляет сумму адсорбционных потенциалов электростатического и специфического взаимодействия:

(5.12)

F n j — электростатический адсорбционный потенциал,

F — потенциал специфической адсорбции.

Такой подход позволил Штерну получить уравнение для плотности поверхностного заряда в слое Гельмгольца:

(5.13)

где q ¥ — предельно возможная плотность поверхностного заряда

x_o — мольная доля противоионов в растворе.

При малых концентрациях электролита можно пренебречь единицей в знаменателе.

Теория Штерна позволяет рассчитать заряд в плотном и диффузном слоях.

Из теории Ш. следует, что лучше адсорбируются и ближе подходят к Пв менее гидратированные ионы.

Специфическая адсорбция зависит от сродства адсорбируемых ионов к поверхности, их способности образовывать недиссоциирующие поверхностные соединения. Большими адсорбционными потенциалами обладают многозарядные ионы (Al 3+ , Th 4+ и др.), органические ионы.

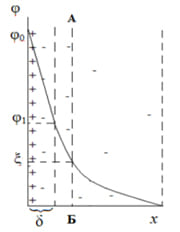
Сильно адсорбирующиеся ионы в плотном слое способны создать избыточный заряд со знаком заряда противоионов. Это явление называется перезарядкой. (рис. 5.2)

Рис. 5.2. Изменение потенциала поверхности при ее перезарядке.

При перезарядке j _o и j _d имеют разные знаки. Общую поверхностную плотность заряда можно представить в виде разности между величинами адсорбции потенциалоопределяющих ионов разного знака :

Пример:

1) водный р-р — поверхность AgI. При избытке в растворе Ag + (при добавлении AgNO₃ ) эти ионы являются потенциалоопределяющими

В роли противоионов выступают NO₃ — , часть которых, находится в плотном слое, часть — в диффузном.

Ф — ла ДЭС :[AgI]m · nAg + |(n — x)NO₃ — |x NO ₃ —

n­-число потенциалопределяющих ионов

x-число противоионов в диффузной части

Если в систему с AgI добавить KNO₃ , то потенциалопределяющими станут иодид — ионы:

[ AgI ] m · nI — |( n — x ) K + | x K +

2) В ДЭС на поверхности оксидов в растворе в качестве потенциалопределяющих ионов выступают Н + или OH — (в зависимости от среды).

В результате преобладающей адсорбции одного и этих ионов поверхность оксида приобретает соответствующий знак заряда поверхности. Например: SiO₂ обладает кислотными свойствами, поэтому его поверхность заряжена отрицательно:

[SiO₂]m · nOH — |(n — x)H + |x H +

FeO имеет основные свойства, его поверхность будет заряжена положительно:

[FeO]m · nH + |(n — x)OH — |x OH —

Al₂O₃ — в кислой среде поверхность заряжена положительно, в щелочной — отрицательно.

В дисперсионных системах ДЭС возникает на поверхности частиц.

Частицу дисперсной фазы в гетерогенно-дисперсной системе вместе с ДЭС называют мицеллой.

Строение мицеллы можно показать той же формулой, что и строение ДЭС.

Внутренняя части мицеллы — агрегат основного вещества, на поверхности агрегата — потенциалопределяющие ионы:

Агрегат + потенциалопределяющие ионы = ядро.

Ядро + противоионы = гранула.

Гранулу окружают противоионы диффузного слоя. Вся мицелла электронейтральна.

Мицеллы создают в дисперсионной системе соответствующую противоионам ионную среду — суспензионный эффект. Если противоионами являются Н + и ОН — — ионы, то среда приобретает соответственно кислый или щелочной характер. При удалении частиц, например, фильтрацией, противоионы уходят вместе с ними в количествах, эквивалентных заряду частиц. Отсюда суспензионный эффект количественно можно определить как разность между концентрационными характеристиками противоионов в суспензии (дисперсионной системе) и в фильтрате. При определении кислотно-основных свойств дисперсной фазы суспензионный эффект рассчитывается по соотношению:

рН_сэ = рН_с — рН_ф, то есть по разности значений рН суспензии и фильтрата. Суспензионный эффект возрастает с увеличением концентрации дисперсной фазы, с увеличением ее дисперсности, и уменьшается с повышением концентрации электролита (это связано со сжатием ДЭС).

Видео:2.1. Электрокинетические свойства дисперсных системСкачать

Теория Гельмгольца – Перрена

Впервые гипотезу о существовании двойного слоя высказал Г. Квинке, пытаясь объяснить открытое им явление потенциала протекания. Однако, первая теория строения двойного электрического слоя (ДЭС) предложена Германом Гельмгольцем в 1879 г. Последующее развитие этих представлений проведено Жаном Батистом Перреном (1904 г).

Согласно теории Гельмгольца – Перрена, заряды располагаются на межфазной границе в виде двух рядов ионов, подобно плоскому конденсатору, одна обкладка которого образована потенциалопределяющими ионами, вторая – противоионами (рис. 4, а). Толщина ДЭС при этом близка к размерам сольватированных ионов или молекул. Потенциал в ДЭС линейно уменьшается с расстоянием, как в плоском конденсаторе. Плотность поверхностного заряда η₀ , в соответствии с теорией плоского конденсатора, определяется уравнением:

, (2)

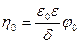
где δ – толщина ДЭС, ε₀ε – диэлектрическая проницаемость среды между обкладками конденсатора, εε₀/δ=С – емкость плоского конденсатора, φ₀ – потенциал поверхности относительно объёма раствора (где потенциал равен нулю).

Теория Гельмгольца-Перрена находится в качественном согласии с рядом экспериментальных фактов: заряд двойного слоя в первом приближении можно считать линейно меняющимся в зависимости от потенциала; на основе теории можно приближенно оценить емкость двойного слоя. Однако, теория не учитывает зависимости ёмкости и заряда поверхности от концентрации электролита и температуры, что на практике имеет место. Кроме того, в результате гидродинамических исследований было обнаружено, что при взаимном перемещении твердой и жидкой фаз вместе с твердой частицей движется слой жидкости, превышающий толщину ДЭС по теории Гельмгольца – Перрена. Это означает, что за границей слоя Гельмгольца, а именно в плоскости скольжения должна существовать некоторая доля нескомпенсированного заряда поверхности, которая является движущей силой при электрофорезе и электроосмосе. Представления о ДЭС как плоском конденсаторе не могли объяснить электрокинетические явления.

Рис. 4. Схемы строения двойного электрического слоя по теории:

а) Гельмгольца – Перрена; б) Гуи – Чэпмена; в) Штерна

Теория Гуи – Чэпмена

В 1910 г. французский физик Луи Гуи, (выдвинувший впервые предположение о тепловой природе броуновского движения) и не зависимо от него в 1913 г. английский физик Сидни Чэпмен, предложили более сложную структуру двойного слоя, представив, что слой противоионов имеет размытое, диффузное строение (рис. 4, б) и обусловлен противоположно направленным действием двух факторов: сил электростатического притяжения со стороны потенциалопределяющих ионов и теплового движения ионов (диффузией). В результате устанавливается динамическое равновесие, при котором концентрация противоионов в диффузном слое уменьшается с расстоянием от поверхности по закону Больцмана:

, (3)

где — концентрация i— иона в ДЭС на расстоянии х от поверхности; — концентрация i- иона за пределами ДЭС, в объёме раствора; Z – заряд иона; F – число Фарадея; φ – потенциал на расстоянии х от поверхности; R – универсальная газовая постоянная; Т – абсолютная температура. Уравнение записано для положительно заряженных противоионов (Z > 0, φ

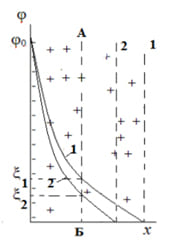
Поскольку ξ – потенциал является частью общего падения потенциала в двойном электрическом слое φ₀ , становится понятно различие действия ряда факторов на ξ и φ₀ –потенциалы. Рассмотрим, например, как влияет повышение концентрации индифферентного электролита на структуру ДЭС. Индифферентным является электролит, который не взаимодействует с поверхностью частицы, не влияет на заряд поверхности, а следовательно и на φ₀. Но введение индифферентного электролита повышает концентрацию противоионов в диффузном слое. А поскольку на компенсацию поверхностных зарядов потенциалопределяющих ионов необходимо то же количество противоионов, что и до введения электролита, часть противоионов оказывается лишней и граница двойного слоя сдвигается ближе к поверхности, толщина диффузного слоя уменьшается, потенциал на плоскости скольжения, т.е. ξ- потенциал, — уменьшается (рис. 5). При достаточно большой концентрации электролита граница двойного слоя может совпасть с плоскостью скольжения и ξ- потенциал станет равен нулю. Частицы перестанут перемещаться в электрическом поле. Такое состояние называется изоэлектрическим (изоэлектрическая точка). Чем больше заряд ионов в диффузном слое, тем интенсивнее их влияние на ξ- потенциал.

Модель диффузного слоя Гуи – Чэпмена явилась значительным достижением в теории двойного электрического слоя. Позже подобные физические представления легли в основу модели ионной атмосферы теории сильных электролитов Дебая и Гюккеля.

Рис. 5. Смещение границы ДЭС (пунктирные линии 1 и 2) и изменение кривой распределения потенциала в двойном электрическом слое (кр.1 и 2) при добавлении индифферентного электролита

Важным достижением теории явилось количественное выражение зависимости поверхностной плотности заряда η₀ от потенциала поверхности φ₀ и концентрации электролита в объёме раствора с (уравнение Гуи – Чэпмена). При выводе количественных соотношений ионы рассматривались как точечные заряды, равномерно «размазанные» по поверхности, а концентрация любых ионов в диффузном слое на расстоянии х от поверхности частицы выражается уравнением Больцмана (3). В присутствии нескольких электролитов в диффузном слое, объёмная плотность заряда ρ (Кл/м 3 ) на расстоянии х от поверхности:

(5)

или, с учетом уравнения Больцмана (3):

(6)

Для сферических частиц объёмная плотность заряда ρ_x связана с потенциалом φ уравнением Пуассона:

, (7)

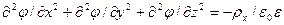
где x, y и z – пространственные координаты, ε₀ε – абсолютная диэлектрическая проницаемость, ε – относительная диэлектрическая проницаемость среды, ε₀ – диэлектрическая постоянная, равная 8,854·10 -12 Ф/м. Если радиус кривизны поверхности много больше толщины двойного электрического слоя, то двойной электрический слой можно считать плоским и учитывать изменение потенциала только по одной координате, x:

(8)

Подставив (6) в уравнение (8), получим уравнение Пуассона — Больцмана:

(9)

После двойного интегрирования уравнения Пуассона – Больцмана получают уравнение, выражающее закон изменения потенциала как функцию расстояния от поверхности и свойств раствора, в том числе, от концентрации электролита.

Уравнение (9) лежит в основе теории двойного электрического слоя. Известно несколько способов интегрирования уравнения (9), которые отличаются выбором конкретных граничных условий.

Первое интегрирование уравнения Пуассона – Больцмана (9) в пределах от 0 до φ для случая, когда раствор представляет собой бинарный симметричный электролит, т.е. i=2, c₀₊=c_0-=c , z₊=z_—=z приводит дифференциальному уравнению:

(10)

Анализ уравнения (10) показывает, что при увеличении концентрации электролита и валентности противоионов производная dφ/dx возрастает, что означает более резкое падение потенциала в двойном электрическом слое и, следовательно, снижение ξ – потенциала. Таким образом, теория Гуи – Чэпмена объясняет падение ξ – потенциала при увеличении концентрации противоионов и увеличении их заряда.

Уравнение (10) позволяет связать потенциал поверхности φ₀ с поверхностной плотностью заряда η₀. Учитывая, что условие электронейтральности ДЭС можно выразить соотношением η₀ и объёмной плотности заряда ρ:

, (11)

и подставив далее ρ в (11) из (8), при условии x=0 получим

(12)

Подстановка (10) в (12) и интегрирование при условии φ=φ₀ при x=0 приводит к уравнению Гуи — Чэпмена:

(13)

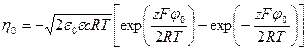
Первое интегрирование уравнения Пуассона – Больцмана (9) при условии малых потенциалов(много меньше 25 мВ) приводит к следующему результату[1]:

ǽ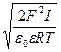φ_{x ,} (14)

ǽ= , (15)

— ионная сила раствора по теории растворов электролитов Дебая – Гюккеля.

Интегрируя уравнение (14) в пределах от 0 до x и от φ₀ до φ_x , получим:

Уравнение (16) показывает, что потенциал уменьшается в ДЭС по экспоненте с ростом расстояния.

Важным свойством ДЭС является его ёмкость. Различают понятия дифференциальная dη₀/dφ₀ и интегральная η₀/φ₀ ёмкость. При небольших потенциалах они примерно равны. Ёмкость ДЭС, вычисленная из уравнения (13), оказывается в десятки раз выше измеренной экспериментально. Причина состоит в том, что теория Гуи – Чэпмена не учитывала размер ионов, рассматривая их как точечные заряды, которые могут подходить вплотную к поверхности. Теория Гуи – Чэпмена имела ещё ряд недостатков. Так, например, теория не могла учесть различное влияние ионов одинаковой валентности, но разных радиусов на ДЭС: эффективность действия ионов на практике возрастает с увеличением их радиуса. Не возможно было в рамках этой теории объяснить и явление перезарядки ДЭС (смены знака ξ –потенциала) под влиянием многовалентных противоионов. Кроме того, теория была не применима к концентрированным растворам электролитов. Все эти недостатки были учтены в теории Штерна, которая явилась новым этапом в развитии представлений о двойном электрическом слое.

Теория Штерна

В 1924 г. немецкий физик Отто Штерн ввел два новых условия в представления о структуре ДЭС, что привело по сути к созданию новой современной теории строения двойного электрического слоя.

Согласно первому условию, введенному Штерном, ионы рассматривались не как точечные заряды (в предыдущих теориях), а имели конечные радиусы. Поэтому противоионы не могут подойти к поверхности ближе, чем сумма радиусов потенциалопределяющих ионов и ближайших к поверхности гидратированных противоионов (десятые доли нанометра). Вторым условием, введенным Штерном, является учет, дополнительно к электростатическому взаимодействию противоионов с заряженной поверхностью, энергии специфического адсорбционного притяжения противоионов к поверхности.

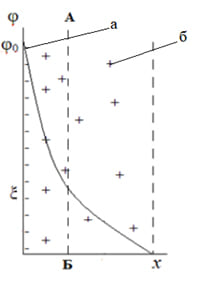
Схема строения ДЭС по теории Штерна как бы объединяет две предыдущие теории, вводя представления о плотном слое (слой Гельмгольца, или адсорбционный слой, или слой Штерна) и диффузном слое (слой Гуи), рис. 4 в. Часть противоионов, притягиваясь к заряженной потенциалопределяющими ионами поверхности электростатическими и адсорбционными силами, образует с потенциалопределяющими ионами плотный слой – плоский конденсатор (слой Гельмгольца). Внешняя обкладка его находится в плоскости наибольшего приближения к поверхности (x=δ). Считается, что она проходит через центры тяжести зарядов противоионов, ближайших к поверхности. В плотном слое потенциал падает с расстоянием от поверхности практически по прямой, как в плоском конденсаторе (φ₀-φ₁). Остальные противоионы, в количестве необходимом для полной компенсации поверхностного заряда, образуют диффузный слой, в котором потенциал падает по экспоненте от φ₁ до φ=0. Плоскость скольжения АБ расположена в диффузной части ДЭС. Изменение равновесных концентраций катионов С₊ и анионов С_— в ДЭС на различных расстояниях от поверхности показано на рис. 6.

Уравнения (5)-(9) справедливы и для теории Штерна, появляется только новое граничное условие: распределение зарядов противоионов рассматривается как функция расстояния не от x=0, а от x=δ, поэтому вместо (4) необходимо применить граничное условие x=δ, φ=φ₁. Поскольку интегрирование при этом условии включает все противоионы, уравнение (10) справедливо во всей области x 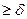. Вместо уравнения (13) в этом случае справедливо уравнение:

(17)

В уравнении (17) плотность поверхностного заряда η₀ выражена как функция потенциала φ₁ в плоскости максимального приближения противоионов и равновесной концентрации электролита в растворе с.

Рис.6. Распределение концентраций анионов и катионов в ДЭС при отрицательно заряженной поверхности. С₀ – концентрация в растворе

Потенциал на внешней плоскости слоя Гельмгольца играет важную роль как в коллоидной химии, так и в электрохимии.

Следует заметить, что уравнения, описанные выше, не учитывают адсорбционных сил, а лишь электростатические взаимодействия противоионов с потенциалопределяющими ионами. Эту часть теории Штерна называют модифицированной теорией Гуи, а уравнение (17) — уравнением Гуи.

Если в уравнении (16) расстояние отсчитывать не от поверхности твердой фазы, а от начала диффузной части ДЭС, то вместо (16) получим:

Согласно известным математическим правилам, показатель степени экспоненты в уравнении (18) должен быть безразмерной величиной, следовательно, параметр ǽ должен иметь размерность, обратную единице длины. Величину 1/ǽ = λ называют приведенной толщиной диффузной части двойного электрического слоя.Если в уравнении (18), x =λ=1/ǽ, то φ=φ_δe -1 . Таким образом, λ – это расстояние, на котором потенциал диффузной части ДЭС снижается в e раз (е=2,718…). Для разбавленных растворов электролитов λ составляет десятки нанометров, что много больше размеров ионов. Как видно из (15), приведенная толщина диффузной части ДЭС обратно пропорциональна заряду иона и корню квадратному из концентрации электролита. С ростом температуры растет энергия теплового движения, а с увеличением диэлектрической проницаемости среды усиливается диссоциация электролитов. Оба фактора увеличивают толщину ДЭС.

Большой заслугой теории Штерна является учет специфических (адсорбционных) взаимодействий противоионов с поверхностью. Оно характерно для адсорбции многовалентных ионов, ионов красителей, алкалоидов, ПАВ. Для учета специфической адсорбции Штерн ввёл понятие адсорбционного потенциала иона (Ф_i), выражающего изменение потенциальной энергии системы при переносе 1 г-моля ионов из глубины раствора в поверхностный слой за счет адсорбционных сил в отсутствие электрической работы, т.е. это дополнительная к кулоновской энергия адсорбции иона. При этом силы притяжения считаются отрицательными, а отталкивания – положительными. Заряд слоя противоионов состоит из заряда плотного слоя η_Г и диффузного η_д:

Заряд слоя Гельмгольца (плотного слоя), по теории Штерна, складывается из заряда ионов, адсорбированных как за счет электростатического адсорбционного потенциала zFφ₁, так и за счет потенциала специфической адсорбции Ф_i. При этом предполагалось, что поверхность имеет определенное число адсорбционных центров, каждый из которых взаимодействует с одним противоионом. Максимальное число центров Г_∞ соответствует заряду η_∞=zFГ_∞. Константа такой квазихимической реакции может быть выражена через работу адсорбции по аналогии с константой адсорбционного равновесия в теории Лэнгмюра:

(20)

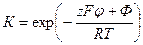
Здесь общий адсорбционный потенциал представлен как сумма адсорбционных потенциалов электростатического и специфического взаимодействий. Такой подход позволил Штерну получить уравнение для плотности поверхностного заряда в слое Гельмгольца:

, (21)

x₀ – мольная доля противоионов в растворе.

Таким образом, теория Штерна, позволяет рассчитать заряд в плотном и диффузном слоях. На практике, при малой специфической адсорбции и в отсутствии её, применяют уравнение (17), а при значительной адсорбции (21). Расчет емкости двойного электрического слоя для различных концентраций электролитов с учетом этих уравнений дает удовлетворительное согласие с результатами экспериментальных измерений.

Теория Штерна позволила решить ряд вопросов, ответы на которые не дали предыдущие теории ДЭС. Так же, как и теория Гуи-Чэпмена, теория Штерна объясняет влияние индифферентных электролитов на структуру ДЭС, но кроме того, теория Штерна объясняет влияние неиндифферентных электролитов (параграф 4). Теория Штерна объясняет также влияние противоионов одинакового заряда, но разных радиусов: специфическая адсорбционная способность ионов обусловлена их поляризуемостью и гидратацией, поэтому ионы с бóльшим радиусом лучше адсорбируются, а следовательно уменьшают толщину ДЭС, так как ион за счет адсорбционных сил ближе подходит к поверхности. Учет адсорбционных сил позволил объяснить явление перезарядки ДЭС под действием многозарядных противоионов и ряд других факторов (параграф 4).

Вклад в дальнейшее развитие теории ДЭС внесли многие ученые. В 1947 г. Дональд Грэм предложил специфически адсорбированные ионы в плотном слое считать приближенными к поверхности на меньшие расстояния, вследствие частичной дегидратации, введя понятие внутренней плоскости Гельмгольца.Ещё более сложные модели учитывают диффузное распределение заряда и потенциала не только в жидкой фазе, но и в приповерхностном слое твердой фазы (внутренней обкладке ДЭС). Для ионных кристаллов это связано с изменением энергии образования дефектов кристаллической структуры вблизи поверхности (ионов внедрения и вакансий); для высокополимерных ионитов (имеющих сетчатую структуру) и пористых, гелеобразных слоёв, характерных для стёкол, — с адсорбцией ионов, постепенно уменьшающейся вглубь твердой фазы.

Теоретические представления о строении ДЭС развиваются, совершенствуются и чрезвычайно широко используются при решении многих практических и теоретических задач, в том числе в коллоидной химии. Например, в учении об агрегативной устойчивости дисперсных систем.

Видео:Матвеенко В. Н. - Коллоидная химия - Электрические свойства дисперсных системСкачать

Двойной электрический слой (ДЭС): понятие и теории строения

Содержание:

Видео:4 3 Электрохимический потенциалСкачать

1. Электрокинетические явления.

В начале XIX века Рейс, проводя электролиз воды, обнаружил явления электрокинетики.

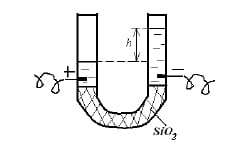
В одном из опытов Рейсс заметил, что если дно U-образной трубки наполнить кварцем, то при наложении разности потенциалов на систему совершается смещение столба воды в область «-» электрода. Явление получило название электроосмос.

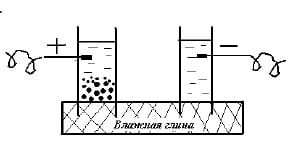
После этого Рейс сделал схему из двух стеклянных трубок, заполненных водой и опущенных концами в мокрую глину. Под действием электрического тока глина передвигалась к электроду, имеющему заряд «+», что получило название «электрофорез».

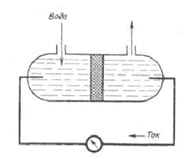
А уже после Рейсса явлениями электрокинетики занялся Г. Квинке. Он открыл потенциал течения — разность потенциалов появлялась при просачивании воды сквозь песок, глину или другую пористую диафрагму.

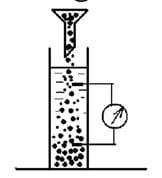
В 1879 г. Дорном был открыт потенциал седиментации. Разность потенциалов возникала, когда частички кварца свободно осаждались в столбе жидкости.

Все эти явления объединяло одно — либо разность потенциалов вызывала движение фаз, либо, наоборот, движение фаз создавало разность электрических потенциалов. По этому признаку рассмотренные явления и получили общее название «электрокинетические».

Итак, различают электрокинетические явления двух родов:
• I рода, в которых происходит взаимное перемещение фаз при воздействии электрического поля;
• II рода, в которых разность потенциалов возникает за счет перемещения двух фаз.

Присутствие одноименно заряженных частиц на поверхности дисперсной фазы и противоположно заряженных частиц на поверхности дисперсной среды и есть причина возникновения электрокинетических явлений. Совокупность же всех зарядов, сконцентрированных на границе раздела фаз, образует структуру, называемую двойным электрическим слоем (ДЭС).

Видео:Электродные потенциалы металлов. Электроды сравненияСкачать

2. Механизмы образования ДЭС.

Формирование ДЭС происходит в результате стремления системы уменьшить энергию Гиббса межфазного слоя. Межфазный слой – это слой, в котором происходит взаимодействие двух различных фаз, в результате соприкосновения которых свойства поверхности каждой фазы станут отличаться от их индивидуальных свойств.

Различают два типа ДЭС, в которых:

• заряды распространяются в различных фазах (пограничный);
• заряды располагаются на плоскости одной из фаз (поверхностный).

ДЭС будет играть весомую роль при:

• переносе вещества или энергии;
• ионном обмене;
• электрокаппилярных и элктрокинетических явлениях;
• адсорбции ионов.

Выделяют несколько механизмов образования ДЭС:

а) Формирование ДЭС при наступлении электрохимического равновесия, посредством прохода заряженных частиц между фазами. Основные разновидности этого механизма формирования ДЭС:

• Переход заряженных частиц на границе металл – газ. В этом варианте происходит переход электронов с поверхности металла в газовую фазу, из-за чего поверхность металла заряжается положительно, а со стороны газовой фазы образуется электронное облако. Появляется препятствие для дальнейшего перехода электронов (положительный заряд поверхности металла), в результате чего наступает равновесное состояние.

• В системе «малорастворимое соединение – жидкость» переход заряженных частиц будет происходить в результате поверхностного растворения частицы малорастворимого соединения, при чем в жидкую фазу преимущественно будет выполняться переход тех ионов, электрохимический потенциал которых выше. В данном случае равновесие будет выражаться электрохимическими потенциалами:

При установлении равновесия происходит переход ионов из фазы с большим электрохимическим потенциалом, в фазу с меньшим потенциалом. При этом возникает межфазный скачок потенциалов, который препятствует дальнейшему переходу ионов. В результате этого равновесие будет выражаться уравнением

• Ионизация молекул вещества твердой фазы может происходить за счет диссоциации поверхностных ионогенных групп под воздействием полярной дисперсной среды. К примеру, молекулы SiO₂ при взаимодействии с водой образуют кремниевую кислоту, которая после будет диссоциировать с переходом в раствор ионов Н + . В этом случае силикат-ионы образуют слой потенциалопределяющих ионов, а ионы Н + — слой противоионов.

б) ДЭС может формироваться за счет адсорбции ионов из раствора, этот механизм формирования можно разделить на несколько вариантов:

• В соответствии с правилом Фаянса – Панета ионы могут адсорбироваться на поверхности частиц, сообщая им соответствующий заряд, если эти ионы входят в состав кристаллической структуры этих частиц. Около заряженной поверхности будут концентрироваться противоположно заряженные ионы (противоионы).

• Заряд поверхности может образовываться за счет избирательной адсорбции ионов из растворов, не входящих в состав твердой фазы. В пример можно привести раствор хлорида натрия, в котором на металлах адсорбируются хлорид-ионы и придают его поверхности «-» заряд, а ионы натрия, в свою очередь, являются противоионами создавая с хлорид-ионами ДЭС

в) ДЭС может создаваться в том случае, если поверхность образована двумя фазами, молекулы которых не могут диссоциировать, но обладают дипольными моментами. Согласно правилу Кёна, из двух соприкасающихся фаз, не способных обмениваться зарядами, положительно заряжается та фаза, которая имеет большую диэлектрическую проницаемость.

Видео:Урок 231. Свойства электрического потенциалаСкачать

3. Модели строения двойного электрического слоя.

Авторы моделей придерживались следующих положений:

• На межфазной поверхности в системе «твердое вещество – жидкость», ДЭС образуется из потенциалопределяющих ионов, связанных с твердой поверхностью и эквивалентного количества противоионов, находящихся в жидкой дисперсной среде;
• Равномерное распределение заряда на поверхности твердой фазы;
• Одинаково заряженные частицы находятся в равновесии.

Основное различие между моделями строения ДЭС заключается в постепенном усложнении представлений о структуре слоя противоионов.

3.1 Модель Гельмгольца – Перрена.

В конце XIX века Г. Гельмгольц предложил первую модель строения ДЭС, далее ее развивал Ж.Б. Перрен, но уже в 1904 г.
Модель Гельмгольца – Перрена основывалась на представлении ДЭС как плоского конденсатора, в котором обкладки представлялись как два ряда ионов (потенциалопределяющих ионов и противоионов) (рисунок 1). Потенциал в ДЭС линейно уменьшался с расстоянием, как в плоском конденсаторе, а плотность заряда на поверхности η₀ определялась уравнением:

где:
δ – толщина ДЭС;
ε₀ε – диэлектрическая проницаемость среды между обкладками конденсатора;
(ε₀ε /δ)= С – емкость плоского конденсатора;
φ₀ – потенциал поверхности относительно объема раствора.

Рисунок 1. Схема строения двойного электрического слоя по модели Гельмгольца – Перрена: а) слой потенциалопределяющих ионов, б) слой противоионов.

Модель Гельмгольца – Перрена подтверждена несколькими экспериментальными фактами:

• В зависимости от потенциала заряд ДЭС можно считать линейно меняющимся;
• Модель позволяет количественно оценить емкость ДЭС.

У этой модели есть и ряд недостатков:

• Не учитывается зависимость емкости и заряда поверхности от концентрации электролита и температуры;
• При взаимном перемещении твердой и жидкой фаз вместе с твердой частицей движется слой жидкости, превышающий толщину ДЭС по теории Гельмгольца – Перрена;
• Не объясняет электрокинетические явления.

3.2 Модель Гуи – Чапмена.

В начале XX века Л. Гуи и С. Чампен (Чэпмен) предположили более сложную структуру ДЭС (рисунок 2), предположив, что слой противоионов имеет диффузное строение и обусловлен противоположно направленным действием двух факторов:

• Сил электростатического притяжения со стороны потенциалопределяющих ионов;
• Направленного диффузионного действия.

Рисунок 2 — Схема строения двойного электрического слоя по модели Гуи – Чэпмена: а) слой потенциалопределяющих ионов, б) слой противоионов.

По закону Больцмана концентрация противоионовв диффузном слое изменяется, за счет установления динамического равновесия:

где:
c_iX – концентрация i-иона в ДЭС на расстоянии xот поверхности;
c_i0 – концентрация i-иона за пределами ДЭС;
Z – заряд иона;
F – число Фарадея (96500);
φ – потенциал на расстоянии x от поверхности;
R – универсальная газовая постоянная (8,31);
Е – абсолютная температура.

Если взять в пример плоский конденсатор (модель Гельмгольца – Перрена), то все противоионы будут располагаться около поверхности (при температуре близкой к абсолютному нулю), так как диффузность слоя будет определяться тепловым движением ионов.

Вторая представленная модель позволила описать явления электрокинетики. При перемещении твердой и жидкой фаз относительно друг друга плоскость скольжения (АБ) лежит внутри двойного слоя, поэтому на границе скольжения φ≠0. Потенциал в плоскости скольжения соответствует той доле заряда поверхности, которая нескомпенсирована противоионами и вызывает перемещение фаз при наложении электрического поля. Часть общего скачка потенциала в двойном электрическом слое, которая приходится на границу скольжения и проявляется в электрокинетических явлениях, называется электрокинетическим, или ξ – потенциалом.

Можно описать изменение структуры ДЭС при повышении концентрации индифферентного электролита (рисунок 3). Введение индифферентного электролита повышает концентрацию противоионов в диффузном слое. Но, так как на компенсацию поверхностных зарядов потенциалопределяющих ионов необходимо то же количество противоионов, что и до введения электролита, часть противоионов окажется в избытке и это приведет к таким изменениям как:

• Граница ДЭС сдвинется ближе к поверхности;
• Слой Гуи уменьшится;
• Электрокинетический потенциал уменьшится.

Рисунок 3 — Смещение границы ДЭС (пунктирные линии 1 и 2) и изменение кривой распределения потенциала в двойном электрическом слое (кривые 1 и 2) при добавлении индифферентного электролита.

При описании данной модели Гуи и Чапмену удалось сделать важное открытие — они смогли определить концентрацию электролита в объеме раствора с и потенциал поверхности φ₀ в зависимости от плотности заряда η₀. В уравнении количество ионов в слое Гуи, определяется уравнением Больцмана (2), также ионы были рассмотрены как точечные заряды. В присутствии нескольких электролитов в диффузном слое, объёмная плотность заряда ρ (Кл/м 3 ) на расстоянии х от поверхности:

или, с учетом уравнения Больцмана (2):

Если ДЭС считать плоским и учитывать изменение потенциала только по одной координате, х, то:

Подставив (4) в уравнение (5), получим уравнение Пуассона – Больцмана:

В основе данной модели лежит уравнение (6), так как из него можно получить уравнение, выражающее зависимость потенциала от свойств и концентрации электролита:

При двойном интегрировании уравнения (6) в пределах от 0 до х и от φ₀ до φ_х, получаем:

С увеличением расстояния потенциал ДЭС уменьшается по кривой, это определяется уравнением (8).

Емкость ДЭС разделяют на:

• дифференциальную dη0/dφ0
• интегральную η0/φ0.

Недостатки модели Гуи-Чапмена:

• Не учитывала увеличение эффективности действия ионов при увеличении их радиуса;
• Не могла объяснить перезарядку ДЭС;
• Не подходит для определения ДЭС в концентрированных растворах.

Все эти недостатки были учтены в теории Штерна, которая стала новым этапом в развитии представлений о двойном электрическом слое.

3.3 Модель Штерна.

Дальнейшее изучение строения ДЭС проводил физик О.Штерн, который ввел два условия о его структуре:

• Ионы он представлял как частицы имеющие конечные радиусы;
• Учет энергии специфического адсорбционного притяжения противоионов к поверхности.

В своей схеме Штерн объединил две прошлые модели и ввел представления о плотном и диффузионном слое (рисунок 4). Часть противоионов, притягиваясь к заряженной потенциалопределяющими ионами поверхности электростатическими и адсорбционными силами, образует с потенциалопределяющими ионами плотный слой – плоский конденсатор. В плотном слое потенциал падает с расстоянием от поверхности практически по прямой, как в плоском конденсаторе. Остальные противоионы, в количестве необходимом для полной компенсации поверхностного заряда, образуют диффузный слой, в котором потенциал падает по экспоненте от φ₁ до φ=0. Плоскость скольжения АБ расположена в диффузной части ДЭС.

Рисунок 4 — Схема строения двойного электрического слоя по модели Штерна

Уравнения (3) – (6) так же применимы и для модели Штерна, но возникает еще одно условие: функция расстояния х= δ описывает распределение противоионов.

После интегрирования уравнения Пуассона – Больцмана в этом случае справедливо уравнение:

Данные уравнения не берут во внимание адсорбционные силы, а выражение (9) называется уравнением Гуи. И если расстояние отсчитывать от начала диффузионного слоя ДЭС, то уравнение (8) преобразуется в:

С ростом температуры растет энергия теплового движения, а с увеличением диэлектрической проницаемости среды усиливается диссоциация электролитов. Оба фактора увеличивают толщину ДЭС.

В отсутствии электрического поля происходит перенос ионов на поверхность под влиянием адсорбционных сил, такое явление Штерн назвал адсорбционным потенциалом иона (Ф_i). Это считается главным достижением данной модели.

По модели Штерна плотный слой заряжается за счет заряда ионов при адсорбции:

• Электростатического адсорбционного потенциала z_i Fφ₁;
• Специфической адсорбции Фi.

При учете этих факторов Штерн вывел уравнение для плотного слоя Гельмгольца:

Таким образом, модель Штерна позволяет рассчитать заряд как в плотном, так и в диффузионном слое.

Модель Штерна позволила решить ряд вопросов, ответы на которые не смогли дать предыдущие теории строения ДЭС:

Зависимость структуры двойного слоя за счет введения не- и индифферентных электролитов;

• Зависимость от различного радиуса ионов;
• Дала понятие перезарядки.

3.4 Модель Грэма.

Грэм развил предыдущие модели и выделил три части в ДЭС (рисунок 5):

• Внутренний плотный слой (внутренняя плоскость Гельмгольца), образованная молекулами растворителя или активными поверхностными ионами. Если в этой плоскости находятся только молекулы растворителя, то заряд равен нулю, а если поверхностно-активные ионы -q₁.
• Внешняя плоскость Гельмгольца. Ее общий заряд равен q₂, а потенциал плоскости Ψ₂;
• Диффузионный слой, в котором Ψ₂ изменяется до нуля, а плотность заряда совпадает с q₂.

Рисунок 5 — Строение ДЭС по Грэму: а) поверхность металла не заряжена; б) поверхность металла заряжена положительно; в) поверхность металла заряжена отрицательно.

В первой плоскости Гельмгольца находятся только специфически адсорбирующиеся анионы, причем их поверхностная концентрация растет при переходе от незаряженной поверхности (рисунок 5, а) к заряженной положительно (рисунок 5, б). При достаточно отрицательном заряде поверхности (рисунок 5, в) во внутреннем слое Гельмгольца остается лишь растворитель, и заряд его становится равным нулю. В этих условиях ДЭС электрически равен двум последовательно включенным конденсаторам.

Грэм разработал метод расчета кривых емкости ДЭС, где dη₀/dφ₀ при различных концентрациях электролита, так как он посчитал, что данная ёмкость будет зависеть не от концентрации раствора.

Таким образом модель Грэма может рассматриваться как модель, отражающая основные черты и особенности структуры ДЭС «металл – электролит».

3.5 Модель Фрумкина при адсорбции органических веществ.

Модель Фрумкина была разработана в 1926 году, она была рассмотрена в целях определения формы электрокаппилярных кривых и влияния органических веществ на ДЭС.

Адсорбцию органических соединений можно рассматривать как замену в двойном слое воды на органическое вещество. Так как размеры органических молекул больше, чем молекул воды, то, как это следует из теории плоского конденсатора, удельная емкость воды будет больше емкости исходного вещества в растворе, такая замена вызывает необходимость отвода заряда с обкладок конденсатора.

В случае перехода от исходного раствора к раствору с органическим веществом возникает разность потенциала равная сдвигу потенциала на электрокаппилярной кривой. Все это происходит так как молекулы органического вещества обладают дипольным моментом.

По версии Фрумкина в данном случае двойной слой напоминает два параллельно присоединенных конденсатора (это является одним из его исходных положений). В одном из конденсаторов будет находиться вода, между обкладками, а у другого – органические вещества. Другое положение теории связано с выбором изотермы адсорбции.

В качестве еще одного исходного предположения Фрумкин допускает, что адсорбция органического вещества подчиняется уравнению Ленгмюра:

В согласии с законом распределения Больцмана, можно записать в виде:

Из основного уравнения электрокаппилярности следует, что снижение пограничного натяжения σ под влиянием адсорбции органического вещества при данном δ равно:

Из данных уравнений Фрумкин вывел уравнение новой изотермы:

Bc=θ/(1-θ) exp(-2aθ) (15)

а – константа аттракционного взаимодействия.

Полученное уравнение назвали изотермой Фрумкина.

3.6 Модель Алексеева–Попова–Колотыркина (АПК).

На случай смешанных растворов была разработана модель Алексеева – Попова – Колотыркина типа:

где:
A_* — — – поверхностно-активный анион, снижающий емкость плотного слоя по сравнению с той, которая наблюдается в присутствии поверхностно-неактивного аниона A — .

В 60-х годах ХХ века Пейн сделал открытие, которое не описывалось ни одним физическим явлением. В системах типа нитрата калия зависимость энергии от заряда носила линейный характер, но, если рассмотреть границу Hg/H₂О (xM NH₄NO₃ + (1–x)M NH₄F), то можно было увидеть, что эта зависимость приобретала параболический вид.

После 20 лет попыток решения этой проблемы был дан ответ. В смешенных растворах выделяют скачок потенциала, а не заряд электрода. Это легло в основу модели АПК.

В смешанных растворах с постоянной ионной силой типа:

где:
A_* — и A — – соответственно поверхностно-активный и поверхностно-неактивный анионы.

Анионы A_* — вытесняются из ДЭС только в том случае, когда емкость адсорбированных частиц больше емкости свободных частиц, но если эти емкости равны, то энергия будет иметь линейную зависимость.

При значениях m выше m≤0.2, отсутствуют экспериментальные данные для количественного определения адсорбции ионов.

При использовании модели АПК некоторые параметры находят из экспериментальных данных. При этом она очень хорошо описывает некоторые свойства ДЭС при специфической адсорбции, но только на идеально поляризуемых электродах.

Видео:В чем отличие ЭДС, Напряжение, Потенциал, Падение НапряженияСкачать

4. Влияние различных факторов на структуру ДЭС.

4.1 Влияние индифферентных и неиндифферентных электролитов.

Влияние концентрации индифферентного электролита на структуру ДЭС показано в разделе 3.2. При увеличении концентрации электролита увеличивается заряд противоионов, это приводит к уменьшению ξпотенциала. Учитывая все это уравнение (9) преобразуется в:

Уравнение (17) показывает, что при неизменном заряде поверхности η₀ увеличение концентрации индифферентного электролита с и заряда противоионов z приводит к снижению потенциала φ₁. При этом происходит уменьшение диффузионного слоя, снижение ξ-потенциала.

Неиндифферентным электролитом называют электролит, в котором хотя бы один ион может влиять на потенциал поверхности φ₀, то такой ион будет называться потенциалопределяющим. При увеличении заряда поверхности η₀, то также повышается и ξ-потенциал. Появление этих двух факторов приводит к зависимости ξ-потенциала от с: при малых с главным фактором является рост адсорбции потенциалопределяющих ионов, η₀ и ξ-потенциал растут, затем наступает насыщение поверхности, рост заряда прекращается и главным фактором выступает сжатие диффузного слоя за счет повышения концентрации противоионов, ξ-потенциал уменьшается.

4.2 Явление перезарядки ДЭС под влиянием многозарядных противоионов.

Явление перезарядки ДЭС возникает в плотном слое посредством того, что многозарядные анионы могут превысить заряд потенциалопределяющих ионов. Так как происходит перезарядка, то потенциалы в двух слоях ДЭС приобретают отличные друг от друга знаки. Так как происходит смена знаков потенциалов, то изменяется и ξ-потенциал. Вследствие этого явления изменяется направление движения частиц дисперсной фазы.

4.3 Влияние температуры, рН и других факторов.

Увеличение температуры приведет к нескольким факторам:

• Произойдет увеличение теплового движения, следовательно, так же увеличиться и толщина слоя Гуи;
• При увеличении температуры может произойти удаление адсорбированного ионов с поверхности из-за этого произойдет снижение потенциалов.

Если частицы образованы веществом, проявляющим кислотные или основные свойства, то в качестве потенциалопределяющих ионов могут выступать ионы Н + или ОН — , в зависимости от рН среды. Высокая адсорбционная способность ионов Н + (из-за малого радиуса) и ОН — (из-за большого дипольного момента) определяет влияние рН на φ₀. При адсорбции этих ионов из раствора ξ-потенциал растет за счет увеличения заряда поверхности и потенциала φ₀. Особо велико влияние рН среды в тех случаях, когда вещество твердой фазы обладает амфотерными свойствами. В этом случае при изменении рН возможна перезарядка поверхности.

Видео:Двойной электрический слой (задача 2)Скачать

5. Заключение.

Первой теорией строения ДЭС была теория Гельмгольца – Перрена: ДЭС состоит из двух плоских зарядов и взаимодействующих между собой только за счет электростатических сил притяжения. Структура подобна плоскому конденсатору, падение потенциала между слоями происходит линейно.

Модель Гуи – Чэпмена предполагала диффузное расположение противоионов, находящихся под воздействием сил, действующих в противоположных направлениях: электростатических сил притяжения и сил теплового движения ионов, приводящих к диффузии и размыванию внешнего слоя. Теория вводит понятие диффузионного слоя, ионы рассматриваются как точечные заряды, не имеющие собственных размеров.

По теории Штерна строение ДЭС представляется следующим образом: ионы входящие в состав твердой фазы, образуют внутреннюю обкладку двойного слоя; ионы противоположного знака образуют внешнюю обкладку, при этом часть противоионов находится в непосредственном соприкосновении с ионами твердой фазы, образуя плотный слой, другая часть — диффузионный слой.

Грэм усовершенствовал модель Штерна и разделил ДЭС на три части: внутренний плотный слой, или же внутренняя плоскость Гельмгольца, внешний плотный слой и диффузионный слой. В этом случае ДЭС представляется в виде двух последовательно соединенных конденсаторов.

Фрумкин изучал строение ДЭС при адсорбции органических соединений. В этом случае ДЭС представлял собой два параллельно подсоединенных между собой конденсатора, в одном из них между обкладками находятся молекулы воды, в другом – молекулы органического вещества.

📸 Видео

Матвеенко В. Н. - Коллоидная химия - Теория ДЛФОСкачать

МицеллаСкачать

Схема строения мицеллыСкачать

Электротонические потенциалы и потенциалы действияСкачать

3.1. Устойчивость и коагуляция дисперсных системСкачать

Электростатика | эквипотенциальные поверхностиСкачать

Потенциал электростатического поля, разность потенциалов | Физика 10 класс #50 | ИнфоурокСкачать

Дисперсные системы. Часть 1.Скачать