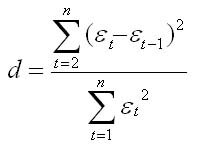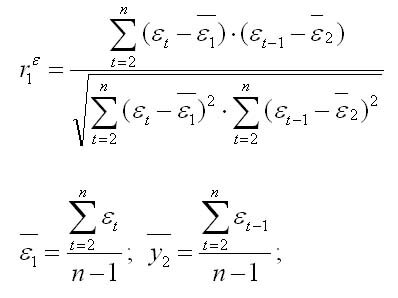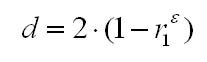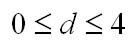Рассматриваем уравнение регрессии вида:
где k — число независимых переменных модели регрессии.
Для каждого момента времени t = 1 : n значение определяется по формуле
Изучая последовательность остатков как временной ряд в дисциплине эконометрика, можно построить график их зависимости от времени. В соответствии с предпосылками метода наименьших квадратов остатки должны быть случайными (а). Однако при моделировании временных рядов иногда встречается ситуация, когда остатки содержат тенденцию (б и в) или циклические колебания (г). Это говорит о том, что каждое следующее значение остатков зависит от предыдущих. В этом случае имеется автокорреляция остатков.
Видео:Лабораторная работа Прогнозирование по уравнению трендаСкачать

Причины автокорреляции остатков
Автокорреляция остатков может возникать по несколькими причинами:
Во-первых, иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения в значениях Y.
Во-вторых, иногда причину автокорреляции остатков следует искать в формулировке модели. В модель может быть не включен фактор, оказывающий существенное воздействие на результат, но влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Зачастую этим фактором является фактор времени t.
Иногда, в качестве существенных факторов могут выступать лаговые значения переменных, включенных в модель. Либо в модели не учтено несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или циклических колебаний.
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Методы определения автокорреляции остатков
Первый метод — это построение графика зависимостей остатков от времени и визуальное определение наличия автокорреляции остатков.
Второй метод — расчет критерия Дарбина — Уотсона
Т.е. Критерий Дарбина — Уотсона определяется как отношение суммы квадратов разностей последовательных значений остатков к сумме квадратов остатков. Практически во всех задачах по эконометрике значение критерия Дарбина — Уотсона указывается наряду с коэффициентом корреляции, значениями критериев Фишера и Стьюдента
Коэффициент автокорреляции первого порядка определяется по формуле
Соотношение между критерием Дарбина — Уотсона и коэффициентом автокорреляции остатков (r1) первого порядка определяется зависимостью
Т.е. если в остатках существует полная положительная автокорреляция r1 = 1, а d = 0, Если в остатках полная отрицательная автокорреляция, то r1 = — 1, d = 4. Если автокорреляция остатков отсутствует, то r1 = 0, d = 2. Следовательно,
Видео:Как определить автокорреляцию в остатках Дарбин УотсонСкачать

Алгоритм выявления автокорреляции остатков по критерию Дарбина — Уотсона
Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотеэы о наличии положительной или отрицательной автокорреляции в остатках. Затем по таблицам определяются критические значения критерия Дарбина — Уотсона dL и du для заданного числа наблюдений и числа независимых переменных модели при уровня значимости а (обычно 0,95). По этим значениям промежуток [0;4] разбивают на пять отрезков.
Если расчетное значение критерия Дарбина — Уотсона попадает в зону неопределенности, то подтверждается существование автокорреляции остатков и гипотезу отклоняют
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Если Вас интересует решение контрольных по эконометрике щелкните здесь
Видео:10-02 Критерий знаковСкачать

Тест Дарбина-Уотсона на наличие автокорреляции остатков
Тест Дарбина-Уотсона проводится с помощью трех калькуляторов:
- Парная регрессия
- Множественная регрессия
- Уравнение тренда (линейная и нелинейная регрессия)
Рассмотрим третий вариант. Линейное уравнение тренда имеет вид y = at + b
1. Находим параметры уравнения методом наименьших квадратов через онлайн сервис Уравнение тренда .
Система уравнений
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а 0 и подставим во второе уравнение
Получаем a0 = -12.78, a1 = 26763.32
Уравнение тренда
y = -12.78 t + 26763.32
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
, т.е. в 97.01% случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая.
| t | y | t 2 | y 2 | t ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y |
| 1990 | 1319 | 3960100 | 1739761 | 2624810 | 1340.26 | 18117.16 | 451.99 | 148.84 | 28041.86 |
| 1996 | 1288 | 3984016 | 1658944 | 2570848 | 1263.61 | 10732.96 | 594.99 | 38.44 | 31417.53 |
| 2001 | 1213 | 4004001 | 1471369 | 2427213 | 1199.73 | 817.96 | 176.08 | 1.44 | 16095.92 |
| 2002 | 1193 | 4008004 | 1423249 | 2388386 | 1186.96 | 73.96 | 36.54 | 0.04 | 7211.59 |
| 2003 | 1174 | 4012009 | 1378276 | 2351522 | 1174.18 | 108.16 | 0.03 | 0.64 | 210.94 |
| 2004 | 1159 | 4016016 | 1343281 | 2322636 | 1161.4 | 645.16 | 5.78 | 3.24 | 2786.55 |
| 2005 | 1145 | 4020025 | 1311025 | 2295725 | 1148.63 | 1552.36 | 13.17 | 7.84 | 4155.05 |
| 2006 | 1130 | 4024036 | 1276900 | 2266780 | 1135.85 | 2959.36 | 34.26 | 14.44 | 6614.41 |
| 2007 | 1117 | 4028049 | 1247689 | 2241819 | 1123.08 | 4542.76 | 36.94 | 23.04 | 6789.19 |
| 2008 | 1106 | 4032064 | 1223236 | 2220848 | 1110.3 | 6146.56 | 18.51 | 33.64 | 4758.73 |
| 20022 | 11844 | 40088320 | 14073730 | 23710587 | 11844 | 45696.4 | 1368.3 | 271.6 | 108081.77 |
Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i — e i-1 ) 2 |
| 1319 | 1340.26 | -21.26 | 451.99 | 0 |
| 1288 | 1263.61 | 24.39 | 594.99 | 2084.14 |
| 1213 | 1199.73 | 13.27 | 176.08 | 123.72 |
| 1193 | 1186.96 | 6.04 | 36.54 | 52.19 |
| 1174 | 1174.18 | -0.18 | 0.03 | 38.75 |
| 1159 | 1161.4 | -2.4 | 5.78 | 4.95 |
| 1145 | 1148.63 | -3.63 | 13.17 | 1.5 |
| 1130 | 1135.85 | -5.85 | 34.26 | 4.95 |
| 1117 | 1123.08 | -6.08 | 36.94 | 0.05 |
| 1106 | 1110.3 | -4.3 | 18.51 | 3.15 |
| 1368.3 | 2313.41 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 1,001 , т.е. (d2 Пример . По данным за 24 месяца построено уравнение регрессии зависимости прибыли сельскохозяйственной организации от производительности труда (x1): y = 300 + 5x .
Получены следующие промежуточные результаты:
∑ε 2 = 18500
∑(εt— εt-1) 2 = 41500
Рассчитайте критерий Дарбина-Уотсона (при n=24 и k=1 (число факторов) нижнее значение d = 1,27, верхнее d = 1,45. Сделайте выводы.
Решение.
DW = 41500/18500 = 2,24
d2 = 4- 1,45 =2,55
Поскольку DW > 2,55, то следовательно, имеются основания считать, что автокорреляция отсутствует. Это является одним из подтверждений высокого качества полученного уравнения регрессии y = 300 + 5x .
Видео:Автокорреляция остатков. Критерий Дарбина-УотсонаСкачать

20. Автокорреляция в остатках. Критерий Дарбина-Уотсона
Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего эти остатки могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени T.
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.
Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:

Т. е. величина D есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Можно показать, что при больших значениях N существует следующее соотношение между критерием Дарбина-Уотсона D и коэффициентом автокорреляции остатков первого порядка 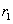
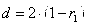
Таким образом, если в остатках существует полная положительная автокорреляция и 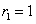
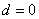
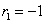
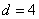
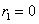
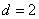
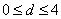
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза 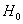
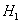
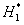
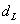
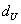
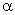
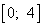
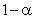
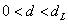
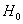
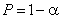
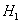
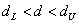
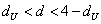
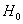
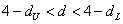
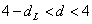
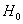
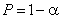
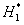
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу 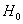
Пример. Проверим гипотезу о наличии автокорреляции в остатках для аддитивной модели нашего временного ряда. Исходные данные и промежуточные расчеты заносим в таблицу:
🌟 Видео
Excel для полных чайников Урок 16 Линия трендаСкачать
Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Коэффициент корреляции. Статистическая значимостьСкачать

Проверка гипотезы о распределении случайной величины. Критерий хи-квадрат Пирсона.Скачать

Решение задач в Microsoft Excel. Линии трендаСкачать

Уроки Excel. Статистические функции. Линия Тренда.Скачать

10-09 Критерий КолмогороваСкачать

Где конец ТРЕНДА? Как определить окончание ТРЕНДА на КРИПТОРЫНКЕ? Обучение трейдингу!Скачать

Как безошибочно определять РАЗВОРОТ ТРЕНДА Индикатор кумулятивная дельта. Cumulative DeltaСкачать

Самый простой метод определения Тренда.Скачать

КАК УЗНАТЬ О РАЗВОРОТЕ ТРЕНДА? ДИВЕРГЕНЦИЯ - ЧТО ЭТО?Скачать

Видео-лекция к практическому заданию "Корреляционно-регрессионная модель в MS Excel"Скачать

Прогнозирование в Excel при помощи функции "ПРЕДСКАЗ" основании таблиц аналитики.Скачать

10-10 Критерий ПирсонаСкачать

10-11 Критерий Колмогорова в pythonСкачать

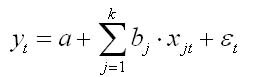
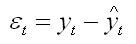
.jpg)