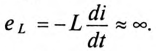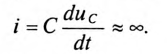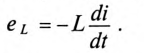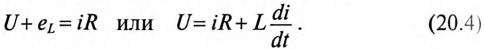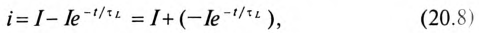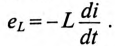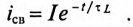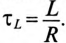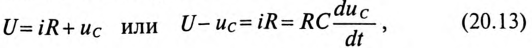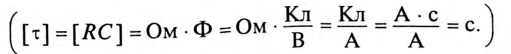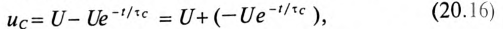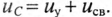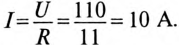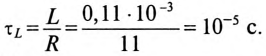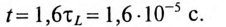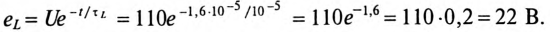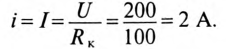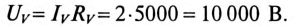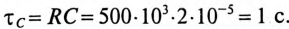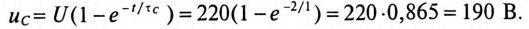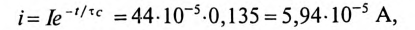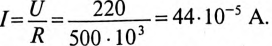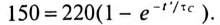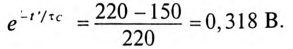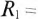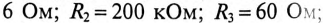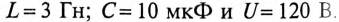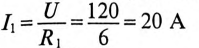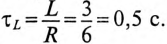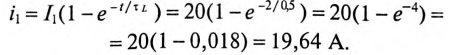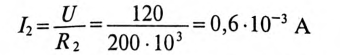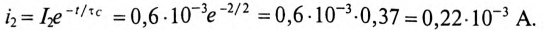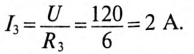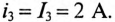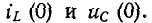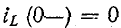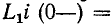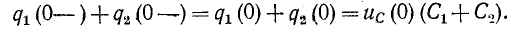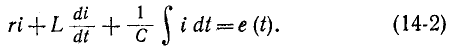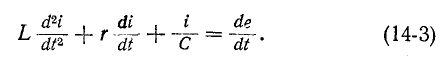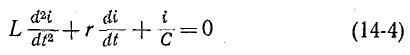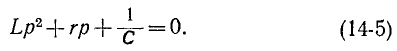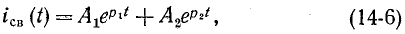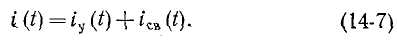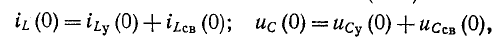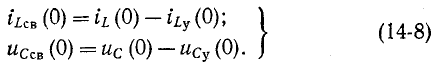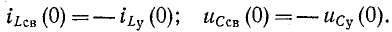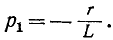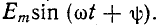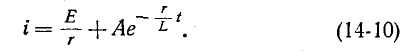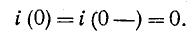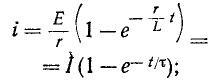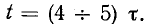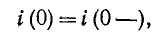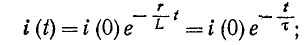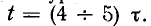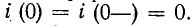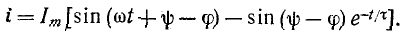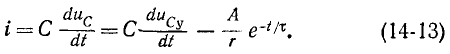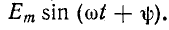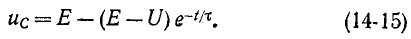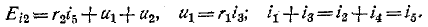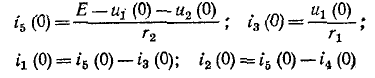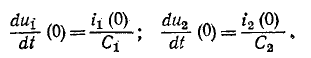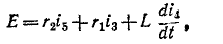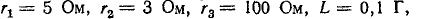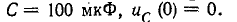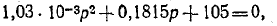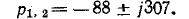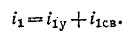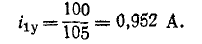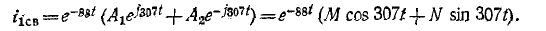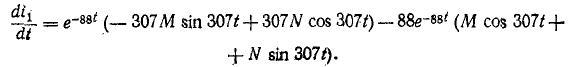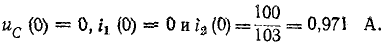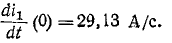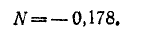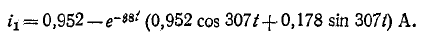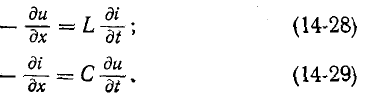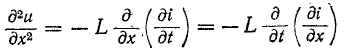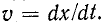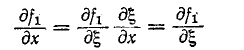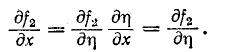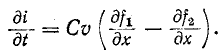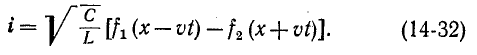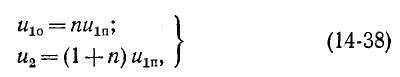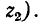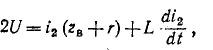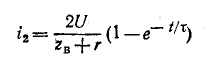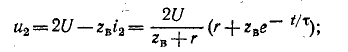При проектировании технической системы в качестве критериев ее оптимальности принимают показатели эффективности и качества процессов функционирования. Функционирование технической системы происходит в условиях внешней среды. Любое изменение внешних возмущающих или управляющих воздействий приводит к возникновению переходного процесса. В переходном процессе могут возникать большие амплитуды отклонений фазовых координат, сопровождающиеся значительным повышением деформаций и напряжений в конструктивных элементах технической системы.
Отклонения фазовых координат от оптимальных значений отрицательно влияют на выполнение технологического процесса, снижая качество продукции. Периодические внешние воздействия возбуждают вибрации, оказывающие вредное воздействие на организм человека и сокращающие срок службы механизмов технической системы.
При изменении внешнего воздействия u <t)любая фазовая координата технической системы v(t) может быть представлена состоящей из двух составляющих
где vB(t) — вынужденная установившаяся составляющая, определяемая частным решением неоднородного дифференциального уравнения, описывающего функционирование технической системы; ип(?) — переходная составляющая, характеризующая свободный переходный процесс и определяемая общим решением однородного дифференциального уравнения (без правой части).
Если техническая система устойчива, переходная составляющая с течением времени затухает и остается лишь вынужденная составляющая. О качестве переходных процессов имеет смысл говорить лишь для устойчивой системы. Абсолютное большинство создаваемых технических объектов должно обладать устойчивостью режимов их функционирования, что вытекает из требований, обусловленных их назначением. Если в процессе проектирования такого объекта какой-либо вариант его структуры или совокупность параметров не обеспечивает устойчивости, он должен быть исключен из дальнейшего рассмотрения по причине принципиальной непригодности. Однако встречаются объекты, в которых неустойчивость в некоторой области фазового пространства оказывается весьма полезной и используется в практических целях (например, в механизмах опрокидывания кузовов транспортных средств, кантователях, механизмах для забивки свай и др.).
Устойчивая техническая система может работать в установившемся или неустановившемся режиме. Поэтому возникает необходимость оценки качества процессов, описываемых обеими составляющими vn(t) и ив(?). Различают две группы показателей: первую составляют показатели качества переходного процесса, а вторую — показатели, характеризующие вынужденную составляющую, по которой определяется точность выполнения алгоритма функционирования в установившемся режиме.
Сравнительная оценка динамических свойств различных технических систем возможна лишь при одинаковых условиях их функционирования. Поэтому при моделировании используют различные тестовые воздействия на систему. При анализе переходных процессов применяют следующие виды воздействий: ступенчатое, импульсное, кусочно-линейное, экспоненциальное, гармоническое. Установившиеся процессы изучают при гармонических внешних воздействиях или случайных воздействиях, описываемых стационарными случайными функциями с заданными статистическими характери-
Поскольку данная глава посвящена анализу переходных процессов, перейдем непосредственно к изложению вопросов оценки показателей качества этих процессов. Наиболее часто при моделировании технических систем качество переходных процессов оценивают по графику переходной характеристики.
Переходной характеристикой называют реакцию технической системы на ступенчатое воздействие. Переходную характеристику в теории автоматического управления рекомендуют получать при нулевых начальных условиях Uj0 = 0, i)i0 = 0, i = 1,/г, и единичном ступенчатом воздействии:
Однако эти рекомендации могут оказаться неприемлемыми для сложных технических систем. Это прежде всего обусловлено нелинейностью их характеристик, а также сложной (разветвленной, кольцевой и т.д.) структурой и многомерностью. Возникает необходимость приближения уровней изменения внешних воздействий и их характеристик к реальным, обусловленным характерными условиями эксплуатации. Поэтому переходные процессы таких систем исследуют при ступенчатых воздействиях вида
где и0 и ик — начальное и конечное значения функции воздействия u(t), причем Uq = const И UK = const, U^^Uq.
Переходную характеристику vn(t) определяют посредством численного интегрирования системы дифференциальных уравнений, описывающих функционирование технического объекта. Переходная характеристика vn(t) представляет собой график, отображающий процесс изменения во времени некоторой фазовой координаты vt технической системы при переходе ее из одного установившегося статического состояния в другое. Поэтому для получения переходной характеристики в процессе вычислительного эксперимента и последующей оценки показателей качества переходного процесса необходимо предварительно определить начальные и конечные значения всех фазовых координат технической системы в начальном и конечном равновесных статических состояниях. Эти состояния могут быть двух видов: состояние покоя или состояние равномерного движения элементов технической системы. Так, например, для механических систем обычно рассматривают состояние покоя, для гидравлических — состояние равномерного движения жидкости в магистрали, для тепловых — состояние установившейся теплопередачи.
В случае состояния покоя определяют значения фазовых координат системы yj0Hi;iK,i=l,ra, при vi0— viK = 0. Если равновесным состоянием принимают равномерное движение, то определяют значения i)i0 = 1,тг, при условии
vi0 = const; viK — const. Начальные и конечные значения фазовых переменных определяют на основе использования численных методов анализа статических состояний, изложенных в главе 8.
Для оценки качества переходного процесса используют следующие показатели:
- ? время переходного процесса tu, характеризующее длительность пребывания технической системы в неустановившемся состоянии (динамическом режиме);
- ? коэффициент динамичности kR, характеризующий максимальное отклонение фазовой координаты от ее значения в установившемся конечном состоянии vK;
- ? декремент колебаний D, характеризующий скорость затухания колебаний в технической системе;
- ? колебательность К, определяющую число колебаний за время tn;
- ? интегральные оценки I, характеризующие отклонение графика переходного процесса от идеальной или эталонной характеристики.
Длительность переходного режима даже при быстром затухании динамического процесса теоретически бесконечна, поэтому на практике считают переходный процесс завершенным, если значение фазовой переменной v(t) перестает отличаться от установившегося конечного значения не более чем на определенную величину. Условие завершения переходного процесса принимают в виде
где Voo — значение фазовой координаты и при t —> т.е. в конечном установившемся состоянии технической системы: Voo=vK; А — величина, определяющая область изменения v(t), в которой можно пренебречь различием между v(t)HVoo.
Величину А назовем коридором стабилизации установившегося состояния. Значение А принимают согласно выражению
Коэффициент ? характеризует ширину коридора стабилизации установившегося состояния. Обычно принимают ? = 0,05. Это означает, что при t > tn значение v(t) отличается от Av не более чем на 5 %.
Время переходного процесса^ определяют по графику переходной характеристики v(t) (рис. 9.12, а и б). Оно равно интервалу времени, измеряемому от момента времени t —10, при котором осуществляется скачок сигнала воздействия на техническую систему u(t) (подача ступенчатого сигнала), до момента, соответствующего последнему пересечению переходной характеристикой линий коридора стабилизации установившегося состояния.
Время переходного процесса характеризует быстродействие технической системы. Чем меньше значение ?п, тем быстрее наступает стабилизация характеристик работы системы при изменении ее режима, обусловленного управляющими или возмущающими воздействиями. Особенно важно высокое быстродействие для систем автоматического управления.
Рис. 9.12. К определению показателей качества переходных процессов: а — при колебательных процессах; б — при апериодических процессах
Коэффициент динамичности определяют по формуле
где Атах — максимальная амплитуда отклонения фазовой координаты v от конечного установившегося ее значения v
v3i — i-e экстремальное значение фазовой координаты, определяемое из условия dv/dt = 0.
Если величина Av значительно меньше| Voo , то вместо Av в формулах (9.104) и (9.106) рекомендуется принять | Ноо |.
Значение ka показывает, во сколько раз максимальное динамическое отклонение фазовой координаты в переходном процессе превышает статическое отклонение Av при переходе технической системы из одного стационарного состояния в другое. Чем выше значение kR, тем больше отклонение характеристик работы технической системы от оптимальных и тем хуже ее динамические свойства. При высоких требованиях к характеристикам функционирования технической системы величина &д не должна превышать 1,2. 1,24. Такие значения характерны для некоторых систем автоматического управления. В большинстве же случаев при проектировании технических объектов принимают допустимые значения &д в пределах 1,25. 1,45.
Декремент колебаний определяют по формуле
где А1 иА2 — амплитуды двух смежных отклонений фазовой координаты от значения Voo’, u3i и и э2 — смежные экстремальные значения переходной характеристики.
Чем выше значение D, тем быстрее затухают колебания.
Колебательность К определяется числом амплитудных значений v3i за время tu (или числом полупериодов колебаний). При высоких требованиях к переходным процессам К не должно превышать 1. 2, а при умеренных 3. 5.
В технических системах с апериодическими переходными процессами (рис. 9.12, б) фазовые координаты vt не достигают экстремальных значений, поэтому йд = 1, а в связи с отсутствием колебаний D и К не оцениваются. Динамичность апериодических переходных процессов минимальная. Однако для многих физических систем такие процессы практически недостижимы. Кроме того, часто длительность апериодических процессов оказывается недопустимо большой.
Интегральные оценки позволяют обобщенно оценить быстродействие технической системы и отклонение ее фазовых координат от установившихся значений в переходных процессах. При этом используют интегралы вида
Интеграл численно равен площади, ограниченной осью ординат, графиком v(t) и линией щ, (заштрихованная площадь на рис. 9.13, а). Иногда вместо (9.109) используют выражение, определяющее относительную площадь:
Интеграл /3 определяет степень отклонения переходной характеристики v(t)oT идеальной переходной характеристики АВС при ступенчатом внешнем воздействии (рис. 9.13, а).
Интегральные оценки также используют для определения степени соответствия получаемой переходной характеристики v(t) заданной эталонной характеристике v3 (t):
В этом случае интеграл /4 равен площади, ограниченной графиками v(t) и v3 (t) (заштрихованная площаь на рис. 9.13, б). Интегралы /2 и /5 используют для оценки колебательных переходных процессов.
При проектировании технических систем интегральные оценки подлежат минимизации.
Рис. 9.13. К определению интегральных показателей качества переходных процессов: а — по формуле (9.109); б — по формуле (9.112)
- №74 Расчет переходных процессов методом переменных состояния.
- Оценка качества процессов регулирования
- Оценка качества процессов регулирования
- Переходные процессы в электрических цепях
- Переходный процесс в электрической цепи
- Подключение катушки индуктивности к источнику с постоянным напряжением
- Отключение и замыкание RL-цепи
- Зарядка, разрядка и саморазрядка конденсатора
- Переходные процессы в электрических цепях. Классический метод расчета
- Законы коммутации и начальные условия
- Установившийся и свободный режимы
- Переходный процесс в цепи r, L
- Переходный процесс в цепи r, С
- Включение в цепь r, С постоянной э. д. с.
- Переходные процессы в цепях с распределенными параметрами
- 🎥 Видео
Видео:c07 6, Показатели качества управления: прямые показатели качестваСкачать

№74 Расчет переходных процессов методом переменных состояния.
Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.
В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:
Та же система уравнений в матричной форме:
или в обобщённой матричной форме:
Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:
Значения производных на к-ом шаге:
Значения переменных на к-ом шаге:
Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).
Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].
Последовательность расчета переходного процесса методом переменных состояния выглядит так:
1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.
3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.
4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.
5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.
Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).
1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа:
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.
Для этой цели из (1) выражаем
и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:
Подсчитаем значения отднльных коэфициэнтов:
Составляем матрицы коэффициентов:
В качества исследуемого промежутка времени выбираем период переменного тока
Число шагов интегрирования принимаем N = 1000,
Вводим исходные данные в ЭВМ и выполняем рассчет.
В качестве выходной функции принимаем:
Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Оценка качества процессов регулирования
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Оценка качества процессов регулирования
Система может быть устойчивой, т. е. ее переходный процесс носит затухающий характер, но время затухания настолько велико или ошибка в установившемся режиме настолько большая, что практически данная система не может быть использована. Поэтому система должна быть не только устойчивой, но и иметь определенный переходный процесс, а ее ошибки в установившихся режимах не должны превышать допустимых.
Для сравнительного анализа различных автоматических систем необходимо иметь некоторые числовые характеристики этих систем, позволяющие оценивать, какая из них будет более эффективной. Эти числовые характеристики и называются критериями качества.
Критерии качества позволяют дать количественную оценку различным автоматическим системам и тем самым обоснованно подойти к выбору системы и ее закона управления, удовлетворяющему выбранному критерию качества.
Комплекс требований, определяющих поведение автоматической системы в установившихся и переходных процессах отработки заданного воздействия, определяется понятием «качество процесса регулирования» или «качество автоматической системы».
Автоматическая система называется качественной, если она удовлетворяет определенным технологическим требованиям: например, как будет меняться реакция автоматической системы, если на ее вход действуют различного рода возмущения как по каналу управления, так по каналу возмущения, т. е. обеспечивается ли принципиальная возможность прихода автоматической системы в некоторое установившееся состояние. Такое понятие качества автоматической системы охватывает ее статические и динамические свойства, выраженные в количественной форме и получившие название показателей качества автоматического регулирования.
Учитывая большое разнообразие автоматических систем и объектов регулирования, в настоящее время разработано большое число различных критериев, которые, с одной стороны, включают взаимоисключающие требования, а с другой — между показателями качества существует тесная взаимосвязь, поэтому стремление улучшить какой-либо из них может привести к ухудшению другого. Так, например, стремление уменьшить ошибку автоматического регулирования приводит к уменьшению запаса устойчивости и быстродействия и наоборот, или повышение надежности автоматической системы неизбежно приводит к увеличению ее стоимости.
Мы уже знаем, что автоматическая система прежде всего должна быть устойчивой, однако это необходимое, но недостаточное условие для эффективной работы автоматической системы. В устойчивой системе переходный процесс затухает. Однако для практики вовсе не безразличен характер затухания переходного процесса. Так, например, если переходный процесс затухает медленно, и система долго входит в новый установившийся режим, то она обладает недостаточным быстродействием, и, следовательно, ее применение будет ограничено. Поэтому устойчивость является необходимым, но недостаточным условием работоспособности автоматических систем. Достаточным условием является качество процессов регулирования, которое оценивается качеством переходных процессов и ошибками в установившихся режимах.
Оценки качества работы автоматических систем, полученные непосредственно по кривым переходного процесса, называют прямыми. Вычисление всех этих критериев основывается на использовании математического аппарата управления, причем наиболее часто при вычислении критериев качества используются временные и частотные характеристики автоматических систем. Анализ переходных процессов сводится к отысканию общего решения неоднородного дифференциального уравнения, описывающего физические процессы в автоматической системе при заданных начальных условиях и известных внешних воздействиях, а также к анализу влияния изменения параметров автоматической системы на вид этого решения. Следует отметить, что аналитическое решение уравнений требует вычисления корней характеристического уравнения и вычисления постоянных интегрирования, что для уравнений выше третьего порядка невозможно.
Поэтому применяют приближенные методы анализа переходных процессов, не требующие, так же как и при исследовании устойчивости автоматических систем, непосредственного решения дифференциальных уравнений. Чаще всего при анализе качества работы автоматических систем требуется лишь установить, находится ли переходный процесс внутри области допустимых значений регулируемой величины или выходит за ее пределы. Оценки, получаемые этим методом, называют косвенными.
Прямые показатели качества переходных процессов. Качество переходных процессов обычно оценивают по переходной функции, которая представляет собой реакцию автоматической системы на внешнее воздействие типа единичного скачка. На примере переходной функции познакомимся с основными показателями качества переходного процесса:
1. Ошибка регулирования;
2. Время регулирования;
3. Перерегулирование;
4. Степень колебательности;
5. Количество колебаний.
Использование того или иного показателя работы автоматической системы или их комбинации в виде критериев качества определяется удобством его применения в системах автоматического регулирования, а также, в известной мере, сложившимися традициями.
Ошибка регулирования равна разности между требуемым и действительным значениями регулируемой величины e (t) = x (t) — y (t). Знание мгновенного значения ошибки в течение всего времени работы объекта регулирования позволяет наиболее полно судить о свойствах автоматической системы. Однако в действительности, вследствие случайности задающего и возмущающего воздействий, такой подход не может быть реализован. В практике анализа автоматических систем используется метод исследования в различных типовых режимах.

Для статических автоматических систем определяется абсолютное e и относительное d значения ошибки регулирования. Относительное значение ошибки регулирования можно вычислить по выражению
Для астатических автоматических систем пользуются правилом, которое позволяет установить, устраняет ли астатический регулятор статическую ошибку от какого-либо либо возмущения. Для выполнения этого необходимо, чтобы интегрирующее звено было включено в цепь регулирования до места приложения данного возмущения. Это объясняет тот факт, что включение интегрирующих элементов и повышение степени астатизма не дает возможности устранить ошибку чувствительного элемента, которую можно рассматривать как возмущение.


Возмущающее воздействие принимается постоянным. Этот режим практически используется только в следящих системах и системах программного регулирования.

В зависимости от конкретного вида автоматической системы возмущающие воздействия в рассматриваемом режиме могут оставаться постоянными или изменяться во времени.
Во всех режимах в зависимости от постоянства или изменения возмущающих воздействий появляется некоторая абсолютная e (t) или относительная d (t) постоянная ошибка. Более вероятным является случай, когда возмущающие воздействия при движении автоматической системы в этом режиме меняются во времени. то объясняется тем, что при движении по гармоническому закону непрерывно будет меняться направление движения автоматической системы, а следовательно, одновременно будет меняться напрявление действующих в автоматической системе сил сухого трения. Этот случай является довольно сложным, и он может рассматриваться только в приложении к конкретным автоматическим системам.
Время регулирования tp определяется длительностью переходного процесса. Теоретически переходный процесс длится бесконечно долго, однако практически считают, что он заканчивается, как только отклонение регулируемой величины от нового ее установившегося значения не будут превышать допустимых пределов |у (t) — ууст |
Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Переходные процессы в электрических цепях
Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 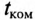
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 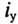
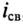
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Видео:Теория автоматического управления. Лекция 13. Прямые показатели качества регулированияСкачать

Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
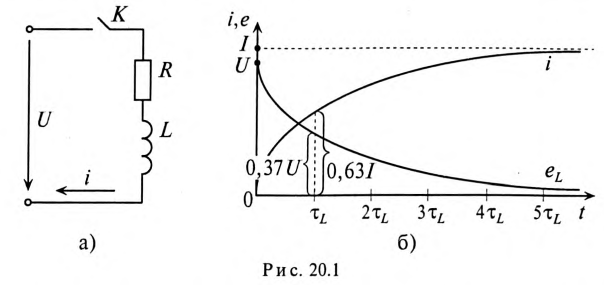
Подключение катушки индуктивности к источнику с постоянным напряжением
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 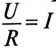
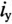
Отношение — 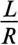
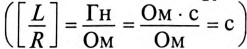
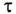
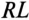
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (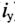
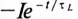
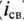
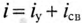
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t= 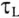
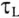
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 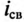
Таким образом, ЭДС самоиндукции в 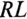
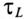
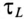
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
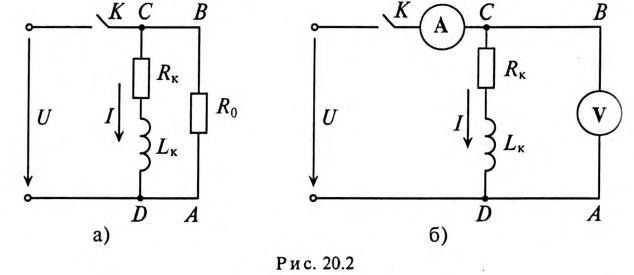
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 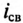
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 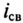
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 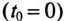
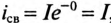
Для определения активного сопротивления катушки 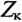
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
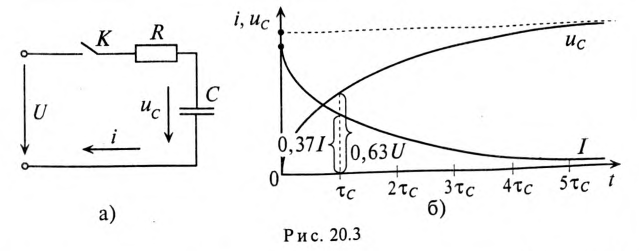
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 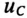
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 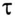
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 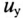
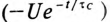
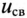
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
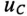

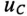
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 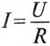
За время t= 

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 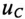
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 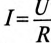

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 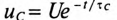
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 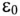
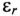
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 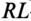
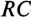
Пример 20.1
Катушка электромагнита с параметрами 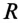
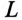
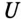
Решение
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
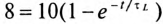
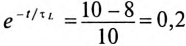
По Приложению 9 определяется 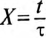
ЭДС самоиндукции за время 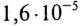
Пример 20.2
К зажимам катушки индуктивности с параметрами 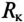
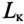
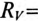
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 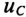
Решение
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
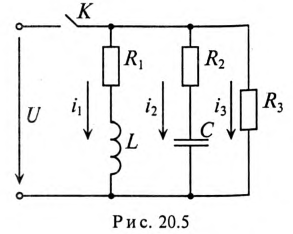
Пример 20.4
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 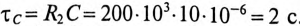
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 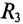
Постоянная времени 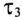
Через 2 с значение тока будет таким же, т. е.
Видео:Лекция 091-5. Расчет переходных процессов классическим методом. Корни характеристического уравненияСкачать

Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 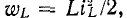
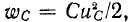
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 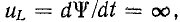
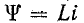
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток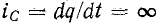
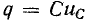
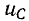
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через 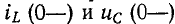
На основании законов коммутации: 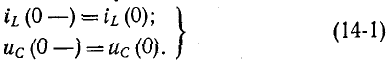
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца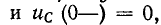
В случае ненулевых начальных условий, т. е. когда 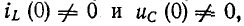
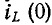
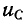
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
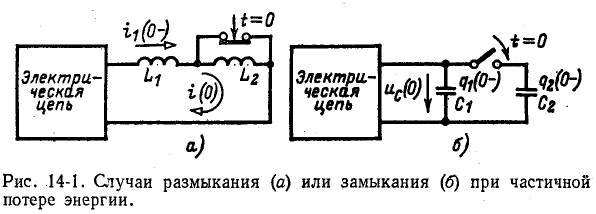
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 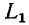
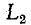
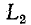
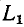
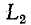
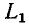
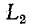
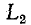
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 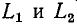
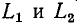
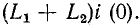
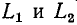
Найденный таким образом ток 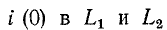
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 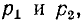
где 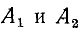
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия 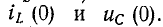
откуда
Итак, начальные значения свободных функций 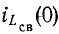
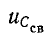
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
Переходный процесс в цепи r, L
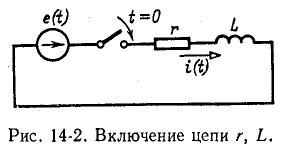
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени 
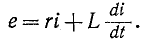
Характеристическое уравнение имеет вид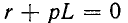
Отсюда свободный ток
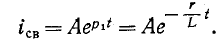
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
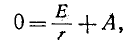
откуда 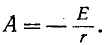
здесь 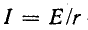
В начальный момент t = 0 э. д. с. самоиндукции 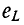
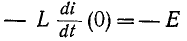
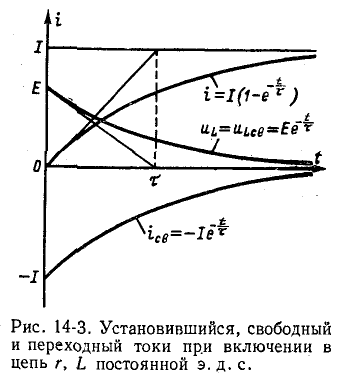
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности 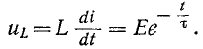
Из курса математического анализа известно, что если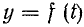
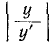
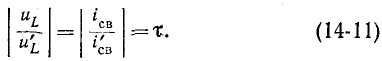
Величина 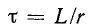
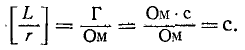
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой 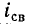
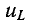
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
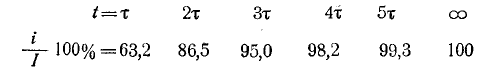
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы», переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
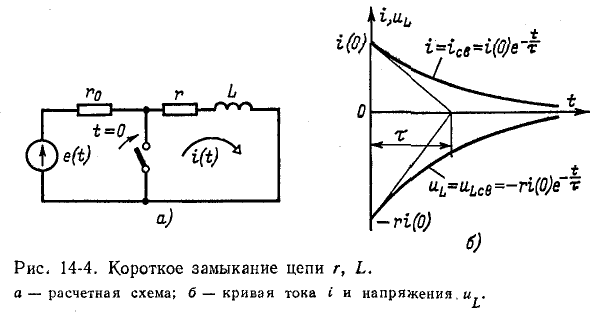
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9) 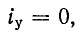
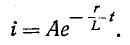
Постоянная интегрирования А находится из начального условия
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 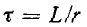
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 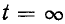
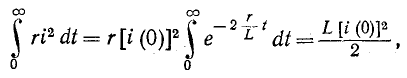
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
3. Включение в цепь r, L синусоидальной э. д. с.
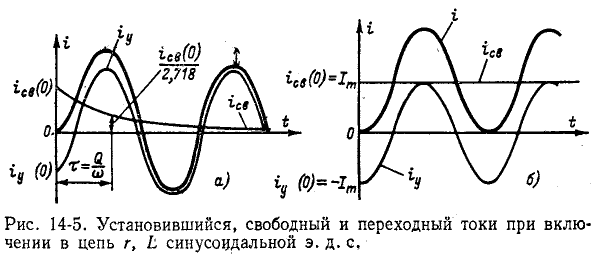
При включении в цепь r, L синусоидальной э. д. с. 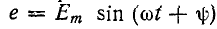
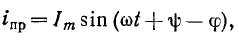
где 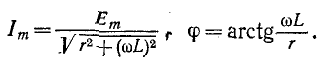
На основании (14-9) 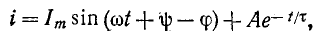
где 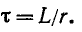
Постоянная интегрирования определяется по начальному условию
Следовательно, 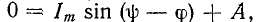
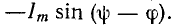
На рис. 14-5, а изображены кривые 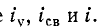
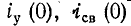
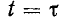
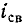
контура Q и обратно пропорциональна частоте 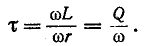
Если в момент коммутации (t = 0) ток 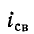
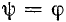
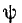
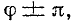
Если же коммутация происходит при 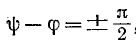
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 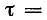
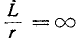
При достаточно большой постоянной времени 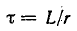
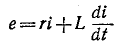
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно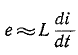
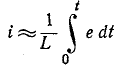
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
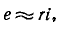
откуда
.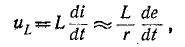
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t 
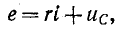
где 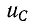
С учетом того, что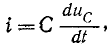
получим:
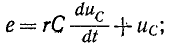
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение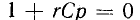
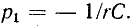
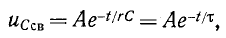
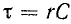
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем 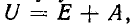
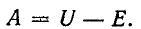
Согласно (14-13) ток в контуре
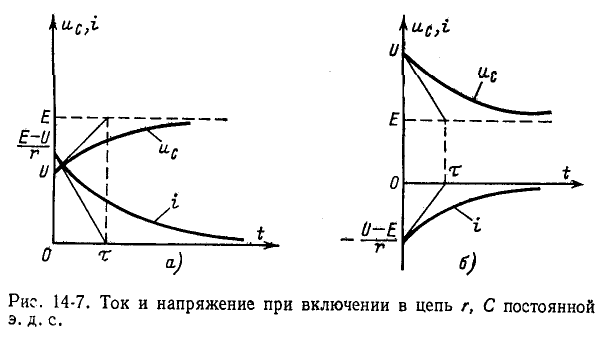
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 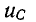
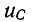
Если Е 0), убывающей (с 0) или убывающей (с 1 В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 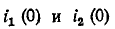
Подстановка в эти уравнения найденных значений 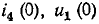
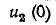
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
откуда при t = О
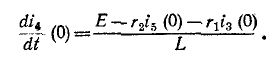
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
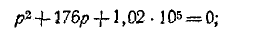
корни характеристического уравнения комплексные:
В начальный момент 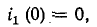
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви 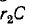
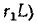
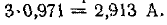
производной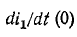
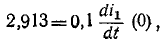
Следовательно, подставляя значение 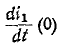
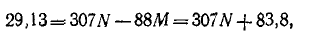
откуда
Итак,
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных: 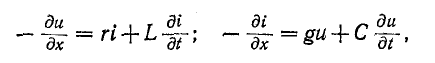
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
Дифференцируя (14-28) по х:
и используя (14-29), получаем: 
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко—лебаний струны. Его решение дано Даламбером и имеет вид: 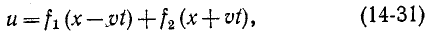
где 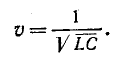
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 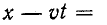
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 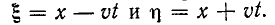
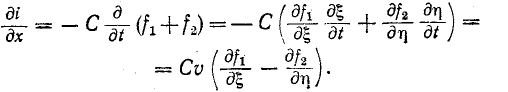
Но
Интегрирование последнего уравнения дает 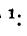
Выражения (14-31) и (14-32) записываются сокращенно:
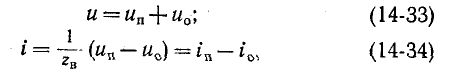
здесь 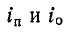
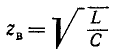
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом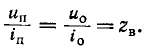
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 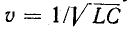
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 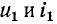
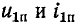
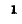
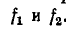
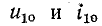
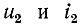
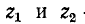
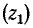
В месте неоднородности выполняется условие равенства
напряжений и токов: 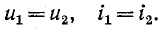
Следовательно, 
Подстановка в (14-36) значений 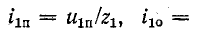
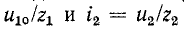
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 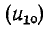
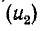
где 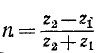
Соответственно ток отраженной волны
а ток преломленной волны
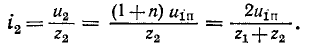
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 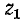
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
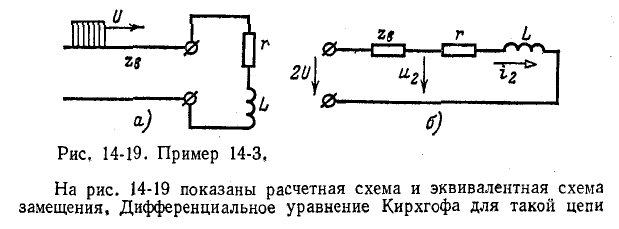
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 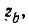
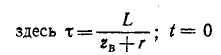
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
Лекция 122. Переходные процессыСкачать

Метод переменных состояния │ПЕРЕХОДНЫЕ ПРОЦЕССЫ. ПримерСкачать

Расчет переходных процессов классическим методомСкачать

Расчёт переходных процессов операторным методомСкачать

Лекция 091-1. Физические основы переходных процессовСкачать

Основы электротехники. 06. Переходные процессыСкачать

Расчёт переходных процессов методом переменных состоянияСкачать

Лекция 091-3. Расчет переходных процессов. Принужденные и свободные составляющиеСкачать

Предельные вероятности состоянийСкачать

Расчёт переходного процесса при коммутации на стыке двух линийСкачать

Расчет переходного процесса в цепи второго порядка.Скачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Васильева О. Н. - Электромагнетизм. Семинары - Переходные процессы в электрических цепяхСкачать