Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Нахождение геометрических мест точек
- 1.1. Найти множество точек, отношение расстояний которых до двух данных перпендикулярных прямых постоянно и равно X.
- 1.2 Найти множество точек, сумма квадратов расстояний которых до двух данных точек постоянна и равна а 2 .
- 1.3. Найти множество точек, для каждой из которых отношение квадрата расстояния до данной точки к расстоянию до данной прямой, не проходящей через эту точку, постоянно и равно а.
- 1.4. Найти множество середин отрезков, соединяющих данную точку с точками:
- а) данной прямой;
- б) данной окружности;
- в) данной параболы;
- г) данного отрезка.
- 1.5. Найти множество концов В отрезков АВ, исходящих из данной точки А, если известно, что их середины лежат:
- а) на данной прямой;
- б) на данной окружности;
- в) на данной гиперболе.
Указание. Рассмотреть два различных положения отрезка, PQ и Р, Q1, и установить, что PQ || PjQj.
1.75. Найти ГМТ, сумма расстояний которых от двух данных параллельных прямых есть величина постоянная, равная данному отрезку d.
Указание. Допустив, что задача решена, найти расстояние какой- либо точки искомого ГМТ до одной из данных параллельных прямых.
1.76. Найти ГМТ, сумма расстояний которых от двух данных параллельных прямых больше данного отрезка d.
Указание. См. предыдущую задачу. Искомым ГМТ будут две полуплоскости.
1.77. Дан отрезок АВ = а. Найти ГМТ, отстоящих от АВ на расстоянии, меньшем данного отрезка d, и из которых АВ виден под углом, большим данного угла а.
Указание. Искомое ГМТ есть пересечение (общая часть, рис. П.1) двух фигур Ф: и Ф2. Контур AKAlA2LBA3A4 общей части этих фигур не принадлежит искомому ГМТ.
1.78. Найти ГМТ середин отрезка АВ, концы которого скользят по сторонам данного прямого угла.
Указание. Воспользоваться свойством медианы, проведенной из вершины прямого угла.
- 1.79. Дан квадрат. Найти ГМТ точек М, таких что расстояние от М до центра квадрата не превосходит расстояния от М до любой вершины квадрата.
- 1.80. Найти ГМТ, из которых данный квадрат виден под углом 60°.
- 1.81. Даны окружность и точка Л. Найти геометрическое место середин всевозможных хорд, таких, что прямая, которой эта хорда принадлежит, проходит через точку А.
- 1.82. Дана прямая I и две точки А и В по одну сторону от нее. Найти геометрическое место центров всевозможных окружностей, проходящих через А и В и пересекающих прямую I.
- 1.83. Найти геометрическое место точек М, таких что АМ 2 +ВМ 2 =СМ 2 , где А, В, С — данные точки плоскости.
- 1.84. ABCD — трапеция. Найти геометрическое место точек М, таких что AM 2 + СМ 2 = ВМ 2 + DM 2 .
- 1.85. На окружности фиксированы точки А и В, а точка С перемещается по окружности. Найти геометрическое место точек пересечения: а) медиан; б) высот; в) биссектрис треугольников АВС.
- 1.86. Найти геометрическое место середин всевозможных отрезков с концами на противоположных сторонах данного четырехугольника.
- 1.87. Через точку М, расположенную внутри параллелограмма, проведены две прямые, параллельные его сторонам. Найти геометрическое место точек М, если:
- а) два параллелограмма из четырех получившихся, не имеющие общей стороны, равновелики;
- б) сумма площадей двух параллелограммов равна сумме площадей двух других.
- 1.88. Найти геометрическое место точек, для которых: а) сумма; б) разность расстояний до двух заданных прямых равна заданной величине.
- 1.89. Около данной окружности описан треугольник АВС, у которого ZA > ZB> ZC. Найти геометрическое место вершин А, В, С.
- 1.90. Найти геометрическое место таких точек М внутри данного треугольника, которые являются серединами не менее чем двух различных отрезков с концами на сторонах этого треугольника.
- 1.91. Даны точки А и В. Найти геометрическое место точек С, таких что в треугольнике АВС медиана AM равна высоте BN.
- 1.92. Даны окружность и точка А. Произвольная окружность, проходящая через А, пересекается с данной в точках В и С. Касательная к этой окружности в точке А пересекается с прямой ВС в точке М. Найти геометрическое место точек М.
- 1.93. Через точку пересечения двух окружностей проведена прямая, вторично пересекающая окружности в двух точках А и В. Найти геометрическое место середин отрезков АВ.
- 1.94. Даны точка А и прямая I, В — произвольная точка на I. Найти геометрическое место точек М, таких что АВМ — правильный треугольник.
- 1.95. Дан правильный треугольник АВС. На продолжении его сторон АВ и АС за точки В и С взяты точки D и Е так, что BD ? СЕ = ВС 2 . Найти геометрическое место точек пересечения прямых DC и BE.
- 1.96. Даны три точки А, В, и С на прямой, D — произвольная точка плоскости, не лежащая на этой прямой. Проведем через С прямые, параллельные AD и BD, до пересечения с прямыми BD и AD в точках Р и Q. Найти геометрическое место оснований М перпендикуляров, опущенных из С на PQ, а также найти все точки D, для которых М — фиксированная точка.
- 1.97. На стороне АС треугольника АВС взята точка К, а на медиане BD — точка Р так, что площадь треугольника АРК равна площади треугольника ВРС. Найти геометрическое место точек пересечения прямых АРиВК.
- 1.98. В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Пусть Р — произвольная точка окружности, РА пересекает BD в точке Е. Прямая, проходящая через Е параллельно АС, пересекается с прямой РВ в точке М. Найти геометрическое место точек М.
- 1.99. Даны угол, вершина которого в точке А, и точка В. Произвольная окружность, проходящая через А и В, пересекает стороны угла в точках С и D (отличных от А). Найти геометрическое место центров тяжести треугольников ACD.
- 1.100. Одна вершина прямоугольника находится в данной точке, две другие, не принадлежащие одной стороне, — на двух заданных взаимно перпендикулярных прямых. Найти геометрическое место четвертых вершин таких прямоугольников.
- 1.101. Пусть А — одна из двух точек пересечения двух данных окружностей; через другую точку пересечения проведена произвольная прямая, пересекающая одну окружность в точке В, а другую — в точке С, отличных от общих точек этих окружностей. Найти геометрическое место:
- а) центров окружностей, описанных около АВС;
- б) центров тяжестей треугольников АВС;
- в) точек пересечения высот треугольников АВС.
- 1.102. Пусть В и С — две фиксированные точки данной окружности, А — переменная точка этой же окружности. Найти геометрическое место оснований перпендикуляров, опущенных из середины АВ на АС.
- 1.103. Найти геометрическое место точек пересечения диагоналей прямоугольников, стороны которых (или их продолжения) проходят через четыре данные точки плоскости.
- 1.104. Через точку, лежащую на равном расстоянии от двух данных параллельных прямых, проведена прямая, пересекающая эти прямые в точках М и JV. Найти геометрическое место вершин Р равносторонних треугольников MNP.
- 1.105. Точки А, В и С расположены на одной прямой (В — междуА и С). Найти геометрическое место точек, таких что ctgZAMB + ctgZBMC = к (fc = const).
- 1.106. Даны две точки А и Q. Найти геометрическое место точек В, таких что существует остроугольный треугольник АВС, для которого Q — точка пересечения медиан.
- 1.107. Даны угол и окружность с центром в точке О, вписанная в этот угол. Произвольная прямая касается окружности и пересекает стороны угла в точках М и N. Найти геометрическое место центров окружностей, описанных около треугольников MON.
- 1.108. Даны две окружности, на них взяты по одной точке А и В, равноудаленные от середины отрезка, соединяющего их центры. Найти геометрическое место середин отрезков АВ.
- 1.109. Дан отрезок АВ. Возьмем на АВ произвольную точку М и рассмотрим два квадрата AMCD и MBEF, расположенные по одну сторону от АВ. Опишем около этих квадратов окружности и обозначим через N их точку пересечения, отличную от М. Доказать, что: a) AF и ВС пересекаются в N; б) MN проходит через фиксированную точку плоскости. Найти геометрическое место середин отрезков, соединяющих центры квадратов.
- 1.110. Даны окружность и точка А. Пусть М — произвольная точка окружности. Найти геометрическое место точек пересечения серединного перпендикуляра к отрезку AM и касательной к окружности, проходящей через М.
- 1.111. Две окружности касаются друг друга в точке А. Одна прямая, проходящая через А, пересекает вторично эти окружности в точках В и С, другая — в точках Ва и Сг (В и Вг — на одной окружности). Найти геометрическое место точек пересечения окружностей, описанных около треугольников АВУС и АВСг.
- 1.112. Найти геометрическое место вершин прямых углов всевозможных равнобедренных прямоугольных треугольников, концы гипотенуз которых лежат на двух заданных окружностях.
- 1.113. Прямоугольный треугольник ABC (ZC = 90°) перемещается по плоскости таким образом, что вершины его А и В скользят по сторонам данного прямого угла О. Доказать, что вершина С опишет отрезок.
Указание. Описать вокруг АВСО окружность и рассмотреть углы ВАС и ВОС, заметив при этом, что угол ВАС постоянный.
1.114. Найти ГМТ плоскости, из которых данный отрезок АВ, лежащий на плоскости, виден под любым (переменным) острым углом, а данный отрезок CD виден под данным тупым углом.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
III. Упражнения и задачи для самостоятельной работы. 1.Отрезок постоянной длины 2а скользит своими концами по осям прямоугольной декартовой системы координат ху
1.Отрезок постоянной длины 2а скользит своими концами по осям прямоугольной декартовой системы координат ху. Составить параметрические и неявное уравнения в декартовых координатах, а также полярное уравнение кривой, являющейся траекторией основания перпендикуляра, опущенного из начала координат на этот отрезок (четырехлепестковая роза (см. рис.7) ). Сделать эскиз кривой.
2. Вокруг точки окружности радиуса а вращается луч. На этом луче по обе стороны от точки его пересечения с окружностью откладываются отрезки длины 2b (а¹b). Составить уравнение кривой, описываемой концами этих отрезков (улитка Паскаля (см. рис.8 ). Сделать эскиз кривой.
3. Пусть луч OL вращается с постоянной угловой скоростью
вокруг точки О, а точка М движется вдоль луча OL, удаляясь от начала О со скоростью, пропорциональной (с коэффициентом k) расстоянию ОМ. Найти уравнение кривой, описываемой точкой М (логарифмическая спираль (см. рис.14)). Сделать эскиз кривой.
4. Найти уравнение плоской кривой, обладающей тем свойством, что отрезок любой ее касательной между точкой касания и фиксированной прямой l постоянен и равен а (трактриса(см. рис. 16)). Сделать эскиз кривой.
5. Прямая OL, не перпендикулярная оси z, равномерно вращается вокруг нее с постоянной угловой скоростью
. Точка М движется по прямой OL с постоянной скоростью
. Найти уравнение кривой, являющейся траекторией точки М (коническая винтовая линия (см. рис. 22)). Сделать эскиз кривой.
6. Дана окружность радиуса а и касательная к ней в точке А. Из диаметрально противоположной точки О проведен луч, пересекающий окружность в точке С, а заданную касательную в точке В. На нем отложен отрезок ОМ, равный отрезку ВС. Найти полярное, параметрические и неявное уравнения траектории точки М (циссоида Диоклесса (см. рис.2)). Сделать эскиз этой кривой.
7. Прямая х=а пересекает ось х в точке А, а произвольный луч ОВ — в точке В. На луче по обе стороны от точки В отложены отрезки
, равные отрезку АВ. Найти полярное, параметрические и неявное уравнения кривой, состоящей из всех точек
(строфоида(см. рис.3)). Сделать эскиз кривой.
8. Составить уравнение кривой, описываемой точкой М окружности радиуса r, которая катится без скольжения по окружности радиуса R, оставаясь вне ее (эпициклоида (см.рис.10)) . Какая получится кривая при r = R? Сделать эскизы кривых.
9. Составить уравнение кривой, описываемой точкой М окружности радиуса r, которая катится без скольжения по окружности радиуса R, оставаясь внутри ее (гипоциклоида (см. рис.11)). Какая получится кривая при R=4r? Сделать эскизы кривых.
10. Движение точечного электрического заряда в магнитном поле с напряженностью
определяется дифференциальным уравнением
— радиус-вектор точки, в которой находится заряд, t — время, c=const. Доказать, что если заряд движется под действием магнитного поля с постоянной напряженностью
, то его скорость постоянна по величине, а его траекторией может быть лишь какая-либо из следующих линий:
1) прямая, коллинеарная вектору
;
2) окружность в плоскости, ортогональной
;
3) винтовая линия с осью, коллинеарной
.
Видео:Отрезок, луч, прямаяСкачать
Циссоида Диоклеса
1. Особенности формы. Среди многих способов образования циссоиды—кривой, открытой древними в поисках решения знаменитой задачи об удвоении куба, мы остановимся сначала на простейшем. Возьмем окружность (называемую производящей) с диаметром ОА=2а и касательную АВ к ней. Через точку О проведем луч ОВ и на нем отложим отрезок ОМ=ВС. Построенная таким образом точка М принадлежит циссоиде. Повернув луч 0В на некоторый угол и проделав указанное построение, мы найдем вторую точку циссоиды, и т. д. (Рис. 3).
Если точку О принять за полюс, то
но
откуда получаем полярное уравнение циссоиды
(1)
Пользуясь формулами перехода от полярных координат к декартовым, найдем уравнение циссоиды в прямоугольной системе:
(2)
Параметрические уравнения циссоиды можно получить, полагая x=ty, тогда, на основании уравнения (2), придем к системе
Уравнение (2) показывает, что циссоида является алгебраической кривой 3-го порядка, а из уравнений (3) следует, что она является рациональной кривой.
Циссоида симметрична относительно оси абсцисс, имеет бесконечные ветви; касательная к производящей окружности, т. е. прямая х = 2а, служит для нее асимптотой; начало координат является точкой возврата 1-го рода.
2. Свойства. Кинематически циссоида может быть получена как траектория середины М катета ВС треугольника АВС, передвигающегося в плоскости чертежа так, что его вершина В скользит по оси ординат, а другой катет АС всегда проходит через неподвижную точку Е на оси абсцисс. (Рис. 4)
Действительно, обозначив середину отрезка ОЕ через D , замечаем, что поскольку ВС=ЕО, ê ВСЕ= ê ВЕО, откуда /_ ВЕО = /_ СВЕ, и, следовательно, ê NBE — равнобедренный, а так как Е D =ЕО/2=ВС/2=ВМ, то отрезок DM параллелен отрезку BE . Пусть, далее, точка К есть точка пересечения с продолжением отрезка DM прямой, проходящей через точку В параллельно оси абсцисс. Опишем окружность с центром в начале координат и радиусом, равным OD, и проведем к ней касательную во второй точке пересечения с прямой ЕО. Она пройдет, очевидно, через точку К. Обозначив точку пересечения прямой DMK с окружностью через F , заметим, что треугольники DOF и МВК равны между собой. Из равенства их следует, что DF = MK , а значит, и DM = FK . Последнее равенство и показывает, что геометрическое место точек М будет циссоидой.
Другие способы образования циссоиды основаны на ее соотношениях с параболой. Покажем в первую очередь, что циссоида является подэрой параболы относительно ее вершины.
– уравнение данной параболы. Уравнение касательной в произвольной точке М (x, h) этой параболы можно записать в виде
уравнение перпендикуляра, опущенного из
начала координат на эту касательную, будет
координаты точки N пересечения его с касательной определятся по формулам
(4)
Исключая из этих равенств параметр h, мы получим уравнение
выражающее циссоиду.
Заметим далее, что координаты точки, симметричной началу координат относительно касательной к параболе у 2 = 2рх, получатся, если правые части формул (4) удвоить, и, следовательно, определятся формулами
Исключая из этих равенств параметр h, мы снова получим циссоиду с уравнением
Отсюда следует, что циссоида является геометрическим местом точек, симметричных вершине параболы относительно ее касательных.
Следует заметить, что геометрическое место точек, симметричных началу координат относительно касательной к параболе, можно рассматривать как траекторию вершины другой параболы, одинаковой с данной, которая катится по данной параболе. Таким образом, возникает новый способ кинематического образования циссоиды как траектории вершины параболы, которая без скольжения катится по другой такой же параболе.
Остановимся на метрических свойствах циссоиды; при этом нам будет удобно пользоваться параметрическими уравнениями циссоиды в виде
Площадь, ограниченная циссоидой и ее асимптотой, равняется утроенной площади производящего круга; действительно,
Это соотношение получено было Гюйгенсом и независимо от него Ферма.
Определяя площадь криволинейного треугольника ОАМС (рис.5), найдем, интегрируя в границах
до
что она равна
Если теперь провести касательные в точках А и С к производящему кругу, то площадь криволинейного треугольника CMANC будет равна
Выражение, стоящее в правой части, определяет утроенную площадь криволинейного треугольника CLANC. Итак, пл. CMANC =3 пл. CLANC. Это соотношение было открыто также Гюйгенсом.
Объем тела, образованного вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат определится по формуле
Если учесть, что объем тора, получаемого от вращения производящего круга вокруг оси ординат, равняется
то из полученного результата следует, что объем тела, получаемого вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат, в пять раз больше объема тора, полученного от вращения производящего круга вокруг той же оси. Это соотношение было получено также Гюйгенсом.
Пусть теперь хс — абсцисса центра тяжести части плоскости, ограниченной циссоидой и ее асимптотой; тогда по теореме Гюльдена будем иметь V == U • 2pхс, где V и U—соответственно объем и площадь, которые были определены выше. Подставляя их значения
в соотношение Гюльдена, получим
Таким образом, центр тяжести части плоскости, ограничиваемой циссоидой и ее асимптотой, делит отрезок между вершиной и асимптотой на две части, отношение которых равно 5.
Это соотношение позволяет в свою очередь определить объем тела, полученного вращением циссоиды вокруг ее асимптоты. По теореме Гюльдена будем иметь
Этот результат можно истолковать также как объем тора, полученного от вращения производящего круга вокруг асимптоты. Таким образом, объем тела, полученного вращением циссоиды вокруг ее асимптоты, равен объему тора, полученного от вращения производящего круга. Это соотношение установлено впервые Слюзом.
Длина дуги циссоиды от ее вершины до точки с абсциссой х определится по формуле
3.Применение циссоиды к решению делосской задачи. Как уже говорилось, циссоида была открыта древними в поисках решения делосской задачи об удвоении куба. История возникновения этой задачи, согласно легенде, передаваемой Эратосфеном, такова: на острове Делосе жители страдали от мора, посланного им богами; по предсказанию оракула богов можно было умиротворить, удвоив объем жертвенника, имевшего форму куба. Суть задачи сводилась к определению ребра куба, объем которого был бы в два раза больше объема данного куба. Что касается самого повода постановки задачи, то справедливо полагать, что «пифия находилась скорее под внушением математиков, нежели вдохновлялась самим богом» (Цейтен), так как задача об удвоении куба являлась естественным перенесением в пространство планиметрической задачи о построении квадрата с площадью, в два раза большей площади данного квадрата, и, следовательно, могла скорее возникнуть в сознании математика, нежели в сознании оракула.
Открытие циссоиды для целей решения делосской задачи приписывается Диоклесу, жившему в 3 веке до нашей эры. Возможность найти графическим путем ребро куба с объемом, в два раза большим объема данного куба, усматривается из следующих соображений. Пусть b – ребро данного куба, а В – ребро искомого; тогда
и, следовательно,
Отсюда ясно, что графическое решение задачи должно свестись к построению
Перепишем для этой цели уравнение циссоиды в виде
Заметим далее, что прямая
отсекает от касательной отрезок (рис. 6)
(5)
и пересекает циссоиду в точке М, координаты которой удовлетворяют уравнению
Это уравнение можно рассматривать как уравнение прямой, проходящей через точку А (2а, 0) и отсекающей на оси ординат отрезок
(6)
Если теперь принять
и на оси ординат отложить отрезок ОС == 2, соединить затем точку С с точкой А(1, 0), а точку пересечения прямой СА с циссоидой соединить с точкой О и продолжить полученный отрезок до пересечения с касательной, то, как это следует из формул (5) и (6), отрезок AD и будет равен
Древние рассматривали только ту часть циссоиды, которая находится внутри производящего круга. Вместе с дугой окружности производящего круга эта часть образует фигуру, напоминающую лист плюща, откуда проистекает название кривой. Наличие бесконечных ветвей у циссоиды было установлено в 17 веке Робервалем и независимо от него Слюзом. Кинематический способ образования циссоиды с помощью треугольника приписывается Ньютону, который выполнил также спрямление циссоиды не только аналитическим путем, но и графическим.
Кардиоида
1.Уравнение. Кардиоиду можно определить как траекторию точки, лежащей на окружности круга радиуса r, который катится по окружности неподвижного круга с таким же радиусом. Она будет представлять собой, таким образом, эпициклоиду с модулем m, равным 1.
Это обстоятельство позволяет сразу же записать параметрические уравнения кардиоиды, заменяя в ранее приведенных параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:
(1)
Чтобы получить полярное уравнение кардиоиды, удобно принять за полюс точку А (рис.7), а полярную ось направить по оси абсцисс. Так как четырехугольник AOO1M будет равнобедренной трапецией, то полярный угол j точки М окажется равным углу поворота производящего круга, т. е. параметру t. Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через r sin t. Сокращая полученное таким образом равенство на sin t, получим полярное уравнение кардиоиды
По виду этого уравнения
можно заключить, что кардиоида является одной из улиток Паскаля. Она может быть определена, следовательно, как конхоида круга.
Переводя уравнение (2) в прямоугольную систему координат, получим:
(3)
Из этого уравнения следует, что кардиоида является алгебраической кривой 4-го порядка.
2. Свойства. Прежде всего, поскольку кардиоида является эпициклоидой с m=1, на нее можно перенести все свойства рассмотренных нами в предыдущем параграфе эпициклоид.
Вот эти свойства и характеристики.
1. Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположную точке касания кругов, а нормаль — через точку их касания.
2. Угол m, составляемый касательной к кардиоиде с радиусом-вектором точки касания, равен половине угла, образуемого этим радиусом-вектором с полярной осью. Действительно
Из этого соотношения непосредственно вытекает, что угол, составляемый касательной к кардиоиде с осью абсцисс, равняется
(как внешний угол треугольника AMN Рис.8). Располагая формулой
можно доказать, что касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс, взаимно перпендикулярны.
Действительно, так как
Заметим еще, что геометрическое место точек пересечения этих касательных есть окружность
Действительно, уравнение первой касательной на основании уравнений (1) кардиоиды, будет иметь вид
а второй касательной
Исключая из этих уравнений параметр, получим уравнение указанной окружности.
3. Радиус кривизны в произвольной точке кардиоиды определится по формуле
(4)
Можно показать также, что радиус кривизны равняется 2/3 полярной нормали N в заданной точке.
Действительно,
откуда на основании (4) получаем
Соотношение это может быть использовано для построения центра кривизны кардиоиды.
4. Эволюта кардиоиды, согласно общему свойству эволют эпициклоид, будет также кардиоидой, подобной данной, с коэффициентом подобия, равным 1/3, и повернутой относительно данной на угол 180°.
5. Длина дуги кардиоиды от точки А до произвольной точки М определится по формуле
(5)
Если длину дуги отсчитывать от точки А1, диаметрально противоположной точке А, то формула для определения длины дуги может быть записана в виде
(6)
6. Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид
(7)
7. Площадь, ограниченная кардиоидой, определится по формуле
и, как видно, равна ушестеренной площади производящего круга.
Длина всей кардиоиды определится по формуле
и, как видно, равна восьми диаметрам производящего круга. Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен
Поверхность тела, полученного от вращения кардиоиды вокруг ее оси, равняется
Мы видели, что кардиоида органически связана с окружностью. Она является конхоидой круга и эпициклоидой. Она имеет с окружностью и иной характер родства — кардиоида является подэрой окружности относительно точки, принадлежащей этой окружности.
Действительно, пусть ОМ есть перпендикуляр, опущенный на касательную к окружности с радиусом, равным 2r, проведенную в точке N.
Так как ОМ = OB + ВМ, или r == 2r cos j + 2r, то геометрическим местом точек М будет кардиоида с уравнением r = 2r (1 + cos j).
Заметим в заключение, что кардиоида относится также к семейству синусоидальных спиралей, и отдельные свойства ее повторяют общие свойства этих кривых. Из этих свойств следует, в частности, что инверсия кардиоиды, относительно точки возврата дает параболу.
Астроида
1. Свойства. Астроида, как и рассмотренная выше кривая Штейнера, является частным случаем гипоциклоид, а именно, гипоциклоидой с модулем m, равным 1/4. Она представляет собой, следовательно, траекторию точки, лежащей на окружности круга радиуса r, который катится по внутренней стороне другого, неподвижного круга, радиус R которого в четыре раза больше.
Параметрические уравнения астроиды можно получить, полагая в уравнениях гипоциклоиды, m=1/4. Вот эти уравнения:
где t, как и ранее, угол поворота производящего круга (рис. 10)
Исключая из уравнений (1) параметр t, получим:
(2)
Из уравнения (2) следует, что астроида является алгебраической кривой 6-го порядка.
Параметрические уравнения (1) астроиды можно привести к виду
(3)
Исключая из этих уравнений параметр t, получим часто употребляемый вид уравнения астроиды
(4)
Полагая в ранее выведенных общих соотношениях для циклоидальных кривых модуль
m = -1/4, получим соответствующие соотношения для астроиды:
1) радиус кривизны в произвольной точке астроиды определяется по формуле
(5)
2) длина дуги астроиды от точки А до произвольной точки M(t) определится по формуле
(6)
длина одной ветви равна
а длина всей кривой 6R;
3) для получения натурального уравнения астроиды заметим предварительно, что если началом отсчета длины дуги полагать не точку А, для которой t = 0, а точку, для которой t = p, то длина дуги определится формулой
(6)
исключая параметр t из уравнений (5) и (6), получим натуральное уравнение астроиды
4) эволюта астроиды есть также астроида, подобная данной, с коэффициентом подобия, равным 2, повернутая относительно данной на угол p/4 (рис.11)
5) площадь, ограниченная всей астроидой, равна
объем тела, полученного от вращения астроиды, равняется 32/105pR 3
поверхность тела, образованного вращением астроиды, равна
Обратимся теперь к рассмотрению некоторых частных свойств астроиды.
Астроида является огибающей отрезка постоянной длины, концы. которого скользят по двум взаимно перпендикулярным прямым.
Принимаем эти прямые за оси координат и, обозначая угол наклона скользящего отрезка ND=R через a (рис.12), будем иметь уравнение прямой ND в виде
(7)
Дифференцируя это уравнение по параметру a, получим:
Исключая из последнего уравнения и уравнения (7) параметр a, будем иметь уравнение огибающей в виде
т. е. астроиду.
Практически перемещение отрезка ND можно осуществить с помощью так называемых кардановых кругов. Один из этих кругов с радиусом R неподвижен, а другой, с радиусом r, в два раза меньшим, катится по внутренней стороне неподвижного круга. Любые две диаметрально противоположные точки N и D катящегося круга будут перемещаться по двум взаимно перпендикулярным диаметрам Ох и Оу неподвижного круга. Ясно, что огибающей диаметра катящегося круга и будет астроида.
Рис. 11
Рис. 12
Рассмотренный способ образования астроиды можно истолковать также следующим образом. Прямоугольник ODCN, две стороны которого лежат на двух взаимно перпендикулярных прямых, деформируется так, что диагональ его сохраняет длину, равную R, огибающая диагонали и будет астроидой. Так как при этом перпендикуляр, опущенный из вершины С на диагональ DN, служит нормалью к огибающей, то астроида представляет собой геометрическое место оснований перпендикуляров, опущенных из вершины С прямоугольника на его диагональ.
2. Свойства касательных к астроиде. Уравнение (7) выражает прямую ND, т. е. касательную к астроиде в некоторой точке М, причем параметр a представляет собой угол, составляемый этой касательной с осью абсцисс. Уравнение другой касательной, перпендикулярной к первой, будет иметь вид
(8)
Исключая из уравнений (7) и (8) параметр а, получим уравнение
или, в полярной системе,
которое выражает четырехлепестковую розу. Итак, геометрическое место вершин прямого угла, стороны которого касаются астроиды, есть четырех лепестковая роза.
Другое свойство касательных к астроиде таково: каждая касательная пересекает астроиду в двух точках, касательные в которых пересекаются в точке, лежащей на окружности описанного около астроиды круга.
Определим подэру астроиды относительно точки Р, лежащей на биссектрисе 1-го координатного угла на расстоянии ОР=с от начала координат. Выше было показано, что астроиду можно рассматривать как огибающую отрезка ND = R, скользящего своими концами по координатным осям. Отсюда
следует, что искомую подэру можно определить как геометрическое место оснований перпендикуляров, опущенных из точки Р на прямую ND (рис. 13). Проведем ОЕ _|_ ND, и OQ, где Q — середина отрезка ND. Точку Р посчитаем полюсом, а прямую РК полярной осью. Полярный угол КРМ точки М подэры обозначим через j, а радиус-вектор РМ — через r. Тогда, как легко видеть, угол
Так как
Но, с другой стороны,
На основании последних двух равенств, полярное уравнение подэры запишется в виде
а в прямоугольной системе с началом в точке Р в виде
Полученная таким образом кривая 6-го порядка имеет в начале координат четырехкратную точку и называется «жуком». В частном случае, пои с=0, жук становится розой,
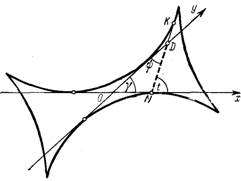
3. Косая астроида. Обобщением рассмотренной астроиды является так называемая косая астроида, которая представляет собой огибающую отрезка ND постоянной длины R, скользящего своими концами по двум прямым, пересекающимся под произвольным углом f.
Полагая эти пересекающиеся прямые координатными осями, обозначим угол, составляемый прямой ND с осью абсцисс, через t. Тогда из треугольника OND (рис. 14) будем иметь:
и следовательно, уравнение прямой ND в отрезках на осях запишется в виде
Дифференцируя это уравнение по t и исключая из полученного после дифференцирования равенства и уравнения прямой параметр t, получим параметрические уравнения косой астроиды в виде
при
эти уравнения выражают рассмотренную ранее прямую астроиду.
📸 Видео
Длина отрезкаСкачать
Уравнения прямой на плоскости | Векторная алгебраСкачать
Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
2. Уравнение плоскости примеры решения задач #1Скачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать
Геометрия 7 класс. УРОК 2. ОТРЕЗОК. Теория+задачиСкачать
11. Прямая в пространстве и ее уравненияСкачать
Измерение отрезковСкачать
Точки и прямые. Отрезок и его длина - геометрия 7 классСкачать
Аналитическая геометрия на плоскости. Решение задачСкачать
Задачи на отношение. Как решать и оформлять на примере свойства длины отрезка. Геометрия 7 класс.Скачать
Задача про соотношение сторон. Геометрия 7 класс.Скачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Видеоурок "Уравнение плоскости в отрезках"Скачать



 вокруг точки О, а точка М движется вдоль луча OL, удаляясь от начала О со скоростью, пропорциональной (с коэффициентом k) расстоянию ОМ. Найти уравнение кривой, описываемой точкой М (логарифмическая спираль (см. рис.14)). Сделать эскиз кривой.
вокруг точки О, а точка М движется вдоль луча OL, удаляясь от начала О со скоростью, пропорциональной (с коэффициентом k) расстоянию ОМ. Найти уравнение кривой, описываемой точкой М (логарифмическая спираль (см. рис.14)). Сделать эскиз кривой. . Точка М движется по прямой OL с постоянной скоростью
. Точка М движется по прямой OL с постоянной скоростью  . Найти уравнение кривой, являющейся траекторией точки М (коническая винтовая линия (см. рис. 22)). Сделать эскиз кривой.
. Найти уравнение кривой, являющейся траекторией точки М (коническая винтовая линия (см. рис. 22)). Сделать эскиз кривой. , равные отрезку АВ. Найти полярное, параметрические и неявное уравнения кривой, состоящей из всех точек
, равные отрезку АВ. Найти полярное, параметрические и неявное уравнения кривой, состоящей из всех точек  (строфоида(см. рис.3)). Сделать эскиз кривой.
(строфоида(см. рис.3)). Сделать эскиз кривой. определяется дифференциальным уравнением
определяется дифференциальным уравнением  — радиус-вектор точки, в которой находится заряд, t — время, c=const. Доказать, что если заряд движется под действием магнитного поля с постоянной напряженностью
— радиус-вектор точки, в которой находится заряд, t — время, c=const. Доказать, что если заряд движется под действием магнитного поля с постоянной напряженностью 
 но
но  откуда получаем полярное уравнение циссоиды
откуда получаем полярное уравнение циссоиды (1)
(1)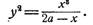 (2)
(2)

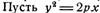 – уравнение данной параболы. Уравнение касательной в произвольной точке М (x, h) этой параболы можно записать в виде
– уравнение данной параболы. Уравнение касательной в произвольной точке М (x, h) этой параболы можно записать в виде  уравнение перпендикуляра, опущенного из
уравнение перпендикуляра, опущенного из
 координаты точки N пересечения его с касательной определятся по формулам
координаты точки N пересечения его с касательной определятся по формулам (4)
(4)
 выражающее циссоиду.
выражающее циссоиду.
 Отсюда следует, что циссоида является геометрическим местом точек, симметричных вершине параболы относительно ее касательных.
Отсюда следует, что циссоида является геометрическим местом точек, симметричных вершине параболы относительно ее касательных.


 до
до  что она равна
что она равна  Если теперь провести касательные в точках А и С к производящему кругу, то площадь криволинейного треугольника CMANC будет равна
Если теперь провести касательные в точках А и С к производящему кругу, то площадь криволинейного треугольника CMANC будет равна 
 Выражение, стоящее в правой части, определяет утроенную площадь криволинейного треугольника CLANC. Итак, пл. CMANC =3 пл. CLANC. Это соотношение было открыто также Гюйгенсом.
Выражение, стоящее в правой части, определяет утроенную площадь криволинейного треугольника CLANC. Итак, пл. CMANC =3 пл. CLANC. Это соотношение было открыто также Гюйгенсом.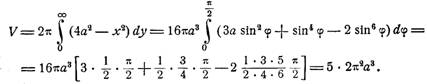
 то из полученного результата следует, что объем тела, получаемого вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат, в пять раз больше объема тора, полученного от вращения производящего круга вокруг той же оси. Это соотношение было получено также Гюйгенсом.
то из полученного результата следует, что объем тела, получаемого вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат, в пять раз больше объема тора, полученного от вращения производящего круга вокруг той же оси. Это соотношение было получено также Гюйгенсом.




 и, следовательно,
и, следовательно,  Отсюда ясно, что графическое решение задачи должно свестись к построению
Отсюда ясно, что графическое решение задачи должно свестись к построению 
 Заметим далее, что прямая
Заметим далее, что прямая  отсекает от касательной отрезок (рис. 6)
отсекает от касательной отрезок (рис. 6) (5)
(5)
 (6)
(6)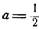 и на оси ординат отложить отрезок ОС == 2, соединить затем точку С с точкой А(1, 0), а точку пересечения прямой СА с циссоидой соединить с точкой О и продолжить полученный отрезок до пересечения с касательной, то, как это следует из формул (5) и (6), отрезок AD и будет равен
и на оси ординат отложить отрезок ОС == 2, соединить затем точку С с точкой А(1, 0), а точку пересечения прямой СА с циссоидой соединить с точкой О и продолжить полученный отрезок до пересечения с касательной, то, как это следует из формул (5) и (6), отрезок AD и будет равен 
 (1)
(1)

 (3)
(3)

 (как внешний угол треугольника AMN Рис.8). Располагая формулой
(как внешний угол треугольника AMN Рис.8). Располагая формулой 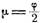 можно доказать, что касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс, взаимно перпендикулярны.
можно доказать, что касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс, взаимно перпендикулярны.

 Действительно, уравнение первой касательной на основании уравнений (1) кардиоиды, будет иметь вид
Действительно, уравнение первой касательной на основании уравнений (1) кардиоиды, будет иметь вид 
 а второй касательной
а второй касательной  Исключая из этих уравнений параметр, получим уравнение указанной окружности.
Исключая из этих уравнений параметр, получим уравнение указанной окружности. (4)
(4) откуда на основании (4) получаем
откуда на основании (4) получаем  Соотношение это может быть использовано для построения центра кривизны кардиоиды.
Соотношение это может быть использовано для построения центра кривизны кардиоиды. (5)
(5) (6)
(6) (7)
(7)






 (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) а длина всей кривой 6R;
а длина всей кривой 6R;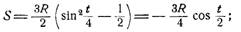 (6)
(6)
 объем тела, полученного от вращения астроиды, равняется 32/105pR 3
объем тела, полученного от вращения астроиды, равняется 32/105pR 3
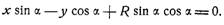 (7)
(7)
 т. е. астроиду.
т. е. астроиду. Рис. 11
Рис. 11 Рис. 12
Рис. 12 (8)
(8) или, в полярной системе,
или, в полярной системе,  которое выражает четырехлепестковую розу. Итак, геометрическое место вершин прямого угла, стороны которого касаются астроиды, есть четырех лепестковая роза.
которое выражает четырехлепестковую розу. Итак, геометрическое место вершин прямого угла, стороны которого касаются астроиды, есть четырех лепестковая роза.

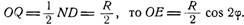
 На основании последних двух равенств, полярное уравнение подэры запишется в виде
На основании последних двух равенств, полярное уравнение подэры запишется в виде  а в прямоугольной системе с началом в точке Р в виде
а в прямоугольной системе с началом в точке Р в виде




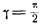 эти уравнения выражают рассмотренную ранее прямую астроиду.
эти уравнения выражают рассмотренную ранее прямую астроиду.















