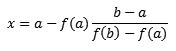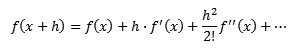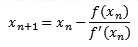Отделение и уточнение корней нелинейных уравнений паскаль (7 видео)

Решение нелинейных уравнений на языке программирования Pascal

Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.

Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.

Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.

Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.

Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:

После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.

Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.

В основе метода Ньютона лежит разложения функции в ряд Тейлора:

Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.

Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:

Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом

К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.

Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Отделение и уточнение корней нелинейных уравнений паскаль

Pers.narod.ru. Алгоритмы. Метод Ньютона решения нелинейного уравнения

В литературе называется также методом касательных.

Рассмотрим графическую иллюстрацию метода (рис. 1). Предположим, что графическим методом определено начальное приближение х₀ к корню. В точке х₀ вычислим левую часть решаемого уравнения f₀ = f(x₀), а также производную в этой точке f'(x₀) = tg α. Следующее приближение к корню найдем в точке х₁, где касательная к функции f(x), проведенная из точки (х₀, f₀), пересекает ось абсцисс. Затем считаем точку х₁ в качестве начальной и продолжаем итерационный процесс. Из рис. видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным х_k+1 и предыдущим х_k приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10 -5 — 10 -6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и её производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона (рис. 2).

Ниже приводится простая консольная программа на Паскале для решения алгебраического уравнения произвольной степени n>1 . Функция f(x) и первая производная f'(x) задаются подпрограммами-функциями f и f1 соответственно.

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Численные методы решение уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение задач на тему:

«Методы решения нелинейных уравнений».

1. отделить корни каждого из уравнений графически;

2. уточнить значение корней каждого их уравнений методом половинного деления отрезка с точностью до 0,001;

3.Уточнить какой-нибудь корень уравнения методом Ньютона с точностью до 0,001.

Уравнения должны быть рассмотрены на

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней ;

2. Уточнение корней до заданной точности.

Отделим корни графически, для этого запишем наше уравнение в сл. виде .

Построим графики этих функций. (т.е. и )

Из графика вы видим, что абсцисса точки пересечения этих графиков принадлежит отрезку .

Проверим, правильно ли мы нашли отрезок изоляции корня. Для этого подставим в уравнение (1.1) граничные значения отрезка. Тогда получим

Применим аналитическое отделение корней, основанное на следующей теореме:

Если непрерывная на отрезке [a, b] функция y = f(x) принимает на концах отрезка значения разных знаков, т.е. f(a)·f(b) , то внутри этого отрезка находится хотя бы один корень уравнения; если при этом производная сохраняет знак внутри отрезка [a, b], то корень является единственным.

В нашем случае Значит, по теореме представленной выше, мы получаем, что внутри отрезка находится хотя бы один корень уравнения.

Таким образом, корень отделен правильно.

2 0 .Воспользуемся методом половинного деления отрезка (дихотомии).

Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из методов решения нелинейных уравнений. Найдем корни уравнения (1.1) методом половинного деления.

1) Определим интервал на котором будем работать. В данном случае он задан: [-10;10]. (см.задание).

Найдем значения функции на концах этого интервала

2) Теперь мы будем искать середину нашего отрезка. Середина отрезка [ a ; b ] находится по сл.формуле

Если с=0, то нами найден корень уравнения. Если f(c) ≠ 0 , то в качестве нового отрезка изоляции корня [ a ₁ ; b ₁ ] выбираем ту половину [ a, c ] или [ c, b ], на концах которой f(x) принимает значения разных знаков. Другими словами, если

f(a) ∙ f(c) , то корень принадлежит отрезку [a, c],

f(a) ∙ f(c) > 0 — отрезку [ c, b ]

Полученный отрезок снова делим пополам, находим c ₁ ,вычисляем f(c ₁ ) , выбираем отрезок [ a ₂ , b ₂ ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие , то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять .

Начнем вычислять отрезки.

Замечание1: при вычислениях значений нам важен знак, а не само значение, поэтому при больших вычислениях можно исследовать функцию на знак, не вычисляя ее значения.

Для того, чтобы закрепить материал, составим алгоритм выполнения уточнения значения корней методом положительного деления отрезка.

Для проверки вычислений можно воспользоваться следующей программой (Pascal).

function f(x: real): real;

writeln (‘ Введите концы отрезка : ‘);

write (‘ a = ‘); readln ( a );

write (‘ b = ‘); readln ( b );

write (‘ Введите точность e = ‘); readln ( e );

while abs ( b — a ) > 2*e do

if f ( c ) = 0 then

writeln ( ‘ c = ‘ , c : 8 : 6 , ‘ f( c ) = ‘ , f( c ) : 8 : 6 );

writeln ( ‘ c = ‘ , c : 8 : 6, ‘f( c ) = ‘ , f( c ) : 8 : 6 );

3 0 . Метод Ньютона (метод касательных).

Этот метод применяется, если уравнение f ( x ) = 0 имеет корень x  [ a ; b ], и выполняются условия:

3)производные f ( x ) и f ( x ) сохраняют знак на отрезке [ a ; b ] (т.е. функция f ( x ) либо возрастает, либо убывает на отрезке [ a ; b ], сохраняя при этом направление выпуклости).

Основная идея метода заключается в следующем: на отрезке [ a ; b ] выбирается такое число x ₀, при котором f ( x ₀) имеет тот же знак, что и f ( x ₀), т. е. выполняется условие f ( x ₀)· f ( x )>0. Таким образом, выбирается точка с абсциссой x ₀, в которой касательная к кривой y = f ( x ) на отрезке [ a ; b ] пересекает ось O _x. За точку x ₀ сначала удобно выбирать один из концов отрезка.

Алгоритм решения задач с помощью метода Ньютона

— определяем интервал (если он не задан), которому будет принадлежать корень уравнения. Сужение интервала можно производить методом половинного деления.

— находим f ( x ) и f ( x ), причем f ( x )  0 при x [ a ; b ], f ( x ) и f ( x ) должны сохранять знак на отрезке [ a ; b ]

— выбираем один из концов отрезка [a,b] за x₀, исходя из того, что должно выполняться следующее условие

Решим уравнение данным методом.

Проверим, можем ли мы воспользоваться данным методом решения нелинейных уравнений.

1) функция (1.1) определена и непрерывна при x  (-  ; +  )

Начнем наши вычисления.

1) Определим интервал на котором мы будем работать. В данном случае, он нам задан: [-10,10]. (см. задание)

3) Выберем один из концов отрезка за х ₀ так, чтобы выполнялось условие (1.5)