Основные приемы решения квадратных уравнений и неравенств (3 видео)

Квадратные неравенства, примеры, решения

В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.

Содержание

Что представляет собой квадратное неравенство
Способы решения квадратных неравенств
Графический метод
Метод интервалов
Выделение квадрата двучлена
Неравенства, сводящиеся к квадратным
Алгебра и начала математического анализа. 10 класс
Квадратные уравнения и квадратичные неравенства с параметрами
💡 Видео

Видео:Решение квадратных неравенств | МатематикаСкачать

Что представляет собой квадратное неравенство

Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.

Квадратное неравенство – это такое неравенство, которое имеет вид a · x 2 + b · x + c 0 , где a , b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака может стоять любой другой знак неравенства.

Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y = a · x 2 + b · x + c .

Приведем пример квадратного неравенства:

Возьмем 5 · x 2 − 3 · x + 1 > 0 . В этом случае a = 5 , b = − 3 и c = 1 .

Или вот такое неравенство:

− 2 , 2 · z 2 − 0 , 5 · z − 11 ≤ 0 , где a = − 2 , 2 , b = − 0 , 5 и c = − 11 .

Покажем несколько примеров квадратных неравенств:

Здесь коэффициенты этого квадратного неравенства есть ; 1 2 3 · x 2 — x + 5 7 0 , в этом случае a = 1 2 3 , b = — 1 , c = 5 7 .

Особое внимание нужно обратить на тот факт, что коэффициент при x 2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b · x + c > 0 , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.

Пример такого неравенства x 2 − 5 ≥ 0 .

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Способы решения квадратных неравенств

Основным метода три:

графический;
метод интервалов;
через выделение квадрата двучлена в левой части.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Графический метод

Метод предполагает проведение построения и анализа графика квадратичной функции y = a · x 2 + b · x + c для квадратных неравенств a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Метод интервалов

Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.

Для неравенства a · x 2 + b · x + c 0 решениями являются промежутки со знаком минус, для неравенства a · x 2 + b · x + c > 0 , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.

Видео:Решение неравенства методом интерваловСкачать

Выделение квадрата двучлена

Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида ( x − p ) 2 q ( ≤ , > , ≥ ) , где p и q – некоторые числа.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Неравенства, сводящиеся к квадратным

К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.

Приведем пример. Рассмотрим равносильное преобразование неравенства 5 ≤ 2 · x − 3 · x 2 . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3 · x 2 − 2 · x + 5 ≤ 0 .

Необходимо найти множество решений неравенства 3 · ( x − 1 ) · ( x + 1 ) ( x − 2 ) 2 + x 2 + 5 .

Решение

Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:

3 · ( x − 1 ) · ( x + 1 ) − ( x − 2 ) 2 − x 2 − 5 0 , 3 · ( x 2 − 1 ) − ( x 2 − 4 · x + 4 ) − x 2 − 5 0 , 3 · x 2 − 3 − x 2 + 4 · x − 4 − x 2 − 5 0 , x 2 + 4 · x − 12 0 .

Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.

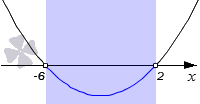
D ’ = 2 2 − 1 · ( − 12 ) = 16 , x 1 = − 6 , x 2 = 2

Построив график, мы можем увидеть, что множеством решений является интервал ( − 6 , 2 ) .

Ответ: ( − 6 , 2 ) .

Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14

равносильно квадратному неравенству x 2 − 6 · x − 9 0 , а логарифмическое неравенство log 3 ( x 2 + x + 7 ) ≥ 2 – неравенству x 2 + x − 2 ≥ 0 .

Видео:Решение квадратных неравенств графическим методом. 8 класс.Скачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №3. Квадратные уравнения, неравенства и их системы.

Перечень вопросов, рассматриваемых в теме:

систематизация знаний учащихся о решении квадратных уравнений и неравенств;
установление зависимости количества и расположения корней квадратного уравнения от его коэффициентов и значения дискриминанта;
способы решения квадратных уравнений и неравенств с параметрами.

Глоссарий по теме:

Параметр — (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода.

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М.: Просвещение, 2017.

Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.

Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.

Теоретический материал для самостоятельного изучения

В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.

На уроке будем рассматривать различные способы решения квадратных уравнений.

Как определить, сколько корней имеет уравнение, подскажет дискриминант.

Дискриминант – это число, которое находим по формуле

Если D 0 два корня.

Если дискриминант D> 0 , корни можно найти по формуле:

Если D = 0 , то

Рассмотрите пример. Решить уравнение

Шаг 1. Выпишем коэффициенты a, b, c.

Шаг 2. Найдем дискриминант. D=16.

Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:

1.Перед решением квадратного уравнения привести его к стандартному виду.

2. Избавьтесь от минуса перед . Для этого надо умножить всё уравнение на -1.

3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.

4. Проверяйте корни по теореме Виета. Это просто, когда a=1.

Рассмотрите другие формулы:

, где второй коэффициент b=2k – четное число.

Приведенное квадратное уравнение , старший коэффициент равен a= 1, проще решать по теореме Виета.

Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.

Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.

Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.

Рассмотрим несколько примеров:

Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.

Применяем метод сложения. Выполнив сложение, получаем уравнение , далее x= ±5. Находим у= ±2. Составляем возможные пары чисел.

Записываем ответ: (5; 2), (5; -2), (-5; 2), (- 5; -2).

Пример 3. Иногда проще ввести новые переменные.

Пусть xy=u, x+y=v. Тогда систему можно записать в более простом виде:

Решение смотри в примере 1.

Часть 2. Квадратные неравенства.

Теперь, когда мы разобрали решение квадратных уравнений, переходим к решению квадратных неравенств
ax^2+ bx + c больше или меньше нуля.

Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».

Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.

Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.

Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.

Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:

если а>0 + — +, если а 0 ветви вверх. Парабола выше оси, все значения положительны, значит х- любое число. Неравенство не имеет решений.

Далее рассмотрим схему решения системы неравенств.

Алгоритм решения системы неравенств.

1.Решить первое неравенство системы, изобразить его графически на оси x.

2.Решить второе неравенство системы, изобразить его графически на оси x.

3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Первый шаг в решении — найти особое значение параметра.

Второй шаг – определить допустимые значения.

Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.

Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.

Рассмотрите примеры решения неравенства с параметром.

Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.

Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.

Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.

Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.

Задания тренировочного модуля с разбором.

При каких значениях параметра, а квадратное уравнение

имеет только один корень?

Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.

Определите, на каком интервале значения квадратного трехчлена отрицательны?

Решаем неравенство: . Находим дискриминант квадратного трехчлена D= 1-4∙2∙ (-1) =1+8=9. Находим корни . Расставляем точки на числовой прямой.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого: