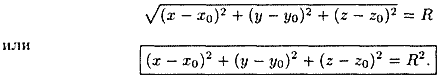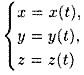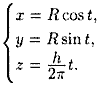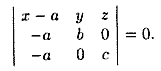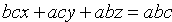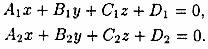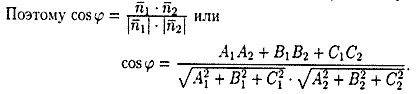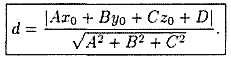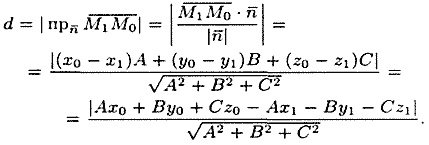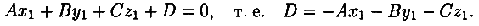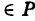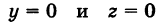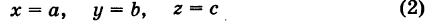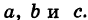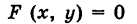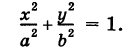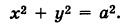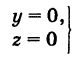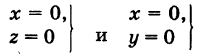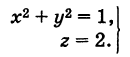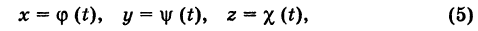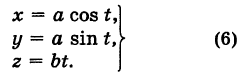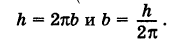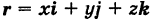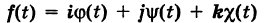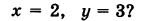Основные поверхности пространства и их уравнения (4 видео)

Лекция № 10

Содержание

Ссылки
Уравнения поверхности и линии в пространстве с примерами решения
Уравнения поверхности и линии в пространстве
Поверхности и линии в пространстве и их уравнения
Поверхности и линии в пространстве и их уравнения
Примеры решения и задачи с методическими указаниями
🔍 Видео

Ссылки

Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

12.1. Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О₁ есть геометрическое место всех точек пространства, находящихся от точки O₁ на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M₁(x₁;y₁;z₁) на данной поверхности, достаточно подстав и ть координаты точки M₁ в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.

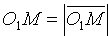
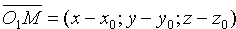
Найдем уравнение сферы радиуса R с центром в точке O₁(x₀;y₀;z₀). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O₁(x₀;y₀;z₀) равно радиусу R, т. е. O₁M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο₁ совпадает с началом координат, то уравнение сферы принимает вид .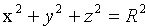

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

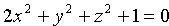
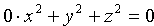
Так, уравнению не удовлетворяют никакие действительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).

Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве

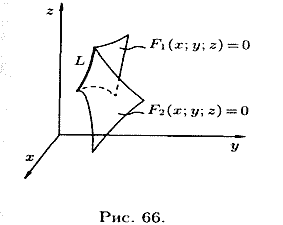
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.

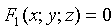
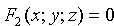
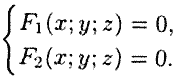
Если и — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

(12.1)

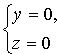
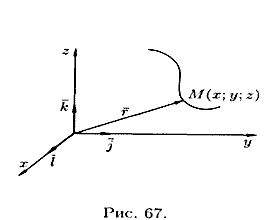
Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, есть уравнения оси Ох.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

(12.2)

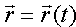
или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

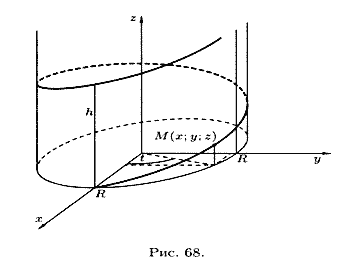
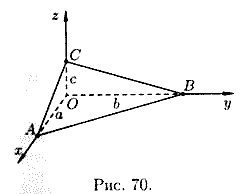
Например, параметрические уравнения винтовой линии имеют вид

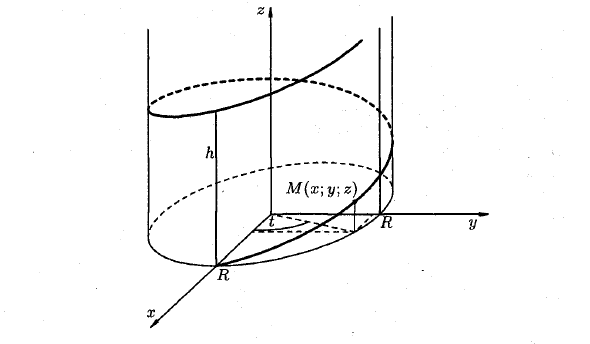
Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

12.2. Уравнения плоскости в пространстве

Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

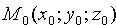
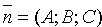
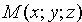
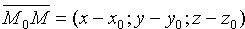
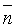
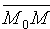
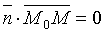
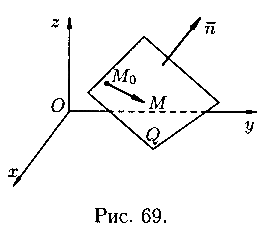
Пусть в пространстве Oxyz плоскость Q задана точкой и вектором , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку и составим вектор . При любом расположении точки Μ на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: , т. е.

(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).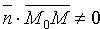

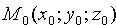
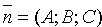
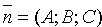
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку 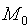. Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:

(12.4)

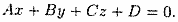
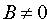
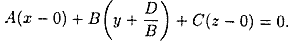
Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например , перепишем уравнение (12.4) в виде

(12.5)

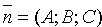
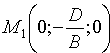
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором , проходящей через точку .

Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.

Частные случаи общего уравнения плоскости:

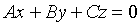
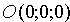
1. Если D = 0, то оно принимает вид . Этому уравнению удовлетворяет точка . Следовательно, в этом случае плоскость проходит через начало координат.

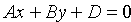
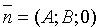
2. Если С = 0, то имеем уравнение . Нормальный вектор перпендикулярен оси Οz. Следовательно, плоскость параллельна оси Οz; если B = 0 — параллельна оси Оу, А = 0 — параллельна оси Ох.

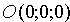
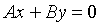
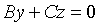
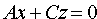
3. Если С = D = 0, то плоскость проходит через параллельно оси Οz, т. е. плоскость проходит через ось Οz. Аналогично, уравнениям и отвечают плоскости, проходящие соответственно через оси Ох и Оу.

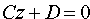
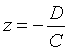
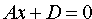
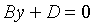
4. Если А = В = 0, то уравнение (12.4) принимает вид , т. е. Плоскость параллельна плоскости Оху. Аналогично, уравнениям и отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.

5. Если A = B = D = 0, то уравнение (12.4) примет вид 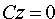, т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение плоскости Οxz; x = О — уравнение плоскости Oyz.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M₁(x₁;y₁;z₁), М₂(x₂;y₂;z₂) и М₃(х₃,y₃,z₃), не лежащие на одной прямой.

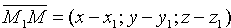
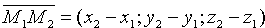
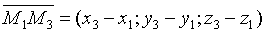
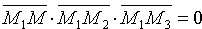
Возьмем на плоскости произвольную точку M(x;y;z) и составим векторы , , . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем , т. е.

(12.6)

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках

Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

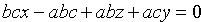
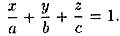
Раскрыв определитель, имеем , т. е. или

(12.7)

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора 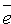, имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

Пусть ОК = p, а α, β, g — углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости Q проекция радиус-вектора на направление вектора всегда равно р: , т. е. или

(12.8)

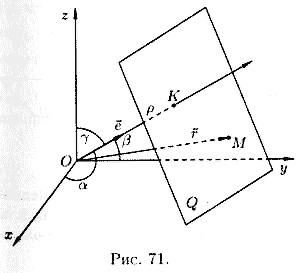
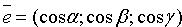
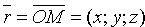
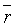
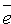
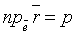
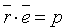
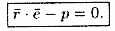
Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде

(12.9)

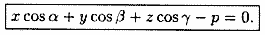
Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на нормирующий множитель 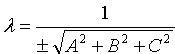, где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

12.3. Плоскость. Основные задачи

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть заданы две плоскости Q₁ и Q₂:

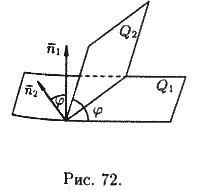
Под углом между плоскостями Q₁ и Q₂ понимается один из двугранных углов, образованных этими плоскостями.

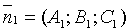
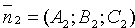
Угол j между нормальными векторами и плоскостей Q₁ и Q₂ равен одному из этих углов (см. рис. 72).

Для нахождения острого угла следует взять модуль правой части.

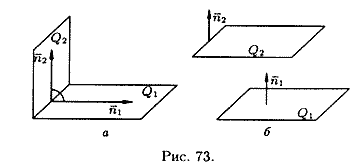
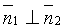
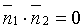
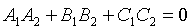
Если плоскости Q₁ и Q₂ перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. (и наоборот). Но тогда , т. е. . Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.

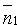
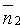
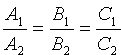
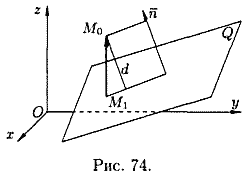
Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормали и (и наоборот). Но тогда, как известно координаты векторов пропорциональны: . Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂.

Расстояние от точки до плоскости

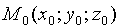
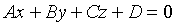
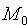
Пусть задана точка и плоскость Q своим уравнением . Расстояние d от точки до плоскости Q находится по формуле

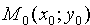
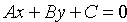
Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой .

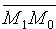
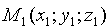
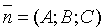
Расстояние d от точки M₀ до плоскости Q равно модулю проекции вектора , где — произвольная точка плоскости Q, на направление нормального вектора (см. рис. 74). Следовательно,

А так как точка 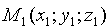принадлежит плоскости Q, то

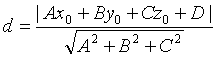
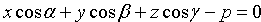
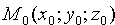
Поэтому . Отметим, что если плоскость Q задана уравнением , то расстояние от точки до плоскости Q может быть найдено по формуле

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

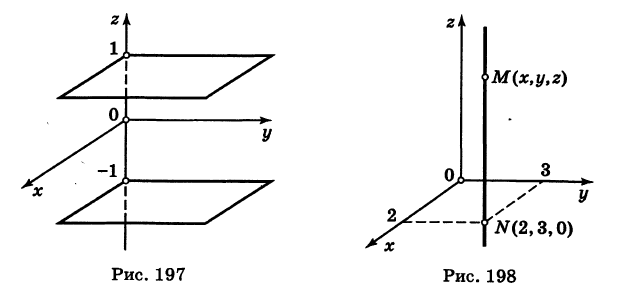
Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

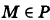
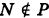
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

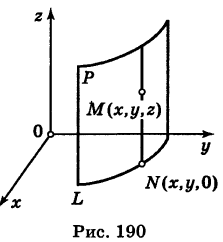
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 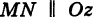(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

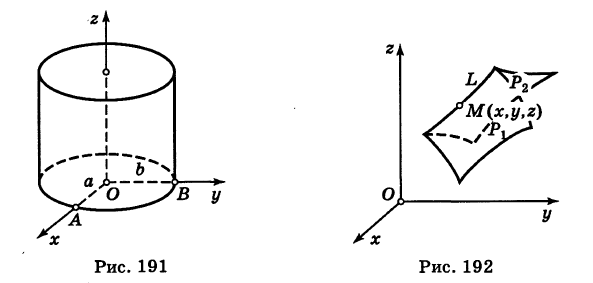
Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

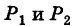
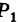
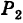
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

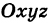
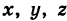
Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

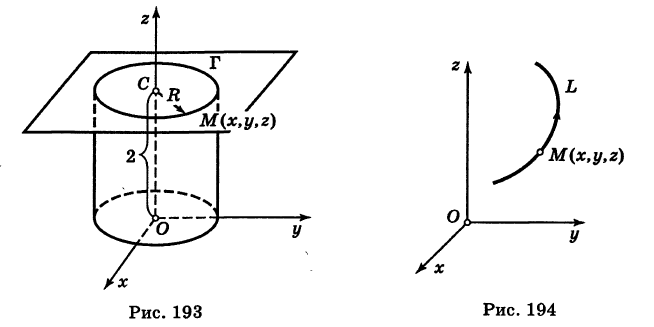
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

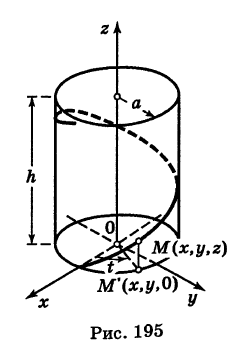
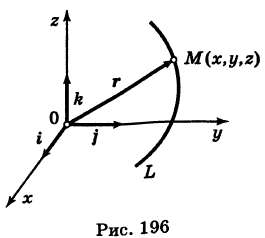
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 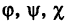— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

Написать уравнения винтовой линии радиуса а и шага 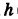(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 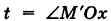и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

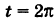
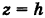
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

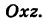
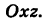
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

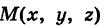
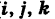
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

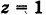
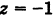
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Общее уравнение плоскости
Угол между плоскостями
Понятие о производной вектор-функции
Криволинейные интегралы
Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Поверхности и линии в пространстве и их уравнения

Видео:Поверхности второго порядкаСкачать

Поверхности и линии в пространстве и их уравнения

ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ И ИХ УРАВНЕНИЯ 1. Поверхность и ее уравнение. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке 0 есть геометрическое место всех точек пространства, находящихся от точки 0 на расстоянии R. Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и г -. Их координаты Свойства, общая все точки поверхности, можно записать в виде уравнения, связывающая координата всех точек поверхности.

которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой Поверхностные координаты, точки и z в уравнении Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение Р (х, у, г) = 0 с тремя переменными х, у и г, Людмила Фирмаль

И не удовлетворяю Если центр сферы 0 соответствует точке начала координат, то уравнение сферы принимает вид х2 -4у2 4-2 -4у Если такое же дано уравнение вида F (x; у; z) = 0, то оно, вообще говоря, определяется в пространскопне Выражение «вообще говоря» означает, что в отдельных случаях уравнение F (х у г) = 0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Говорят, «поверхность вырождается». . Так, уравнению 2х2 + у1 4- z2 4-1 = 0 не удовлетворяют никакие действительные значения гг, у, г Уравнению 0 • х2 4- у2 + z2 = 0 удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: 2 / = 0, z = 0, а ж-любое число). Итак, поверхность в пространстве может быть геометрической и аналитической. 1. Уравнение этой поверхности. 2. Дано уравнение F (x y z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве Fx (x-y z) = b F2 (x; y> z) = 0 Геометрия и геометрия Fx (x y z) = 0, F3 (®; y; *) = 0.Уравнение системы (1) 1-2 = 0

= О — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными Людмила Фирмаль

Траектории движения точки. (2) M (x y z) f = r (t) или параметрическими уравнениями х = х (т), У = 2 / (*), г = z (т) проекциями (2) на оси координат. Например, параметрические уравнения х = Я стоимость, у-R sin t, * = Если точка М равномерно двигается по образующей круговой цилиндру, а сам цилиндр равномерно вращается вокруг оси, то точка М описывает винтовая линия.