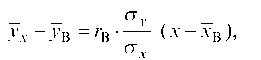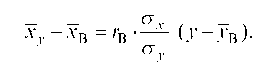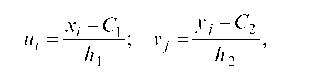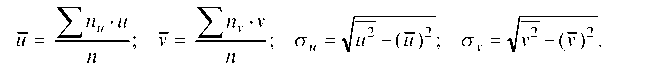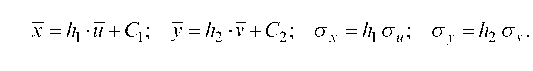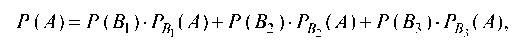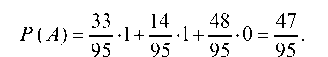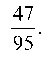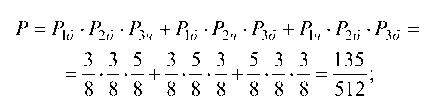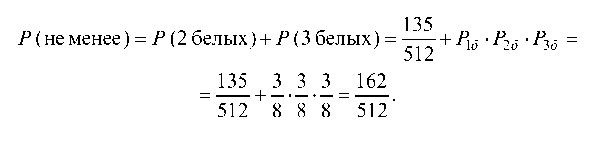Выборочные уравнения прямых линий регрессии y на x и x на y (4 видео)

Содержание

Корреляционная таблица
Выборочные уравнения прямых линий регрессии y на x и x на y
Контакты
6.7.2. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
📺 Видео

Видео:Математика #1 | Корреляция и регрессияСкачать

Корреляционная таблица

Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .

y/x	15	20	25	30	35	40
100	2	2
120	4	3	10	3
140	2	50	7	10
160	1	4	3
180	1	1

Решение:
Уравнение линейной регрессии с y на x будем искать по формуле

а уравнение регрессии с x на y, использовав формулу:

где x x , y — выборочные средние величин x и y, σ_x, σ_y — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 _x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 _y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и
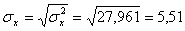
Определим коэффициент корреляции:

где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):

и уравнение x(y):

Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.

Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:

X / Y	2	4	6	8	10
1	5	4	2	0	0
2	0	6	3	3	0
3	0	0	1	2	3
5	0	0	0	0	1

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 _x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 _y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σ_x = 2.57 и σ_y = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:

Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
y_x = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
x_y = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим t_крит:
t_крит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.

Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение

Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.

Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4

Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7

Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение

Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.

X / Y	0	2	7	12	17	22	27	32	37	42
0	3	6	0	0	0	0	0	0	0	0
1	25	108	44	8	2	0	0	0	0	0
2	30	50	60	21	5	5	0	0	0	0
3	1	11	33	32	13	2	3	1	0	0
4	0	5	5	13	13	7	2	0	0	0
5	0	0	1	2	12	6	3	2	1	0
6	0	1	0	1	0	0	2	1	0	1
7	0	0	1	1	0	0	0	1	0	0

Решение.
Скачать решение

Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:

Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
Определить линии регрессии и построить их графики.

Скачать

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Выборочные уравнения прямых линий регрессии y на x и x на y

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

6.7.2. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным

При большом числе испытаний одно и то же значение X может встретиться nx раз, одно и то ж значение У может встретиться ny раз и одна и та же пара чисел (x; у) может встретиться nxy раз,

причем обычно— объем выборки.

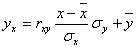
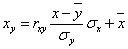
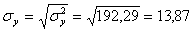
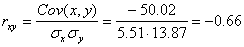
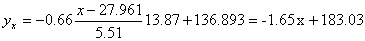
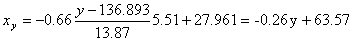
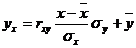
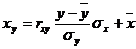
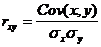
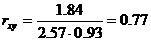
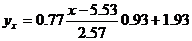
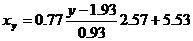
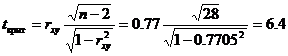
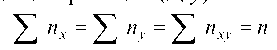Поэтому данные наблюденийГруппируют, т. е. подсчитывают nx, ny, nxy. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Если обе линии регрессии У на X и X на У — прямые, то корреляция является линейной.

Выборочное уравнение прямой линии регрессии У на X имеет вид:

Параметры pyx и В, которые определяются методом наименьших квадратов, имеют вид:

где yx — условная средняя; XВ и Ув — выборочные средние признаков X и У; —x и —у — выборочные средние квадратические отклонения; гВ — выборочный коэффициент корреляции.

Выборочное уравнение прямой линии регресии X на У имеет вид:

Считаем, что данные наблюдений над признаками X и У заданы в виде корреляционной таблицы с равноотстоящими вариантами.

Тогда переходим к условным вариантам:

где С1 — варианта признака X, имеющая наибольшую частоту; С 2 — варианта признака У, имеющая наибольшую частоту; h1 — шаг (разность между двумя соседними вариантами X); h2 — шаг (разность между двумя соседними вариантами У).

Тогда выборочный коэффициент корреляции

Величины u, v, su, sv могут быть найдены методом произведений, либо непосредственно по формулам

Зная эти величины, найдем параметры, входящие в уравнения регрессии, по формулам

12.1. Случайные события

12.1.1. В ящике находятся 6 одинаковых пар перчаток черного цвета и 4 одинаковых пары перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

Решение. Рассмотрим событие А — две извлеченные наудачу перчатки образуют пару; и гипотезы: B1 — извлечена пара перчаток черного цвета, B2 — извлечена пара перчаток бежевого цвета, B3 — извлеченные перчатки пару не образуют.

Вероятность гипотезы B1 по теореме умножения равна произведению вероятностей того, что первая перчатка черного цвета и вторая перчатка черного цвета, т. е.

Аналогично, вероятность гипотезы Bi равна:

Так как гипотезы B1, B2 и B3 составляют полную группу событий, то вероятность гипотезы B3 равна:

По формуле полной вероятности имеем:

где Pb (A) есть вероятность того, что пару образуют две черные перчатки и Pb1 (A) = 1; pB1 (A) — вероятность того, что пару образуют две бежевые перчатки и Pb2 (A) = 1; и, наконец, РВз( A) — вероятность того, что пару образуют перчатки разного цвета и

Таким образом, вероятность того, что две наудачу извлеченные перчатки образуют пару равна

12.1.2. В урне находятся 3 шара белого цвета и 5 шаров черного цвета. Наудачу по одному извлекают 3 шара и после каждого извлечения возвращают обратно в урну. Найти вероятность того, что среди извлеченных шаров окажется:

а) ровно два белых шара, б) не мене двух белых шаров.

Решение. Имеем схему с возвращением, т. е. каждый раз состав шаров не изменяется:

а) при извлечении трех шаров два из них должны быть белыми, а один черный. При этом черный может оказаться или первым, или вторым, или третьим. Применяя совместно теоремы сложения и умножения вероятностей, имеем:

б) вынуть не менее двух белых шаров означает, что белых шаров должно быть или два, или три:

12.1.3. В урне находятся 6 белых и 5 черных шаров. Три шара наудачу последовательно извлекаются без возвращения их в урну. Найти вероятность, что третий по счету шар окажется белым.

Решение. Если третий по счету шар должен быть белым, то первые два шара могут быть белыми, или белым и черным, или черным и белым, или черными, т. е. имеются четыре группы не-

совместных событий. Применяя к ним теорему умножения вероятностей, получим:

P = P1(5 • P2(5 • P3(5 + (P1(5 • Р2ч • P3(5 + P14 • P2(5 • P3(5 ) + Р1ч • Р2ч • P3(5 =

= A A 4 A A 5 A A 5 A A 6=540 = A

= П • 10 • 9 + И • 10 • 9 + И • 10 • 9 + И • 10 • 9 = 990 = IT