Основное уравнение радиолокации с пассивным ответом (6 видео)

Теоретические основи радиолокации

Содержание

Уравнение дальности радиолокации
Вывод уравнения радиолокации
Учет потерь
Влияние Земной поверхности
Отражение от плоской земной поверхности
Основное уравнение радиолокации. Дальность действия в свободном пространстве Выполнила: Темербекова А.Т. КТиТ-43 Проверила: Жумабаева А.С. — презентация
Похожие презентации
Презентация на тему: » Основное уравнение радиолокации. Дальность действия в свободном пространстве Выполнила: Темербекова А.Т. КТиТ-43 Проверила: Жумабаева А.С.» — Транскрипт:
Теория и техника радиолокации и радионавигации (стр. 24 )
ГЛАВА 8. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОСИСТЕМ
8.1. Дальность действия радиолиний
8.2. Обобщенное уравнение дальности радиолокационного
наблюдения в свободном пространстве
8.3. Погрешности измерения радионавигационного параметра
📽️ Видео

Уравнение дальности радиолокации

Уравнение дальности радиолокации (часто для краткости – уравнение радиолокации ) в простой и наглядной форме связывает между собой максимальную дальность действия радиолокатора, его параметры, а также параметры цели. В зависимости от требуемого результата уравнение радиолокации может быть записано относительно максимальной дальности действия радиолокатора или относительно мощности электромагнитной волны на входе приемной антенны. Во втором случае мощность P_e у приемной антенны радиолокатора выражается зависимостью от излучаемой мощности P_S , дальности цели R и отражающих характеристик цели, описываемых ее эффективной поверхностью рассеяния σ . Если известна чувствительность радиолокационного приемника, то с помощью уравнения радиолокации можно определить максимальную теоретически достижимую дальность действия радиолокатора. Таким образом, уравнение радиолокации может использоваться для оценки тактико-технических характеристик радиолокатора.

Вывод уравнения радиолокации

Прежде всего предположим, что распространение радиоволн происходит в идеальных условиях, то есть без потерь.

Рисунок 1. Плотность мощности, излучаемая ненаправленным излучателем, уменьшается при геометрическом расширении луча (при удалении от излучателя)

Если высокочастотная энергия излучается изотропным излучателем, то она распространяется равномерно во всех направлениях. Следовательно, поверхности с одинаковой плотностью мощности представляют собой сферы, площадь которых в зависимости от расстояния от излучателя определяется как ( A= 4 π R² ) . Одно и то же количество энергии с увеличением радиуса сферы распределяется на все большую площадь ее поверхности. Это означает, что плотность мощности электромагнитной волны на поверхности сферы обратно пропорциональна квадрату радиуса сферы. Таким образом, можно записать уравнение для вычисления плотности мощности S_u , излучаемой ненаправленным излучателем

P_S = излучаемая мощность [Вт]
R₁ = расстояние от передающей антенны до цели [м]

Рисунок 2: Усиление антенны, умноженное на плотность мощности, дает направленную плотность мощности.

Если же передающая антенна является направленной, то это приводит к увеличению плотности мощности, излучаемой в определенном направлении. Этот эффект называют усилением антенны. Таким образом, выражение для плотности мощности направленного излучателя S_g можно записать в виде

G = коэффициент усиления антенны.

Конечно, в действительности антенны радиолокаторов не являются «частично излучающими» изотропными излучателями. К антеннам радиолокаторов предъявляют требования малой ширины луча и коэффициента усиления на уровне 30 или 40 дБ (например, зеркальная параболическая антенна или фазированная антенная решетка).

Обнаружение цели зависит не только от плотности мощности в районе цели, а также от того, какая часть этой мощности отражается в направлении на радиолокатор. Для того, чтобы определить полезную отраженную мощность, необходимо знать эффективную поверхность рассеяния σ цели. Ее значение зависит от многих факторов, однако можно утверждать, что цель с большей площадью отражает больше мощности, чем цель с меньшей площадью. Это означает, что, при одинаковых условиях наблюдения пассажирский авиалайнер обладает большей площадью рассеяния, чем спортивный самолет.

Из приведенного выше следует, что отраженная от цели мощность P_r зависит от плотности мощности S_u , коэффициента усиления антенны G и изменяющейся эффективной поверхности рассеяния σ :

У упрощенном виде цель может рассматриваться как излучатель. При таком подходе отраженная мощность P_r рассматривается как излученная мощность.

Применив к отраженной мощности те же рассуждения, что и к излученной, по аналогии с формулой (1), можем записать выражение для плотности мощности S_e у приемной антенны:

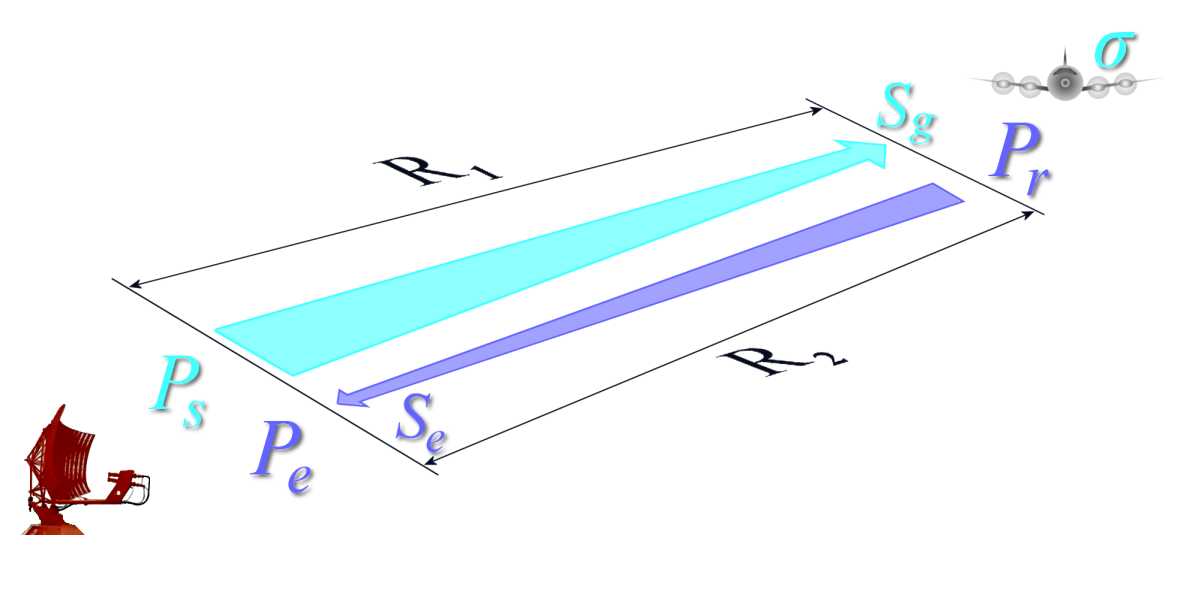
Рисунок 3. Связь между выражениями (3) и (4)

R₂ = расстояние между целью и приемной антенной.

Рисунок 3. Связь между выражениями (3) и (4)

Принятая в приемной антенне мощность P_e зависит от плотности мощности в точке приема S_e и эффективной площади антенны A_W .

Очевидно, что значение эффективной площади антенны характеризует ту часть мощности, которую антенна может «собрать» из всего потока мощности, отраженной от цели. Чем больше площадь антенны, тем больше мощности она может на себя «собрать». Кроме того, этот параметр обусловлен наличием потерь в антенне. По этой причине принятая антенной мощность не равна падающей на нее мощности. Эффективность антенны количественно описывают при помощи коэффициента эффективности K_a , значение которого для реальных антенн, как правило, составляет около 0,6 … 0,7.

Коэффициент эффективности антенны связывает между собой ее геометрическую и эффективную площадь, то есть

A = геометрическая площадь антенны [м²]

С учетом введенных величин выражение для принятой мощности P_e может быть записано в виде:

В приведенных выше выражениях излученная и отраженная волны рассматривались по отдельности. Следующим шагом является получение выражения, связывающего их параметры вместе. Для этого подставим выражение для отраженной мощности (3) в формулу для принятой мощности (8). В дальнейшем учтем, что для случая совмещенного радиолокатора R₁ = R₂ .

Коэффициент усиления антенны G может быть выражен через длину волны λ . Не приводя здесь вывода этого выражения, запишем окончательную формулу:

Выразив из (10) геометрическую площадь антенны А и подставив полученное выражение в (9), после упрощения получим:

Решая полученное уравнение относительно дальности цели R , мы получим классическое уравнение дальности радиолокации:

В полученном уравнении учитываются все величины, оказывающие влияние на распространение радиолокационных сигналов. Перед тем, как попробовать применить уравнение радиолокации на практике, например, для оценки эффективности радиолокатора, необходимо привести некоторые дополнительные соображения.

Для конкретного радиолокатора большинство параметров (в частности, P_s, G, λ ) можно считать постоянными, поскольку их значения изменяются в небольших пределах. С другой стороны, эффективная поверхность рассеяния изменяется достаточно сильно. Однако, для практических задач ее часто полагают равной 1 м².

Наименьшую принимаемую мощность, при которой отраженный сигнал может быть обнаружен, обозначают P_{E_min} . Сигналы меньшей, чем P_{E_min} мощности, не могут использоваться, поскольку они будут потеряны в шумах приемника. Поэтому P_{E_min} еще называют чувствительностью приемника. Значение P_{E_min} определяет максимальную дальность действия R_max радиолокатора:

Использование этого уравнения радиолокации позволяет легко объяснить влияние той или иной характеристики радиолокатора на дальность его действия.

Учет потерь

Приведенный выше вывод уравнения радиолокации выполнен в предположении идеальных условий распространения электромагнитных волн, то есть распространения без потерь. В реальности необходимо учитывать разнообразные потери, поскольку они могут существенно влиять на эффективность радиолокатора. С этой целью уравнение радиолокации дополняется коэффициентом потерь L_ges .

Этот коэффициент учитывает следующие потери:

L _D = внутренние потери в передающем и приемном трактах радиолокатора;
L _f = флуктуационные потери во время отражения от цели;
L _Atm = атмосферные потери – потери на поглощение электромагнитных волн при распространении их в атмосфере от радиолокатора до цели и обратно.

В высокочастотных компонентах радиолокатора, таких как волноводы, фильтры, а также в антенных обтекателях также возникают внутренние потери. Для конкретного радиолокатора эти потери относительно постоянны и могут быть легко измерены.

Атмосферное ослабление и отражение от поверхности Земли являются постоянными факторами.

Влияние Земной поверхности

Расширенная, однако реже используемая, форма записи уравнения радиолокации учитывает дополнительные факторы, такие как поверхность Земли, однако не учитывает чувствительность приемника и атмосферное ослабление.

В этом выражении, помимо уже известных величин, появляются следующие:

K_α – коэффициент потерь вместо L_ges.;
A_z – эффективная поверхность отражения вместо σ;
t_i – длительность импульса;
n_R – коэффициент шума приемника;
d – коэффициент четкости экрана индикаторного устройства;

R_e – толщина слоя поглощающей среды;
γ – угол отражения луча;
K – постоянная Больцмана;
T₀ – абсолютная температура в К;
δ_R – коэффициент ослабления в поглощающей среде.

Отражение от плоской земной поверхности

Геометрическое представление (Рисунок 3) поясняет влияние поверхности Земли. Плоскость Земли вблизи антенны радиолокатора оказывает существенное влияние на диаграмму направленности антенны в вертикальной плоскости. Взаимодействие прямой и переотраженной от поверхности грунта волн изменяет диаграмму направленности антенны на передачу и на прием. Это влияние значительно в диапазоне очень высоких частот (ОВЧ, VHF), к которому относятся частоты 30 … 300 МГц. С увеличением частоты такое влияние уменьшается. Для обнаружения маловысотных целей использование отражения от земной поверхности является необходимым. Однако это возможно, только если размеры неровностей поверхности в первой зоне Френеля (радиуса R_F ) относительно антенны не превышают значения 0,001· R_F (то есть, если радиус первой зоны Френеля R_F = 1000 м, то на этом расстоянии от антенны радиолокатора не должно быть неровностей больше 1 м!).

Рисунок 4. Геометрия отражений от земной поверхности

Специализированные радиолокаторы, работающие в диапазоне ОВЧ (VHF), используют отражение от земной поверхности для увеличения дальности действия на малых высотах. На больших высотах влияние этого отражения приводит к нежелательным эффектам, а именно, к изрезанности зоны обзора в вертикальной плоскости. На Рисунке 4 показано изменение формы диаграммы направленности антенны под влиянием отражения от земной поверхности. Изрезанность зоны обзора приводит к пропаданию сигнала от цели во время ее нахождения между лепестками. Указанный эффект использовался в наземных радиолокаторах управления воздушным движением, при этом лучшие результаты наблюдались на более низких частотах, где лепестки получались довольно широкими и обеспечивали достаточное покрытие на больших высотах. С увеличением рабочей частоты радиолокатора влияние отражения от земной поверхности на форму диаграммы направленности антенны в вертикальной плоскости ослабевает.

Рисунок 5. Диаграмма направленности антенны в вертикальной плоскости с учетом влияния отражений от земной поверхности.

Увеличение высоты антенны приводит к тому, что количество лепестков увеличивается и они становятся более узкими, тем самым уменьшается количество пропаданий сигнала от цели, двигающейся на постоянной высоте. Однако вместе с этим, увеличение высоты антенны приводит к увеличению размеров первой зоны Френеля, то есть зоны, существенной для формирования диаграммы направленности антенны. А это, в свою очередь, ужесточает требования к позиции радиолокатора.

Таким образом, отражение от земной поверхности может оказывать как позитивное, так и негативное влияние на эффективность функционирования радиолокатора. Степень этого влияния зависит от многих факторов, таких как длина волны, высота подъема антенны, наличие и размер неровностей поверхности позиции на расстоянии, соответствующем первой зоне Френеля. Отсюда следует, что для конкретного радиолокатора, когда на первые два фактора влиять не представляется возможным, особое значение приобретает выбор и подготовка позиции.

Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)

Видео:Дальность системы с пассивным ответом.Скачать

Основное уравнение радиолокации. Дальность действия в свободном пространстве Выполнила: Темербекова А.Т. КТиТ-43 Проверила: Жумабаева А.С. — презентация

Презентация была опубликована 4 года назад пользователемарн тем

Презентация на тему: » Основное уравнение радиолокации. Дальность действия в свободном пространстве Выполнила: Темербекова А.Т. КТиТ-43 Проверила: Жумабаева А.С.» — Транскрипт:

1 Основное уравнение радиолокации. Дальность дедедействия в свободном пространстве Выполнила: Темербекова А.Т. КТиТ-43 Проверила: Жумабаева А.С.

2 Что такое основное уравнение радиолокации?

3 Основным уравнением радиолокации называется уравнение, связывающее максимальную дальность дедедействия активной РЛС в свободном пространстве с ее основными техническими характеристиками и отражающей способностью объекта.

4 Допустим что.. В точке О расположен передатчик РЛС, излучающий импульсную мощность P I, а в точкеО 1, расположенной на расстоянии D от РЛС, находится отражающий объект(Рис.1). Рис.1. Определение максимальной дальности дедедействия РЛС.

5 Под дальностью дедедействия в свободном пространстве подразумевается дальность, зависящая от технических характеристик РЛС и от отражающих свойств объекта (цели). Влияние атмосферы, формы Земли и подстилающей поверхности в этом случае не учитывается.

6 Основное уравнение радиолокации

7 Мощность передатчика Мощность передатчика. Распространено заблуждение, что «мощность и дальность одно и то же». Две радиостанции с одинаковыми мощностями могут отличаться по дальности, например, в десять раз. Гораздо важнее мощности эффективность антенны, чувствительность приёмника и избирательность. Мощность же важна в присутствии электромагнитных помех, тогда увеличение мощности в 4 раза увеличит дальность связи примерно в 1,5 раза. В поле для увеличения дальности в 2 раза мощность надо увеличить в 24=16 раз.

8 Коэффициент напоравоенного де́дедействия антенны Коэффицие́нт напора́военного де́дедействия (КНД) антенны отношение квадрата напряженности поля, создаваемого антенной в данном напоравлении, к среднему значению квадрата напряженности поля по всем напоравлениям.

9 Эффективная площадь антенны Эффективная площадь антенны площадь эквивалентной плоской антенны с равномерным амплитудно- фазовым распределением, обладающей тем же максимальным значением коэффициента напоравоенного дедедействия, что и данная антенна.

10 Эффективная площадь рассеяния ЭПР является количественной мерой свойства объекта рассеивать электромагнитную волну

11 Чувствительность приемника Одним из важнейших показателей качества тракта приема является чувствительность приемника. Она характеризует способность приемника принимать слабые сигналы.

12 Основное уравнение показывает, что Максимальная дальность дедедействия РЛС в свободном пространстве зависит от параметров РЛС и отражающих свойств цели. Максимальная дальность дедедействия РЛС тем выше, чем больше излучаемая мощность передатчика, КНД антенны, ЭПР цели и чем меньше значение чувствительности приемника.

13 Выводы: 1. Увеличение максимальной дальности дедедействия РЛС возможно только за счет увеличения энергии зондирующих импульсов путем увеличения средней мощности передатчика (т.е. за счет увеличения мощности источника питания).

14 2. Увеличение дальности Дмакс в два раза достигается ценой увеличения мощности передатчика Рt или чувствительности приемника (уменьшения Рrмин) в 16 раз

15 3. Для увеличения дальности Дмакс в два раза достаточно увеличить площадь антенны в четыре раза 4. Дальность дедедействия не зависит от формы сигнала.

16 Влияния ВЛИЯНИЕ ВОДНОЙ (ЗЕМНОЙ) ПОВЕРХНОСТИ ВЛИЯНИЕ АТМОСФЕРЫСЖАТИЕ ИМПУЛЬСОВ

17 ВЛИЯНИЕ ВОДНОЙ (ЗЕМНОЙ) ПОВЕРХНОСТИ Водная или земная поверхность влияет на дальность дедедействия судовой навигационной РЛС из-за отражения электромагнитной энергии от подстилающей поверхности, а также вследствие сферичности Земли, ограничивающей дальность радиолокационного обнаружения.

18 ВЛИЯНИЕ АТМОСФЕРЫ Влияние атмосферы выражается в следующем: из-за атмосферной рефракции радиоволны отклоняются от прямолинейного распространения; поглощается и рассеивается энергия радиоволн в сантиметровом и миллиметровом диапазонах. Атмосферная рефракция, т.е. преломление радиоволн в нижних слоях атмосферы

19 СЖАТИЕ ИМПУЛЬСОВ Увеличение длительности зондирующих импульсов снижает разрешающую способность РЛС по дальности, уменьшает потенциальную точность измерения расстояний до объектов.

Видео:Распространение радиоволн. Радиолокация. 11 класс.Скачать

Теория и техника радиолокации и радионавигации (стр. 24 )

Основное уравнение радиолокации с пассивным ответом

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Вопросы для самоконтроля:

Вопрос 1. Каковы причины вторичного излучения различных радиолокационных целей?

Вопрос 2. Что характеризует поляризационная матрица рассеяния цели?

Вопрос 3. Дайте определение ЭПР цели и приведите общую формулу для ее расчета.

Вопрос 4. Почему диаграмма рассеяния уголкового отражателя значительно шире, чем плоского листа?

Вопрос 5. При каких условиях площадь поперечного сечения шара можно считать равной его ЭПР?

Вопрос 6. Что такое разрешаемый объем и разрешаемая площадь? В каких случаях их используют?

Изучив материал главы, ответьте на вопросы. При возникновении трудностей обратитесь к материалам для закрепления знаний в конце пособия. Для углубленного изучения воспользуйтесь литературой: основной: 1 – 3; дополнительной: 4 – 6 и повторите основные определения, приведенные в конце пособия.

Видео:Общие принципы работы радиолокатораСкачать

ГЛАВА 8. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОСИСТЕМ

Видео:Дальность действия радиосистем.Скачать

8.1. Дальность действия радиолиний

Дальность действия является одной из важнейших характеристик большинства радиосистем. Под дальностью действия понимают максимальное расстояние Dмакс, на котором принимаемый сигнал достигает минимально допустимого (порогового) уровня Рсмин, еще достаточного для выполнения системой основных функций с качественными показателями не хуже заданных.

Радиолиния с активным ответом. Радиолиния с активным ответом (рис. 4.3 а) состоит из двух радиолиний связи: линии запроса и линии ответа. Для каждой из них можно найти максимальную дальность действия по формуле

, (8.1)

, (8.2)

где G — коэффициент усиления антенн на излучение и прием, для запросчика и ответчика, соответственно;-

Pи – мощность излучения запросчиком и ответчиком соответственно;

Pс мин – чувствительность приемника запросчика и ответчика соответственно;

λi – длинна волы излучения соответственно запросчика и ответчика.

Результирующая дальность действия системы определяется радиолинией с меньшей дальностью действия. Стремятся сделать каналы запроса и ответа равнонадежными, а систему — сбалансированной, т. е. обеспечить Dз макс = Dо макс

Если в запросчике и ответчике для передачи и приема используют одну антенну, а частоты запросного и ответного сигналов близки, размеры антенн одинаковы, следовательно условие баланса системы:

Pиз / Pсз мин = Pио / Pсо мин (8.3)

Радиолиния с пассивным ответом. В этом случае ответный сигнал создается при рассеянии радиоволн облучаемым объектом с ЭПР σц, а запросчиком является передатчик РЛС или радиовысотомера. Предположим, что РЛС излучает зондирующий сигнал мощностью Ри, коэффициент усиления ее передающей антенны Gи, приемной Gп, эффективная площадь Ап = Gп λ 2и /(4π), чувствительность приемника Pс мин. При расстоянии от РЛС до цели D плотность потока мощности у цели

По определению ЭПР, вся эта мощность рассеивается целью изотропно; следовательно, плотность потока мощности у антенны РЛС на расстоянии D от цели П1 = Ри Gи / (4π D2), а мощность, перехватываемая целью P1 = П1 σц = Ри Gи σц / (4π D2) .По определению ЭПР, вся эта мощность рассеивается целью изотропно; следовательно, плотность потока мощности у антенны РЛС на расстоянии В от цели

П2 =P1 / (4π D2)= П1 σц / (4π D2)= Ри Gи σц / (4π )2 D4 ,

а мощность сигнала в антенне РЛС

Pc = П2 Ап= Ри Gи σц Ап / (4π )2 D4 = Ри Gи Gп σц λи 2 / (4π )3 D4

При увеличении дальности D мощность сигнала Рс падает, достигая порогового уровня Pс мин при

, (8.4)

Это выражение называют основным уравнением радиолокации или уравнением дальности РЛС в свободном пространстве. Оно отражает связь дальности действия РЛС с ее основными параметрами и ЭПР цели.

Параметры Pс мин и σц имеют статистический характер и зависят от многих факторов. В основном уравнении не учитываются потери при распространении сигнала, потери в антенно-фидерном и других устройствах РЛС при формировании, приеме и обработке сигнала.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

8.2. Обобщенное уравнение дальности радиолокационного

Видео:Урок 388. Радиолокация. Физические основы телевиденияСкачать

наблюдения в свободном пространстве

При расчете дальности радиолокационного наблюдения определенной цели используют среднее значение ее ЭПР (σц = ), а возможные флуктуации ЭПР учитывают при выборе модели принимаемого сигнала (видом флуктуации его амплитуды и фазы). Таким образом, для определения порогового сигнала Рсмин в уравнении (6.4) нужно знать характеристики сигнала и помех, заданные значения вероятности правильного обнаружения рпо и вероятности ложной тревоги pлт. При этом структура и характеристики приемника, устройств обработки и регистрации сигнала выбирают так, чтобы свести Рсмин к возможно низкому уровню, обеспечивающему максимальную дальность действия РЛС.

Рассчитаем Рсмин при воздействии помехи с равномерной спектральной плотностью N0.

Вероятность правильного обнаружения рпо и вероятность ложной тревоги рлт зависят от отношения сигнала к шуму на входе порогового устройства (параметра обнаружения q=Umc/σш) и выбранного порога, значение которого зависит от выбранного критерия обнаружения.

В радиолокации используют критерий Неймана-Пирсона, в соответствии с которым оптимальный приемник должен обеспечивать получение наибольшего значения рпо при заданном значении рлт. Нахождение минимального значения q = qмин при котором рпо еще не меньше заданного (рпо)зад, а вероятность ложной тревоги pлт не превышает допустимой, осуществляют с помощью характеристик обнаружения pno=f(q), представленных на рис. 3.6.

Для импульсной РЛС с зондирующим импульсом длительностью τи и точечной цели сигнал на входе приемника также имеет длительность τи, и при мощности сигнала Рс его энергия Eс = Рс τи.

Если амплитуда напряжения сигнала Umc, то при входном сопротивлении, равном 1 Ом, энергия сигнала Ec = Umc2 τи /2. Тогда параметр обнаружения

Представив мощность порогового сигнала Рсмин, входящую в основное уравнение радиолокации (6.4), через параметр обнаружения Рсмин =qмин2 N0 /(2 τи), можно при расчете максимальной дальности действия РЛС непосредственно использовать характеристики обнаружения. Отклонения характеристик приемника от оптимальных учитывают путем введения коэффициента потерь Lп > 1, который показывает, во сколько раз (на сколько децибел) следует увеличить мощность сигнала в реальной системе, чтобы обеспечить заданные параметры обнаружения. Таким образом, с учетом потерь выражение (6.4) принимает вид

, (8.5)

Уравнение дальности в этой форме называют обобщенным уравнением дальности или обобщенным уравнением радиолокации.

В том случае, когда источником помех являются шумы антенны мощностью РшА и собственные шумы приемника с приведенной к входу мощностью Ршп, полная мощность шумов на входе приемника

Рш = РшА + Ршп. . Если ширина полосы пропускания приемного тракта ∆f, а температура антенны ТА, то

РшА = k TА ∆f, где k= 1,38 10-23 Дж/К — постоянная Больцмана.

Обычно спектральную плотность шума N0 представляют через шумовую температуру Tш=TA + T0(kш — l), где kш = l + Pшn/PшА, — коэффициент шума приемника; Т0 = = 290 К. Таким образом,

Рш = k TА ∆f + k T0 ∆f (kш – l) = k ∆f[TA + T0(kш — l)] = k ∆fTш.

Считая спектр шума равномерным в полосе ∆f, N0 = РШ/∆f = = k Tш, найдем

. (8.6)

Коэффициент потерь Lп может быть представлен произведением элементарных коэффициентов потерь, учитывающих потери, вызванные затуханием сигнала в антенно-фидерном устройстве, несогласованностью АЧХ приемника со спектром сигнала, детектированием, нестабильностью частоты гетеродина приемника, сканированием ДНА и другими причинами.

Часто уравнение (8.6) представляют в логарифмической форме и все величины, в том числе и коэффициенты потерь, подставляют в децибелах, заменяя умножение параметров их суммированием, а деление — вычитанием. Анализируя уравнение (8.6), видим, что для увеличения Dмакс, например, в два раза, нужно увеличить энергию импульса в 16 раз, что соответствует 12 дБ. То же относится и к другим параметрам, входящим в формулы для первой степени.

В импульсных РЛС при передаче и приеме используют одну и ту же антенну, поэтому Gи = Gп = G. В результате формула принимает вид

. (8.7)

Следовательно, увеличения Dмакс в два раза можно достигнуть путем четырехкратного увеличения коэффициента усиления антенны. Следует подчеркнуть, что расчет Dмакс для реальных условий работы РЛС представляет собой сложную задачу. Кроме рассмотренных источников потерь должны быть учтены потери при распространении сигнала, а также влияние отражений от земной поверхности.

Видео:РЛССкачать

8.3. Погрешности измерения радионавигационного параметра

Точность измерения координат и параметров движения объекта является важнейшей характеристикой радиолокационных и радионавигационных систем. Она определяется погрешностями измерений радионавигационного параметра (РНП) — параметра радиосигнала, несущего информацию о координате или скорости объекта.

В дальномерных и разностно-далъномерных системах измеряемым параметром может быть временной, частотный или фазовый сдвиг колебаний принимаемого сигнала относительно опорного, формируемого в системе. Соответственно измеряемому параметру различают импульсные, частотные и фазовые системы. В угломерных системах РНП является угол между направлением на объект и опорным направлением, а в системах измерения скорости — доплеровское смещение частоты принимаемых колебаний относительно частоты опорных.