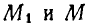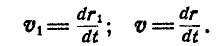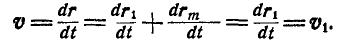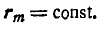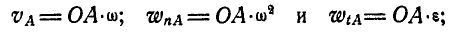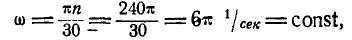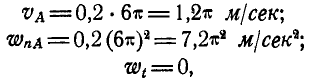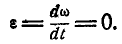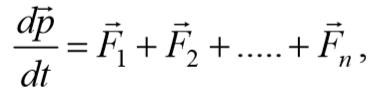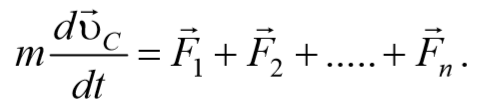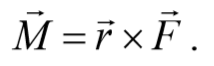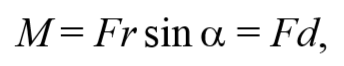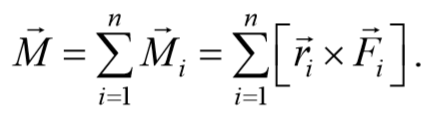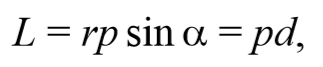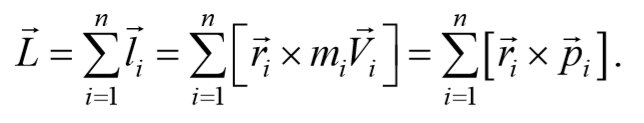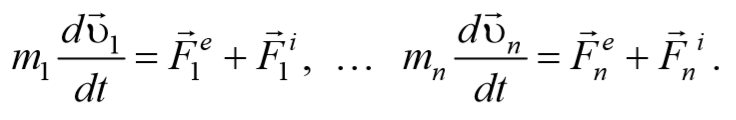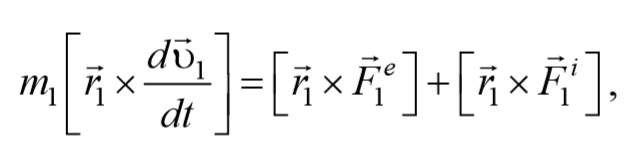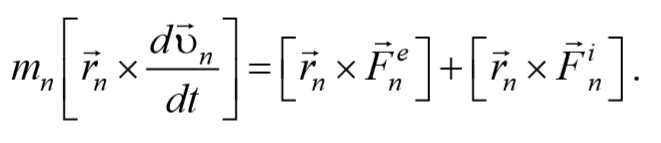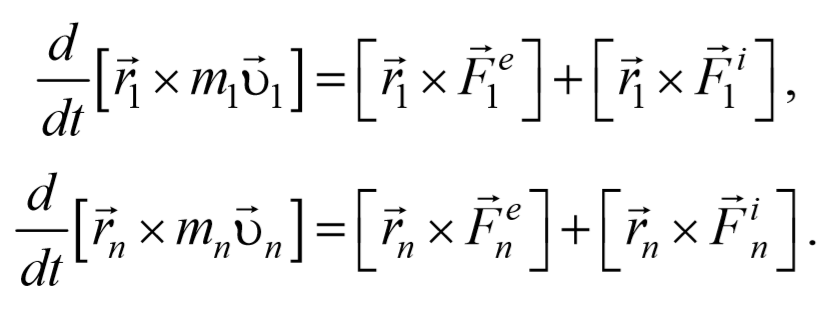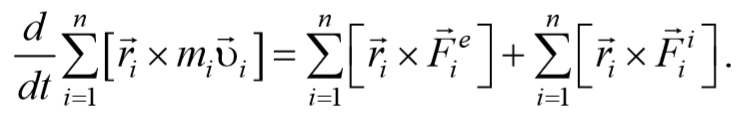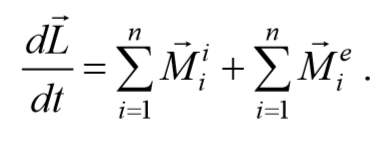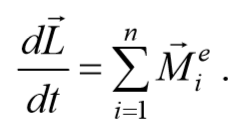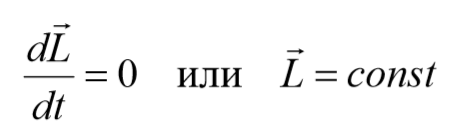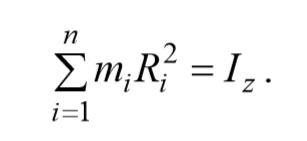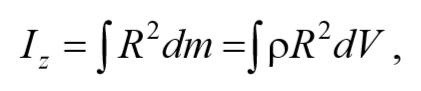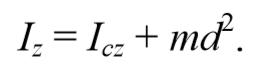Основное уравнение поступательного движения твердого тела

Видео:Поступательное и вращательное движенияСкачать

Техническая механика

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Динамика системы материальных точек

Уравнение поступательного движения твердого тела

Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, — внешними.

Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1) .

Разобьем тело на ряд материальных точек с массами m₁ и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции F_i ин = — m_ia и составим уравнение равновесия:

ΣX = 0 ; F – ΣF_i ин = 0 ,

Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.

Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:

Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.

Уравнение вращательного движения твердого тела

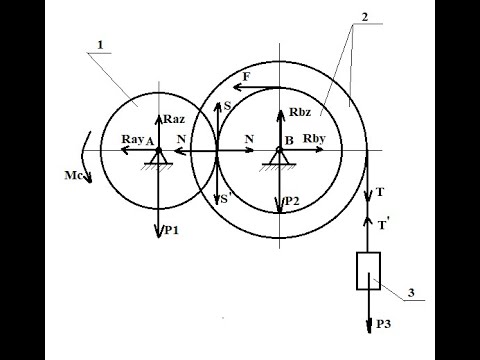
Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2) .

Разобьем тело на ряд материальных точек с массами m_i и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:

Моменты реакций подшипника и подпятника, а также сил F_τi ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом .
Тогда

Выражение Σ(m_ir_i 2 ) называют моментом инерции тела относительно оси и обозначают J :

Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.

В результате получим формулу:

которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.

Единица момента инерции — [J] = [mr 2 ] = [m][r 2 ] = кг×м 2 .

Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.

В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R , толщина s , масса m , относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3) .

Разобьем диск на элементарные кольца переменного радиуса r , шириной dr и толщиной s . Согласно определению момент инерции такого кольца равен

dJ = dΣ(m_ir 2 ) = r 2 dΣm_i = r 2 dm = r 2 2πr drsρ = 2πsρ r 3 dr ,

где ρ – плотность материала диска.

Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:

J = ∫ 2πsρ r 3 dr = 2πsρ ∫ r 3 dr = 2πsρ r 4 /4 = πsρ r 4 /2 .

Так как масса диска m = πr 2 sρ , то можно записать: J = mR 2 /2 .

Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.

Моменты инерции тел вращения

На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле

Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.

Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.

Шар массой m , радиусом R относительно диаметра:

Тонкий стержень массой m , длиной l относительно оси, проходящей перпендикулярно стержню через его конец:

Тонкая сферическая оболочка массой m , радиусом R относительно диаметра:

Пустотелый вал массой m , наружным радиусом R и радиусом отверстия r относительно оси:

Момент инерции Jz тела относительно какой-либо оси z , параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:

Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси , т. е. центральный момент инерции.

Иногда момент инерции определяют по формуле: J = mr_и 2 , где r_и – радиус инерции тела :

Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.

Удвоенный радиус инерции тела называется диаметром инерции : D_и = 2r_и .

В практике иногда вместо момента инерции пользуются понятием махового момента GD_и 2 .

Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.

Единица махового момента — Н×м 2 .

Между маховым моментом и моментом инерции существует простая зависимость:

GD_и 2 = 4g J = 39,24 J .

Кинетическая энергия твердого тела

Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:

Определим выражения для кинетической энергии твердого тела для трех случаев движения.

Тело движется поступательно

Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:

Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.

Тело вращается вокруг неподвижной оси

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

Тело движется плоскопараллельно

Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей) .
Допустим, что известна скорость v_с центра тяжести тела, тогда мгновенная угловая скорость

где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О .

Момент инерции J_о относительно мгновенной оси вращения определяют по формуле:

где J_с — момент инерции относительно центральной оси или центральный момент инерции.

Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:

К_пп = J_оω 2 /2 = (J_с + mОС 2 ) ω 2 /2 = (J_сω 2 )/2 + mOC 2 /2×v_с 2 /ОС 2 ,

Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.

В заключение сформулируем теорему об изменении кинетической энергии системы тел:

Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:

Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.

Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Поступательное движение твердого тела в теоретической механике

Содержание:

Поступательное движение твердого тела:

До сих пор мы изучали движения одной материальной точки. Перейдем теперь к изучению движения твердого тела. Начнем с изучения простого вида движения тела—поступательного, а затем рассмотрим более сложные виды его движений.

Движение тела называется поступательным, если любая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Примерами поступательного движения тела могут служить движение кузова вагона на прямолинейном участке пути, движение поршня внутри цилиндра и пр.

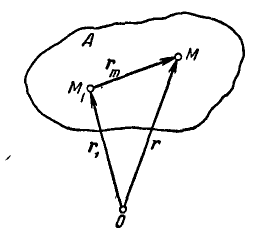
Пусть тело А (рис. 160) движется поступательно.

Возьмем две любые точки твердого тела

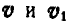
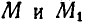
Выразим скорости точек по формуле (72):

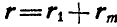
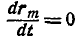
Но так как , то

в силу того, что

Отсюда следует, что при поступательном движении тела все его точки описывают конгруэнтные кривые, имеют равные скорости, а следовательно, и равные ускорения.

Поэтому, изучение поступательного движения тела может быть сведено к изучению движения одной его какой-либо точки. Следовательно, все выводы, полученные при исследовании движения одной точки, могут быть распространены на случай поступательного движения тела.

Задача:

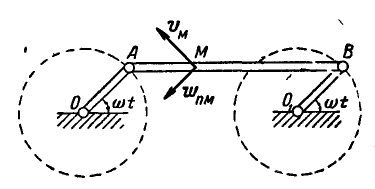
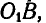
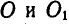
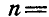
Клавиша соломотряса АВ соединена шарнирно в точках А и В с одинаковыми кривошипами OA и делающими вокруг осей постоянное число оборотов 240 об/мин (рис. 161).

Определить скорость и ускорение любой точки М клавиши, если .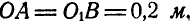

Решение. При равенстве длин кривошипов и одинаковом числе их оборотов клавиша АВ движется поступательно, а поэтому точка М движется тождественно с точками А и В. Скорость и ускорение точки А находим по формулам (89) и (91):

но так как по формуле (94):

Скорость и ускорение точки М, равные скорости и ускорению точки А, показаны на рисунке 161.

Видео:Поступательное и вращательное движения.Скачать

Поступательное движение твердого тела

Поступательным движением называют такое движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному направлению

Поступательное движение тела и его уравнение

Наиболее простым движением твердого тела является поступательное движение. Соединим две какие-либо точки тела отрезком прямой. При поступательном движении тела этот прямолинейный отрезок передвигается параллельно самому себе, не изменяя своего направления. Движение тела называют поступательным, если каждая проведенная в теле прямая сохраняет свое направление.

Для выяснения вопроса, является ли данное движение поступательным, нет необходимости проводить в теле множество прямых и проверять, не меняет ли . каждая из них своего направления во время движения тела. Движение тела вполне определяется движением трех его точек, не лежащих на одной прямой. Следовательно, нужно провести минимум две прямые; конечно, эти прямые должны быть непараллельны между собой.

Из определения видно, что поступательное движение может совершать только тело. Одна точка не может двигаться поступательно. Вместе с тем поступательное движение твердого тела вполне характеризуется движением любой из его точек.

Если тело движется поступательно, то все его точки описывают одинаковые траектории.

Пусть некоторое тело совершает поступательное движение относительно системы координат хОуz (рис. 97, а), которую мы примем за неподвижную и будем называть основной системой отсчета. Отметим в этом теле какую-либо точку Е, движущуюся вместе с телом. Не обращая пока внимания на прочие точки тела, рассмотрим движение точки Е, которое, как движение всякой точки, определяется уравнениями

Давая аргументу t последовательные значения, получим положения точки Е, геометрическое место которых является ее траекторией. На рис. 97 траектория не изображена.

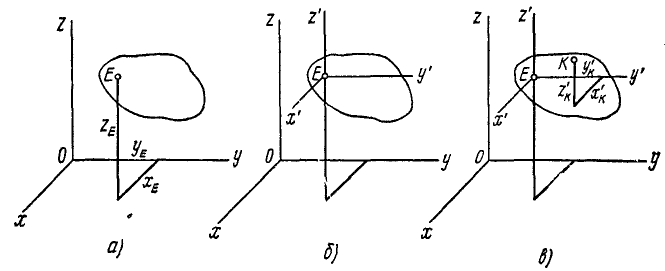
Рис. 97

Проведем теперь в теле через E три взаимно перпендикулярные оси (рис. 97, б), которые назовем подвижной системой отсчета, или подвижными осями координат. Для простоты доказательства в этом параграфе подвижные оси взяты параллельными неподвижным. Подвижные оси передвигаются вместе с телом относительно основных осей, оставаясь им параллельными, по условию поступательного движения.
Отметим в теле какую-либо другую точку К (рис. 97, в), координаты которой относительно подвижных осей обозначим x’κ, y’κ и z’, а относительно основных:

Обратим внимание на то, что координаты x’_K, y’_K и z’_K точки К относительно подвижных осей постоянны, потому что и точка К и подвижные оси взяты в одном и том же твердом теле. Следовательно, при всяком положении поступательно движущегося тела координаты точек E и K отличаются друг от друга на постоянные величины. Отсюда следует, что траектории точек E и К одинаковы и одинаково ориентированы относительно основной системы координат xОyz. Поскольку точки выбраны нами произвольно, доказанное относится к любым точкам тела.

Если определять движение тела по движению его точек, то можно определить поступательное движение тела как движение, при котором перемещения всех точек тела за один и тот же произвольно выбранный промежуток времени равны между собой.

Именно поэтому поступательное движение иногда различают по траекториям, описываемым точками тела. Так, например, говорят, что спарник паровой машины, установленной на фундаменте, совершает круговое поступательное движение; это означает, что все точки спарника описывают одинаковые окружности. Говорят, например, что поршень совершает прямолинейное поступательное движение; это означает, что все точки поршня описывают одинаковые и параллельные прямолинейные траектории.

Задача:

Определить движение спарника тепловоза на прямолинейном участке пути.

Решение. Спарник AB (рис. 98) — это стержень, соединенный шарнирами А и В с кривошипами OA и O1B равной длины. Длина спарника равна расстоянию между осями О и O₁. Такой механизм O₁OAB называют шарнирным параллелограммом. Противоположные звенья его, как противоположные стороны всякого параллелограмма, параллельны между собой: AB ∣∣ OO₁.

При заданном движении тепловоза точки О и O₁ движутся прямолинейно и прямая AB не меняет своего направления, т. е. движется поступательно. (При повороте тепловоза или при изменении уклона железнодорожного пути поступательное движение нарушается.) Все точки спарника описывают одинаковые траектории — укороченные циклоиды.

Ответ. Движение спарника AB поступательное.

Задача:

Круг l радиуса r₁ (рис. 99, а) движется поступательно, постоянно соприкасаясь с неподвижным кругом ll радиуса r₂. Найти траекторию любой точки круга l.

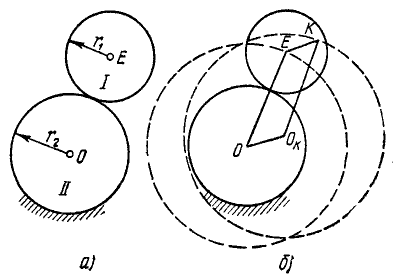
Рис. 99

Решение. Возьмем на подвижном круге l произвольную точку К и соединим с ней центр E подвижного круга отрезком EK (рис. 99, б). От центра О неподвижного круга ll отложим отрезок При поступательном движении круга l отрезок EK, как всякая прямая, проведенная в поступательно движущемся теле, не меняет своего направления и остается равным и параллельным неподвижному отрезку OO_K. Соединив точку О с точкой Е, а точку О_K — с точкой К, получим параллелограмм KE00_K, в котором

Следовательно, при поступательном движении круга l по кругу ll точка К движется, оставаясь на постоянном расстоянии r₁ + r₂ от неподвижной точки О_K, т. е. описывает окружность.

Ответ. Точки круга l описывают окружности радиуса r₁ + r₂.

Задать движение тела — это значит дать положение всех его точек для каждого мгновения. Мы видим, что при поступательном движении твердого тела все его точки движутся одинаково и движение всего тела вполне характеризуется движением какой-либо из его точек. Следовательно, уравнения движения точки E являются одновременно и уравнениями поступательного движения тела.

Часто даже в тех случаях, когда движущееся тело не является твердым, пренебрегают движением некоторых его частей по отношению к другим частям и рассматривают движение системы как по ступательное движение абсолютно твердого тела. Например, движение поезда иногда принимают за поступательное, пренебрегая вращением колес, движениями частей машины и т. п.

Если тело движется поступательно, то все его точки имеют одинаковые скорости

Скорости точек поступательно движущегося тела

Чтобы определить проекции скорости произвольной точки К поступательно движущегося тела на неподвижные оси координат, продифференцируем по времени уравнения (79), помня, что xκ, ук и z’κ постоянны. Найдем

Отсюда следует, что равны и полные скорости (64), и направляющие косинусы (62), иными словами, что равны векторы скоростей точек E и К:
(80 / )

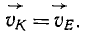
Поскольку эти точки взяты произвольно, доказанное относится к любым точкам тела, а потому во всякое мгновение скорости всех точек поступательно движущегося тела одинаковы.

Одинаковость скоростей не следует понимать как их постоянство, как неизменяемость во времени. Если тело движется поступательно, то в данное мгновение скорости всех точек тела одинаковы; с течением же времени скорости могут измениться. Но если изменится скорость одной точки, то на столько же изменятся скорости всех других точек тела, и они опять-таки останутся одинаковыми.

Одинаковость скоростей всех точек тела — необходимый, но недостаточный признак поступательного движения тела.

Может оказаться, что в какое-либо мгновение скорости всех точек тела одинаковы, но в следующее мгновение они различны. Так, например, движение шатуна AB кривошипно-ползунного механизма не является поступательным, но при некоторых положениях механизма (рис. 100) скорости всех его точек одинаковы.

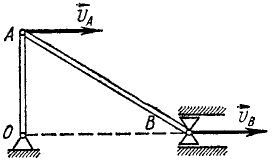
Рис. 100

Если тело движется поступательно, то все его точки имеют одинаковые ускорения

Ускорения точек поступательно движущегося тела

Продифференцировав по времени (80), найдем

откуда следует, что равны векторы ускорений обеих точек:

(81′)

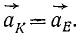
Траектории точек K и E одинаковы и одинаково расположены, а потому к написанным равенствам надо присоединить еще следующие:
a_KT = a_ET и a_KN=a_EN

Во всякое мгновение ускорения всех точек поступательно движущегося тела одинаковы. В этой теореме, как и в предыдущей, одинаковость не надо понимать как неизменяемость с течением времени.

• Вращение твердого тела вокруг неподвижной оси
• Сферическое движение твердого тела
• Плоско-параллельное движение твердого тела
• Движение твердого тела, имеющего неподвижную точку
• Момент силы относительно точки и относительно оси
• Теория пар, не лежащих в одной плоскости
• Произвольная пространственная система сил
• Центр параллельных сил и центр тяжести

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА

4.1. Динамика поступательного движения твердого тела.

Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.

Разобьем твердое тело на элементарные массы m_i , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы

p = $$<sum_^n>$$ m_i υ _i=m υ _C — импульс всех материальных точек твердого тела.

Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс

Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.

4.2. Момент импульса. Момент силы.

Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра

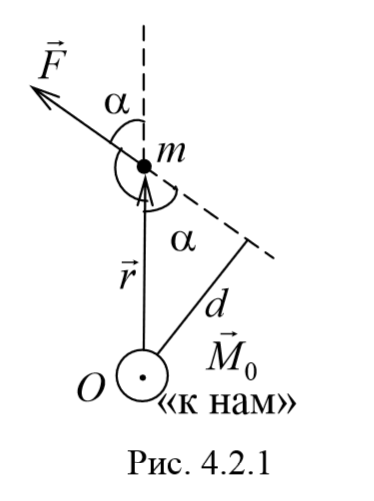
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен

где d=r sin α − плечо силы относительно точки O .

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.

Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:

Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра

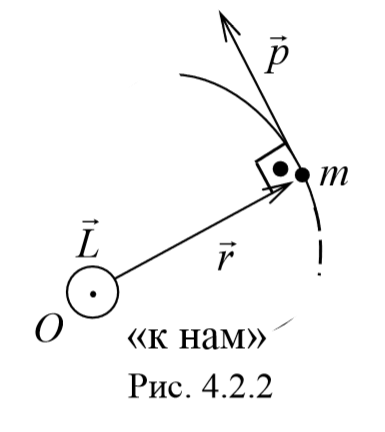
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен

где d − плечо импульса относительно точки O .

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.

Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы

4.3. Основное уравнение динамики вращательного движения относительно точки.

Рассмотрим систему материальных точек массами m₁, m₂, . m_n движущихся со скоростями υ ₁, υ ₂, . υ _n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i ₁, F i ₂, . F i _n , и равнодействующие внешних сил F e ₁, F e ₂, . F e _n .

Запишем уравнения движения частиц:

Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим

Преобразуем данные уравнения

Сложим эти уравнения и получим

В последнем уравнении:

Таким образом, выражение (4.3.6) можно записать в виде

Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<sum_^n>$$ M i _i=0 , получим основное уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы ).

4.4. Закон сохранения момента импульса.

Если момент внешних сил $$<sum_^n>$$ M e _i=0 , то получим

закон сохранения момента импульса.

Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.

Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.

Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.

4.5. Момент инерции.

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .

Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:

где R − расстояние от элементарной массы dm до оси вращения.

4.6. Теорема Штейнера. Правило аддитивности

Существуют два свойства момента инерции:

1) Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

📺 Видео

Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

1 4 Динамика поступательного движенияСкачать

Вращательное движение. 10 класс.Скачать

Лекция 06 Динамика твердого телаСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Простейшие движения твердого телаСкачать

Поступательное и вращательное движение твердого тела. Уравнение движения.Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Простейшие движения твердого телаСкачать

Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Поступательное движение. Вращательное движение твердого телаСкачать

Физика. 10 класс. Основное уравнение динамики вращательного движения /08.10.2020/Скачать