Основное уравнение движения электропривода одномассовой системы для постоянного момента инерции

Воропаев Е.Г.
Электротехника

гл.8 Электропривод и элементы систем автоматикиглава 1| глава 2| глава 3| глава 4| глава 5| глава 6| глава 7| глава 9| глава 10| глава 11|

8.1.ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Oпределение: Электропривод предназначен для приведения в движение различных машин и механизмов. Он состоят из электрического двигателя, аппаратуры управления и передаточных звеньев от двигателя к рабочей машине. Привод бывает групповым, индивидуальным и многодвигательным.

В первом случае один двигатель приводит в движение несколько машин, а во втором каждая машина снабжена своим двигателем.
Многодвигательный привод — это группа двигателей одной машины, где каждый двигатель приводит в движение отдельный механизм.
Из основных требований, предъявляемых к электроприводу, следует отметить следующие:
1. Электродвигатель должен обладать такой мощностью, чтобы он передавал не только статическую нагрузку, но и кратковременные перегрузки.
2. Аппаратура управления должна обеспечить все требования производственного процесса машины, включая регулирование частоты вращения, реверсирование и др.

8.2.УРАВНЕНИЕ ДВИЖЕНИЯ ЭЛЕКТРОПРИВОДА

При работе электропривода вращающий момент электродвигателя должен уравновешивать статический момент сопротивления рабочей машины, а также динамиче-ский момент, обусловленный инерцией движущихся масс. Уравнение моментов электропривода можно записать в виде:

где М — вращающий момент электродвигателя;
М_с — статический момент сопротивления;
М_дин — динамический момент.

Динамический или инерционный момент, как известно из механики, равен:

где j — момент инерции движущихся масс, приведенный к валу двигателя, кг/м 2 ;
w — угловая частота вращения вала двигателя, с -1 .

Выражая угловую частоту вращения w через число оборотов n, получим:

Уравнение моментов электропривода можно записать в другом виде:

Если n = const, то М_дин = 0, тогда М = М_с.

8.3.ВЫБОР МОЩНОСТИ ЭЛЕКТРОДВИГАТЕЛЯ

От правильного выбора мощности электродвигателя зависят технико-экономические показатели электропривода (себестоимость, габариты, экономичность, надежность в эксплуатации и др.).
Если нагрузка на электродвигатель стабильная, то определение его мощности ограничивается лишь выбором по каталогу:

где Р_н — мощность выбираемого двигателя,
Р_нагр — мощность нагрузки.
Если же нагрузка на электродвигатель переменная, то необходимо иметь график нагрузки I = f(t).
Плавную кривую заменяют ступенчатой линией, полагая, что за время t1 в двигателе течет ток I1, за время t2 — ток I2 и. т.д. (рис. 8.3.1 ).

Изменяющийся ток заменяют эквивалентным ему током I_э, который за время одного цикла работы t_ц производит одинаковое, тепловое действие с током, изменяющимся ступенями. Тогда:

а эквивалентный ток
Номинальный ток электродвигателя должен быть равным или больше эквивалентного, т.е.
Поскольку почти у всех двигателей вращающий момент прямо пропорционален току нагрузки М

I_н, то можно записать и выражение для эквивалентного вращающего момента:

Учитывая, что мощность Р = М w , электродвигатель можно выбирать также по эквивалентной мощности:

При повторно-кратковременном режиме двигатель за период работы не успевает нагреться до установившейся температуры, а за время перерыва в работе не охлаждается до температуры окружающей среды (рис. 8.3.2 ).

Для этого режима вводится понятие относительной продолжительности включения (ПВ). Она равна отношению суммы рабочего времени ко времени цикла tц, со-стоящего из времени работы и времени паузы t_о:

Чем больше ПВ, тем меньше номинальная мощность при, равных габаритах. Следовательно, двигатель, рассчитанный на работу в течение 25% времени цикла при номинальной мощности, нельзя оставлять под нагрузкой 60% времени цикла при той же мощности. Электродвигатели строятся для стандартных ПВ — 15, 25, 40, 60%, причем ПВ — 25%; принимается за номинальную. Двигатель рассчитывается на повторно кратковременный режим, если продолжительность цикла не превышает 10 мин. Если расчетные значения ПВ отличаются от стандартных, то при выборе мощности двигателя Рэ следует вносить поправку:

8.4.ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ И ЭЛЕМЕНТЫ

Самым простым и распространенным аппаратом для включения и отключения электрических цепей является рубильник.
Разновидностью рубильника является переключатель, способный перекоммутировать схему, например, при реверсировании или переключении обмоток двигателя со «звезды» на «треугольник».
Рубильник состоит из контактного ножа и двух губок, смонтированных на изолированном основании. Одна из губок является шарнирной. По количеству контактных ножей рубильники бывают одно-, двух- и трёхполюсными. Управление рубильником осуществляется изолированной ручкой, объединяющей контактные ножи.
Иногда при управлении, электродвигателями или другими исполнительными механизмами используются пакетные выключатели. Это малогабаритный отключающий аппарат, как правило, круглой формы (рис. 8.4.1.). В неподвижные кольца 5 из изоляционного материала вмонтированы контакты 3. Внутри колец размещаются подвижные диски 8 с контактными пластинами, закрепленными на оси 7. В крышке 6 помещено пружинное приспособление, с помощью которого достигается быстрое замыкание и размыкание контактов, независимо от скорости поворота ручки 1.
Выключатель собирается и крепится к крышке с помощью скобы 4 и шпилек 2.
Для управления двигателями с фазным ротором требуется большое число переключений, необходимых для ввода или вывода дополнительных сопротивлений.

Эту операцию выполняют контроллеры, которые различают на барабанные и кулачковые (рис. 8.4.2 ).
Подвижные контакты барабанного контроллера, имеющие форму сегментов 4, крепятся на валу 5. Неподвижные контакты 3 размещаются на вертикальной рейке 2 и к ним присоединяются внешние цепи. Контактные сегменты соединяются друг с другом по определенной схеме, и, кроме того, они имеют разную длину дуги.
При повороте вала контроллера сегменты поочередно входят в соприкосновение с неподвижными контактами, и осуществляется включение или отключение цепи.

Вал контроллера снабжается фиксатором 1, обеспечивающим ему несколько фиксированных положений.
Кулачковые контроллеры совершеннее барабанных. На валу 5 крепятся диски фасонного профиля 6, которые воздействуют своей боковой поверхностью на ролик контактного рычага 7, определяя тем самым замкнутое или разомкнутое положение контактов 4 и 3.
Переключения в силовых цепях с помощью контроллеров требует от оператора значительных физических усилий. Поэтому в установках с частыми переключениями для этой цели используются контакторы.
Принцип действия их основан на использовании в управлении силовыми контактами электромагнитной системы. Конструкция контактора приведена на рис. 8.4.3.

На изолированной плите 1 жестко укреплен неподвижный силовой контакт 2. На рычаге 3 шарнирно прикрепленном к плите имеется подвижный силовой контакт 4.
Для управления силовыми контактами на плите смонтирована магнитная система, состоящая из сердечника 5 с катушкой 6 и якоря 7, прикрепленного к рычагу 3. Токоподвод к подвижному контакту осуществляется гибким проводником 8.
При подключении к сети катушки 6 произойдет магнитное притяжение сердечником 5 якоря 7 и замыкание силовых контактов 2 и 4. Для разрыва силовой цепи отключают катушку 6, и якорь под собственным весом отпадает от сердечника.
Помимо силовых контактов, в аппарате имеется ряд блокировочных 9, назначение которых будет показано ниже.
Электрическая цепь катушки электромагнита является вспомогательной или управляющей.
Для управления его применяются кнопки управления. Кнопки бывают одноцепные и двухцепные с замыкающими и размыкающими контактами. В большинстве случаев кнопки делаются с самовозвратом, т.е. при снятии механического давления их контакты возвращаются в исходное положение. На рис. 8.4.4 показана конструкция кнопки с двумя парами контактов: замыкающими и размыкающими.

Для защиты электродвигателя от перегрузки в контактор монтируются два тепловых реле (на две фазы). В этом случае контактор называется магнитным пускателем.
Основной деталью теплового реле (рис. 8.4.5) является биметаллическая пластинка 1, состоящая из двух сплавов с различными коэффициентами расширения.

Пластинка одним концом жестко прикреплена к основанию прибора, а другим упирается в защелку 2, которая под действием пружины 3 стремится повернуться против часовой стрелки. Рядом с биметаллической пластинкой помещается нагреватель 4, включаемый последовательно с двигателем. Когда по силовой цепи потечет большой ток, то температура нагревателя повысится. Биметаллическая пластина прогнется кверху и освободит защелку 2. Под действием пружины 3 защелка поворачивается и через изоляционную пластину 5 размыкает контакты 6 в цепи управления пускателем. Возврат реле возможен только после остывании пластины 1. Он осуществляется нажатием кнопки 7.
Для защиты электроустановок от перегрузок используются также плавкие предохранители. Это неуправляемый аппарат, в котором перегрузка вызывает перегорание плавной вставки, изготовленной из легкоплавкого материала. Предохранители бывает пробчатыми и трубчатыми (рис. 8. 4.6).

Существуют также и управляемые аппараты, защищающие электрооборудование от перегрузок. К ним относится реле максимального тока (рис. 8.4.7 ).
Катушка реле 1 рассчитана на протекание тока в силовой цепи. Для этого она имеет обмотку, изготовленную из провода достаточного поперечного сечения.
При токе, на который настроено реле, произойдет притяжение якоря 2 к сердечнику 3 катушки и с помощью контактного мостика 4 размыкаются контакты 5 в цепи управления магнитного пускателя. Это реле само прервет электроснабжение установки от источника тока.

Нередко встречаются случаи, когда необходимо отключить электроустановку от сети, если уровень напряжения достиг, значения меньше допустимого. Для этой цели используется реле минимального напряжения. Его конструкция напоминает любое электромагнитное реле, но срабатывание здесь происходит при понижении намагниченности катушки и отпадания от нее якоря с контактной системой.
Особое место в схемах защиты электрических установок занимает реле времени. Существуют как электромеханические, так и электронные реле времени.
Рассмотрим конструкцию реле времени типа ЭВ (рис. 8.4.8.).

Основным узлом реле является часовой механизм 2, запускаемый электромагнитной системой 1. Катушка реле включается в силовую цепь и при ее срабатывании часовой механизм вводится в действие. По истечении определенного отрезка времени замкнутся контакты реле и электроустановка отключится от сети. Реле позволяет осуществлять его настройку на различные режимы его работы.
В последние годы получили распространение приборы, в которых электромагнитная и контактная системы объединены в одно целое. Это так называемые герконы (рис. 8.4.9 ).

В герметизированной колбе, заполненной инертным газом, впаяны две или три контактные пластины из пермалоя. Сами контакты (из золота или серебра) находятся на свободных концах пластин. При приближении к геркону постоянного магнита или катушки с током произойдет замыкание или размыкание контактов.
В связи с развитием радиоэлектроники системы автоматического управления пополнились рядом бесконтактных логических элементов. Передачу и преобразование информации от датчика к исполнительному органу можно осуществлять просто, если различать два уровня (две величины) сигнала, каждый из которых может соответствовать, например, символам 0 и 1 или понятиям истинности «да» и «нет». В этом случае сигнал в любой момент времени имеет один из двух возможных значений и называется двоичным сигналом.

8.5.ПРИНЦИПЫ И СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

8.5.1. ПРИНЦИПЫ УПРАВЛЕНИЯ

Принцип автоматического управления заключается в том, что без участия человека осуществляется строгое и последовательное выполнение операций по включению, отключению электрооборудования, а также соблюдение заданного режима его работы.
Различают два вида управления: полуавтоматическое и автоматическое. При полуавтоматическом управлении оператор осуществляет первоначальный пуск объекта (нажатие кнопки, поворот ручки и т.д.). В дальнейшем его функции сводятся лишь к наблюдению за ходом процесса. При автоматическом управлении даже начальный импульс по включению установки посылают датчик или реле. Установка полностью работает в автоматическом режиме по заданной программе.
Программное устройство может быть выполнено как на основе электромеханических элементов, так и с помощью логических схем.

8.5.2. СХЕМЫ УПРАВЛЕНИЯ

Приведем несколько часто встречающихся на практике схем управления электродвигателями.
Самой простой из них является схема управления асинхронным трехфазным двигателем с помощью магнитного искателя.
При нажатии кнопки «пуск» подключается к сети катушка электромагнита. Подвижный якорь придет в соприкосновение с сердечником катушки и своим движением замкнет силовые контакты, подающие трехфазное напряжение на электродвигатель. Одновременно с силовыми, замкнутся и блокировочные контакты, которые зашунти-руют кнопку «пуск», что позволяет ее отпустить. При нажатии кнопки «стоп» разрывается цепь питания катушки электромагнита и якорь, освободившись, отпадает, разомк-нув при этом силовые контакты. Электродвигатель остановится.
Защита электродвигателя от длительной перегрузки здесь обеспечивается двумя тепловыми реле РТ, включенными в две фазы. Отключающие контакты тепловых реле РТ1 и РТ2 введены в цепь питания катушки электромагнита.

Для реверсивного управления двигателем применяется схема с двумя магнитными пускателями (рис. 8.5.2.2.).
Один магнитный пускатель коммутирует схему включения двигателя на прямое вращение, а другой — на обратное.
Кнопки «вперед» и «назад» подключают соответственно свои катушки, а кнопка «стоп» и отключающие контакты теплового реле включены в общую цепь управления.

Основное уравнение движения электропривода

ТИПОВЫЕ РАСЧЕТЫ В ЭЛЕКТРОПРИВОДЕ

Механика электропривода

4.1.1. Приведение статических моментов и моментов инерции к валу двигателя

Механическая часть рабочих органов ( РО ) содержит элементы, вращающиеся с разными скоростями. Передаваемые моменты в связи с этим

также различны. Поэтому необходимо заменить реальную кинематическую

схему РО на расчетную схему, в которой все элементы вращаются со скоростью вала приведения. Чаще всего приведение осуществляют к валу

В задачах требуется по известной кинематической схеме РО составить

расчетную схему, в которой моменты сопротивления движению (статические моменты) и моменты инерции приводятся к валу двигателя. Для этого необходимо изучить кинематическую схему РО, разобраться с принципом работы механической части, выявить основную его технологическую работу и места выделения потерь мощности.

Критерием приведения статических моментов к валу двигателя является энергетический баланс механической части электропривода, обеспечивающий равенство мощностей реальной и расчетной схем электропривода.

Критерием приведения моментов инерции к валу двигателя является равенство запаса кинетической энергии механической части реальной и расчетной схем электропривода.

Критерием приведения жесткости упругой системы к валу двигателя

является равенство запаса потенциальной энергии упругого звена механической части в реальной и расчетной схемах электропривода.

Статические моменты, моменты инерции на валу РО рассчитываются по формулам [5].

Задача 4.1.1

Рассчитать для ПРЯМОГО и ОБРАТНОГО направлений движения значения скоростей, статических моментов и моментов инерции, мощностей

на валу РО и на валу двигателя по заданным технологическим параметрам

механизма подачи (таблица 2.1.1.2, вариант 35).

Технологические данные механизма подачи станка:

Решение

После изучения принципа работы механизма и его кинематической схемы определяем участки выделения потерь:

– в редукторе (потери учитываются кпд η₁₂);

– в передаче « винт – гайка » (потери рассчитываются углом трения φ в нарезке винта);

– в подшипниках ходового винта (потери рассчитываются через коэффициент трения в подшипниках, однако в рассмотренной литературе эти

потери не учитываются).

4.1.1.1. Угловая скорость ходового винта (рабочего органа)

где ρ – радиус приведения передачи « винт – гайка » с шагом h, диаметром

d_ср и углом нарезки резьбы α.

ρ = (d_ср/2)*tg α = (44/2)*tg 5,5° = 2,12 мм.

ω_ро = v/ρ = 42/2,12 = 19,8 рад/с.

4.1.1.2. Момент на валу ходового винта (рабочего органа) с учетом потерь в

передаче «винт – гайка» углом трения φ:

где F_п – суммарное усилие подачи.

= 1,2*6 + ( 2,5*6 + 0,8*6 + 9,81*2,4 )*0,08 = 10,67 кН.

= 10,67*( 0,044/2 )*tg (5,5° + 4° ) = 39,27 Нм.

4.1.1.3. Мощность на валу рабочего органа полезная:

– без учета потерь в передаче « винт – гайка »

– с учетом потерь

4.1.1.4. Статический момент, приведенный к валу двигателя,

4.1.1.5. Угловая скорость вала двигателя

4.1.1.6 Мощность на валу двигателя

Находим элементы кинематической схемы, запасающие кинетическую энергию: суппорт массой m, ходовой винт массой m_хв, шестерни редуктора J1

и J2 , ротор электродвигателя – J_дв.

4.1.1.7. Момент инерции рабочего органа определяется массой m суппорта,

перемещающейся со скоростью v, и моментом инерции ходового винта J_хв.

Момент инерции поступательно движущегося суппорта

J_с = m*v 2 / ω_ро 2 = m*ρ 2 = 2400*0,002122 = 0,0106 кгм 2 .

Момент инерции ходового винта

J_хв = m_хв*( d_ср/2) 2 = 100*( 0,044 /2) 2 = 0,0484 кгм 2 .

Момент инерции рабочего органа

J_ро = J_с + J_хв = 0,0106 + 0,0484 = 0,059 кгм 2 .

4.1.1.8. Момент инерции рабочего органа, приведенный к валу двигателя,

J_пр = J_ро / i₁₂ 2 = 0,059 / 52 =0,00236 кгм 2 .

4.1.1.9. Момент инерции передачи, приведенный к валу двигателя,

J_пер = J1 + J2 / i₁₂ 2 = 0,03 + 0,6 / 52 = 0,054 кгм 2 .

4.1.1.10. Коэффициент, учитывающий момент инерции передачи в моменте

инерции ротора двигателя,

4.1.1.11.Суммарный момент инерции механической части электропривода

J = δ*J_дв + J_пр = 1,27*0,2 + 0,00236 = 0,256 кгм 2 .

Основное уравнение движения электропривода

При переменных статических моментах и моментах инерции, зависящих от скорости, времени, угла поворота вала двигателя ( линейного перемещения РО ), уравнение движения электропривода записывается в общем виде:

М( х ) – М_с ( х ) = J(х)*dω / dt + (ω/2)*dJ(x)/ dt.

При постоянном моменте инерции J = const уравнение упрощается

М(х) – М_с (х) = J*dω / dt, и его называют основным уравнением движения.

Правую часть уравнения М(х) – М_с (х) = М_дин называют динамическим

моментом. Знак М_дин определяет знак производной dω/dt и состояние электропривода:

– М_дин = dω / dt > 0 – двигатель разгоняется;

– М_дин = dω / dt

где T_д= J * ω_он / М_н – механическая постоянная времени электропривода, учитывающая и приведенный момент инерции РО. Наличие в уравнении Т_д

свидетельствует о записи уравнения в о.е.

Задача 4.1.2.1

Рассчитать для механизма с двигателем ( Р_н =8,1 кВт, ω_н = 90 рад/с, U_н = 100 В, I_н = 100 А ) и суммарным моментом инерции J = 1 кгм 2 динамический момент М_дин, ускорение электропривода ε, конечное значение скорости ω_кон, угол поворота вала двигателя α за промежуток времени Δt = t_i / T_д = 0,5, если М = 1,5, М_с = 0,5, ω_нач =0,2.

Решение

Основное уравнение движения в о.е.

Механическая постоянная времени двигателя

Значения ω_он и М_н рассчитаем по каталожным данным двигателя (см. задачу 4.2.1 ).

Скорость идеального холостого хода

Номинальный электромагнитный момент

Механическая постоянная времени

4.1.2.1. Динамический момент

4.1.2.2. Ускорение электропривода ( при t_б = Т_д )

Приращение скорости за промежуток времени Δt = t_i / T_д = 0,5:

4.1.2.3. Конечное значение скорости на участке

4.1.2.4. Приращение угла поворота

= 0,2 * 0,5 +( 0,7 + 0,2)*0,5 / 2 = 0,325.

Определим полученные значения в абсолютных единицах:

ε = ε* ω_он / t_б= 1 * 100 / 1 = 100 рад / с 2 ;

Δω = Δω* ω_он = 0,5* 100 = 50 рад / с;

Δα = Δα * ω_он *t_б = 0,325*100 *1 = 32,5 рад.

4.1.3. Переходные процессы механической части электропривода

Для расчета и построения нагрузочных диаграмм М(t) и ω(t) используется решение основного уравнения движения

из которого для конечных приращений при М = const и М_c = const для заданного t_i получим приращение скорости

и значение скорости в конце участка

Задача 4.1.3.1

Для двигателя ( ω_он=100 рад/с, M_н=100 Нм, J=1кгм 2 ) рассчитать ускорение и построить переходный процесс ω(t), если М = 2, ω_нач = 0, М_с = 0.

Решение

Механическая постоянная времени

и при t_i = Т_д получаем Δω = 2.

Скорость за это время достигнет значения

ω = ω_нач + Δω = 0+2 = 2.

Значения ω = 1 скорость достигнет за Δt = 0,5, в этот момент времени разгон прекращают, снижая момент двигателя до величины статического момента М = М_с ( см. рис. 4.1.3.1).

Рис. 4.1.3.1. Механический переходный процесс при М=const

Задача 4.1.3.2

Для двигателя (ω_он=100 рад/с, M_н=100 Нм, J=1кгм 2 ) рассчитать ускорение и построить переходный процесс реверса ω(t), если М = – 2, ω_нач =

Решение

За базовое время t_б=Т_д приращение скорости Δω = –3, конечная скорость

Двигатель остановится (ω_кон = 0) при Δω = – 1 за время t_i = Т_д / 3. Реверс закончится при ω_кон = – 1, при этом Δω = –2, t_i = 2* Т_д/3. В этот момент времени следует снизить момент двигателя до М = М_с. Рассмотренный переходный процесс справедлив для активного статического момента (см.

При реактивном статическом моменте, который изменяет свой знак при изменении направления движения, переходный процесс распадается на два

этапа. До остановки двигателя переходный процесс протекает также, как и при активном М_с. Двигатель остановится, ω_кон = 0, тогда Δω = – 1, время торможения t_i = Т_д / 3.

При изменении направления движения меняются начальные условия:

М_с = – 1; ω_нач = 0; М = – 2, начальное время Δt_нач = Т_д/3.

Тогда приращение скорости составит

При t_i =Т_д приращение скорости Δω = – 1, ω_кон = –1, разгон в обратную сторону произойдет за Δt = Т_д , реверс закончится за Δt = 4*Т_д/3. В этот момент времени следует снизить момент двигателя до М = М_с ( см. рис. 4.1.3.2,б). Таким образом, при реактивном М_с время реверса увеличилось

Уравнение движения электропривода. Динамика механической части ЭП

Динамика механической части ЭП

Уравнение движения электропривода

В соответствии с законом Ньютона поступательное движение в системе ЭП описывается, как F – F_c = F_дин=m·dV/dt, (3.1)

где F — движущая сила, F_c — сила сопротивления, F_дин — инерционная сила.

Для вращательного движения это уравнение имеет аналогичный вид

Здесь аналогом массы является суммарный приведенный к валу двигателя момент инерции J , вместо линейной скорости V рассматривается угловая скорость двигателя w, а в левую часть уравнения входят момент двигателя Ми статический момент сопротивления механизма М_с. Динамический момент М_дин, равный разности движущего и момента сопротивления, пропорционален угловому ускорению электропривода.

Уравнение (3.2) в электроприводе получило название «уравнение движения», по которому динамический момент возникает только в переходных режимах, т. е. тогда, когда меняется кинетическая энергия при ускорении и замедлении электропривода. Приведенные уравнения (3.1) и (3.2) можно применять лишь для электроприводов с J=const.

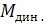
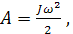
В общем случае выражение для определения динамического момента можно определить из уравнения запаса кинетической энергии для вращающегося тела:

(3.3)

где J = m· r 2 – момент инерции тела, обладающего массой m ;

r – радиус вращающегося тела правильной цилиндрической формы.

Мощность, которую вращающиеся массы получают при ускорении электропривода или отдают при торможении:

(3.4)

Тогда, динамический момент можно найти с учетом :

. (3.5)

Уравнение для определения динамического момента состоит из двух составляющих: первое из них определяет изменение динамического момента при изменении угловой скорости ω электропривода, второе — при изменении его момента инерции во времени или угла поворота α вращающегося рабочего механизма.

У поступательно движущегося рабочего механизма со скоростью V и массой m динамическая составляющая мощности определяется из запаса кинетической энергии:

(3.6)

Динамическое усилие на рабочем органе определяется:

, (3.7)

где динамическое усилие определяется ускорением поступательно движущегося рабочего органа и изменением массы при движении рабочего органа.

В качестве примеров изменения момента инерции в уравнении (3.5) можно привести зависимость момента инерции барабана с многослойной навивкой каната подъемной установки от глубины подъема, изменение момента инерции кабельного барабана в установках кабельного производства. Примером изменения массы при поступательном движении рабочего механизма является изменение массы ковша при черпании грунта экскаватором — драглайном, изменение массы груза ленточного конвейера.

Рассмотренные выше условия изменения в уравнениях движения электропривода возникают при работе машин, в которых перемещение рабочего органа по пространственным траекториям осуществляется несколькими индивидуальными электроприводами, предусмотренными для каждой координаты перемещения (экскаваторы, краны, роботы и т.п.).

В подобных случаях приведенный момент инерции электропривода, как и статический момент сопротивления, следует полагать независимой функцией времени J(t). Тогда уравнение движения электропривода примет вид:

(3.8)

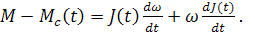
Функции J(t) и M_c(t) при этом следует определить путем анализа движения электропривода, вызывающего изменения момента инерции и нагрузки.

Полученные математические описания динамических процессов в механической части электропривода, представляемой уравнениями движения, позволяют анализировать возможные режимы движения электропривода. Условием динамического процесса в системе, описываемой (3.8), является dw/dt¹0, т.е. наличие изменений скорости электропривода.

Для анализа статических режимов работы электропривода необходимо положить dw/dt=0.

💥 Видео