Классический метод анализа переходных колебаний в Электрических Цепях
При выполнении задачи анализа переходных колебаний в ЭЦ классическим методом рекомендуется следующая последовательность действий:
• рассчитываются начальные условия задачи;
• составляется система уравнений с использованием законов Кирхгофа;
• выбирается переменная uC или iL,формируется дифференциальное уравнение с этой переменной соответствующего порядка и записывается его решение;
• рассчитывается вынужденная составляющая (при t ® ¥) для выбранной переменной;
• рассчитывается свободная составляющая для выбранной переменной.
1.1. Анализ переходных колебаний в разветвленных RC-цепях
путем составления дифференциального уравнения
[1, с. 185–187; 2, с. 157–167]
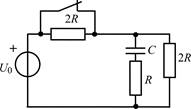 |
| Рис. 1.1 |
1.1.0. Найдите законы изменения напряжения uC(t) на емкости и тока iC(t) через емкость в цепи на рис. 1.1 после размыкания ключа. Постройте примерные графики.
Во всех задачах анализа переходных колебаний предполагается, что до коммутации в цепи был установившийся режим, и положение ключа на схеме цепи показано до коммутации.
В задачах 1.1.1–1.1.25 найдите законы изменения напряжения uC(t) на емкости и тока iC(t) через емкость после коммутации. Постройте примерные графики.
Таблица 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.1 | 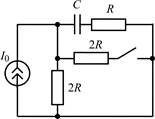 | 1.1.2 | 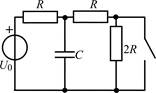 |
| 1.1.3 | 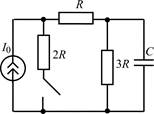 | 1.1.4 | 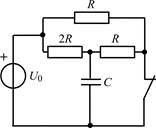 |
| 1.1.5 | 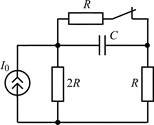 | 1.1.6 | 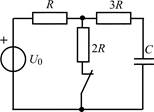 |
| 1.1.7 | 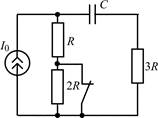 | 1.1.8 |  |
| 1.1.9 | 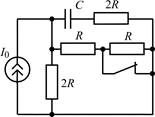 | 1.1.10 | 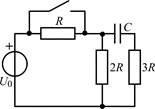 |
Продолжение табл. 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.11 |  | 1.1.12 | 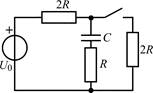 |
| 1.1.13 | 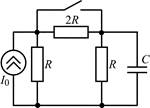 | 1.1.14 | 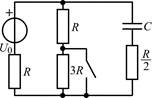 |
| 1.1.15 | 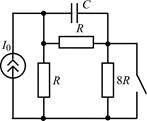 | 1.1.16 | 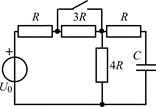 |
| 1.1.17 | 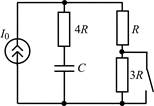 | 1.1.18 | 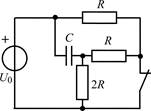 |
| 1.1.19 |  | 1.1.20 |  |
Окончание табл. 1.1
| Вариант | Схема RC-цепи | Вариант | Схема RC-цепи |
| 1.1.21 | 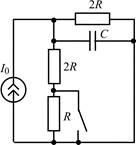 | 1.1.22 | 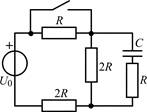 |
| 1.1.23 | 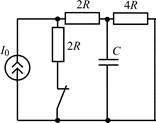 | 1.1.24 |  |
| 1.1.25 | 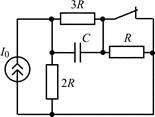 |
1.2. Анализ переходных колебаний в разветвленных RL-цепях
путем составления дифференциального уравнения
[1, с. 185–197; 2, с. 157–167]
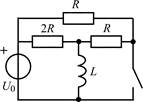 |
| Рис. 1.2 |
1.2.0. Найдите закон изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности в цепи на рис. 1.2 после замыкания ключа. Постройте примерные графики.
В задачах 1.2.1–1.2.25 найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи |
| 1.2.1 | 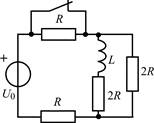 | 1.2.2 | 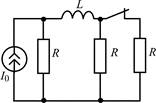 |
| 1.2.3 | 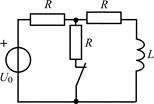 | 1.2.4 | 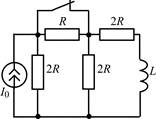 |
| 1.2.5 | 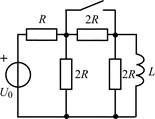 | 1.2.6 |  |
| 1.2.7 | 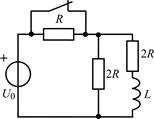 | 1.2.8 | 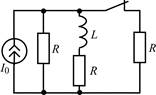 |
Продолжение табл. 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи |
| 1.2.9 | 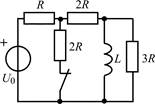 | 1.2.10 | 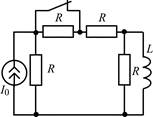 |
| 1.2.11 |  | 1.2.12 |  |
| 1.2.13 | 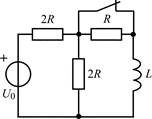 | 1.2.14 | 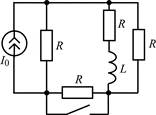 |
| 1.2.15 | 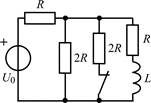 | 1.2.16 | 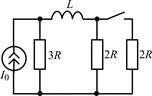 |
| 1.2.17 | 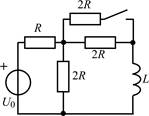 | 1.2.18 | 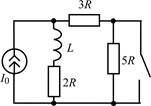 |
Окончание табл. 1.2
| Вариант | Схема RL-цепи | Вариант | Схема RL-цепи |
| 1.2.19 | 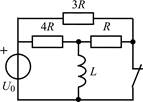 | 1.2.20 | 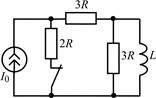 |
| 1.2.21 | 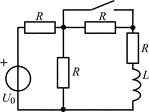 | 1.2.22 | 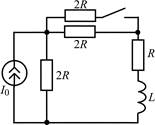 |
| 1.2.23 | 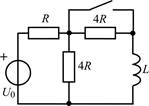 | 1.2.24 | 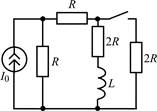 |
| 1.2.25 | 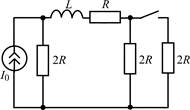 |
1.3. Анализ разветвленной цепи с одним реактивным элементом
с использованием формулы 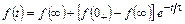
[1, с. 197–198]
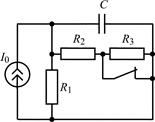 |
| Рис. 1.3 |
1.3.0. Найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость в цепи на рис. 1.3 после размыкания ключа, если I0 = 1 А; R1 = R2 = 36 Ом; R3 = 144 Ом; С = 0,1 мкФ. Постройте примерные графики.
В задачах 1.3.1–1.3.25 в RC-цепяхнайдите законы изменения напряжения uС(t) на емкости и тока iС(t) через емкость, в RL-цепях найдите законы изменениятока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.1 | 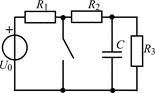 U0 = 25 В; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 0,5 мкФ U0 = 25 В; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 0,5 мкФ | 1.3.2 |  I0 = 5 мА; R1 = 2 кОм; R2 = 3 кОм; R3 = 5 кОм; С = 0,1 мкФ I0 = 5 мА; R1 = 2 кОм; R2 = 3 кОм; R3 = 5 кОм; С = 0,1 мкФ |
| 1.3.3 | 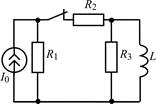 I0 = 8 мА; R1 = R2 = 5 кОм; R3 = 4 кОм; L = 0,8 Гн I0 = 8 мА; R1 = R2 = 5 кОм; R3 = 4 кОм; L = 0,8 Гн | 1.3.4 |  U0 = 40 В; R1 = 15 кОм; R2 = R3 = 10 кОм; L = 0,5 Гн U0 = 40 В; R1 = 15 кОм; R2 = R3 = 10 кОм; L = 0,5 Гн |
Продолжение табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.5 | 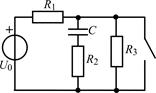 U0 = 10 В; R1 = 2 кОм; R2 = 4 кОм; R3 = 8 кОм; С = 0,25 мкФ U0 = 10 В; R1 = 2 кОм; R2 = 4 кОм; R3 = 8 кОм; С = 0,25 мкФ | 1.3.6 |  I0 = 5 мА; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 5000 пФ I0 = 5 мА; R1 = 2 кОм; R2 = R3 = 4 кОм; С = 5000 пФ |
| 1.3.7 | 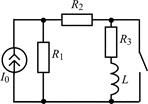 I0 = 10 мА; R1 = R3 = 1 кОм; R2 = 3 кОм; L = 20 мГн I0 = 10 мА; R1 = R3 = 1 кОм; R2 = 3 кОм; L = 20 мГн | 1.3.8 | 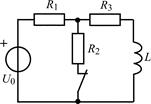 U0 = 12 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 12 мГн U0 = 12 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 12 мГн |
| 1.3.9 | 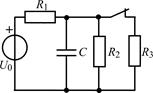 U0 = 60 В; R1 = 4 кОм; R2 = R3 = 2 кОм; С = 0,3 мкФ U0 = 60 В; R1 = 4 кОм; R2 = R3 = 2 кОм; С = 0,3 мкФ | 1.3.10 | 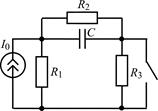 I0 = 8 мА;R1 = R2 = 10 кОм; R3 = 20 кОм; С = 0,2 мкФ I0 = 8 мА;R1 = R2 = 10 кОм; R3 = 20 кОм; С = 0,2 мкФ |
| 1.3.11 | 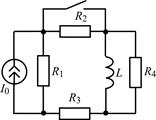 I0 = 15 мА; R1 = 100 Ом; R2 = R3 = 200 Ом; R4 = 300 Ом; L = 0,15 Гн I0 = 15 мА; R1 = 100 Ом; R2 = R3 = 200 Ом; R4 = 300 Ом; L = 0,15 Гн | 1.3.12 | 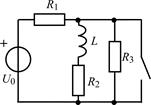 U0 = 20 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 4 мГн U0 = 20 В; R1 = 1 кОм; R2 = R3 = 2 кОм; L = 4 мГн |
Продолжение табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.13 | 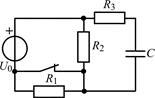 U0 = 24 В; R1 = R2 = 4 кОм; R3 = 3 кОм; С = 0,2 мкФ U0 = 24 В; R1 = R2 = 4 кОм; R3 = 3 кОм; С = 0,2 мкФ | 1.3.14 | 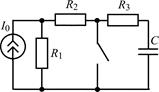 I0 = 4 мА; R1 = 5 кОм; R2 = 3 кОм; R3 = 2 кОм; С = 0,5 мкФ I0 = 4 мА; R1 = 5 кОм; R2 = 3 кОм; R3 = 2 кОм; С = 0,5 мкФ |
| 1.3.15 | 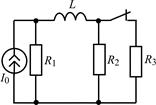 I0 = 6 мА; R1 = R2 = R3 = 2 кОм; L = 40 мГн I0 = 6 мА; R1 = R2 = R3 = 2 кОм; L = 40 мГн | 1.3.16 | 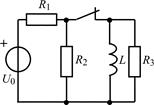 U0 = 30 В; R1 = 2 кОм; R2 = R3 = 6 кОм; L = 6 мГн U0 = 30 В; R1 = 2 кОм; R2 = R3 = 6 кОм; L = 6 мГн |
| 1.3.17 |  U0 = 36 В; R1 = R2 = R4 = 2 кОм; R3 = 1 кОм; С = 0,5 мкФ U0 = 36 В; R1 = R2 = R4 = 2 кОм; R3 = 1 кОм; С = 0,5 мкФ | 1.3.18 | 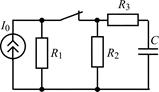 I0 = 10 мА; R1 = R2 = 2 кОм; R3 = 3 кОм; С = 0,4 мкФ I0 = 10 мА; R1 = R2 = 2 кОм; R3 = 3 кОм; С = 0,4 мкФ |
| 1.3.19 | 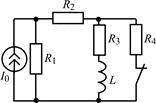 I0 = 20 мА; R2 = 1 кОм; R1 = R3 = R4 = 2 кОм; L = 50 мГн I0 = 20 мА; R2 = 1 кОм; R1 = R3 = R4 = 2 кОм; L = 50 мГн | 1.3.20 | 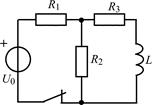 U0 = 40 В; R1 = 240 Ом; R2 = 800 Ом; R3 = 200 Ом; L = 0,2 Гн U0 = 40 В; R1 = 240 Ом; R2 = 800 Ом; R3 = 200 Ом; L = 0,2 Гн |
Окончание табл. 1.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.3.21 | 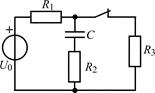 U0 = 24 В;R1 = 2 кОм; R2 = 3 кОм; R3 = 4 кОм; С = 0,2 мкФ U0 = 24 В;R1 = 2 кОм; R2 = 3 кОм; R3 = 4 кОм; С = 0,2 мкФ | 1.3.22 | 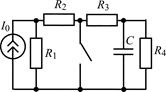 I0 = 20 мА; R1 = 3 кОм; R2 = R3 = R4 = 1 кОм; С = 0,2 мкФ I0 = 20 мА; R1 = 3 кОм; R2 = R3 = R4 = 1 кОм; С = 0,2 мкФ |
| 1.3.23 | 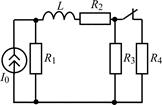 I0 = 36 мА; R1 = 4 кОм; R2 = 3 кОм; R3 = R4 = 2 кОм; L = 18 мГн I0 = 36 мА; R1 = 4 кОм; R2 = 3 кОм; R3 = R4 = 2 кОм; L = 18 мГн | 1.3.24 | 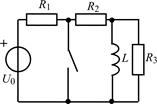 U0 = 25 В; R1 = 300 Ом; R2 = 200 Ом; R3 = 800 Ом; L = 0,16 Гн U0 = 25 В; R1 = 300 Ом; R2 = 200 Ом; R3 = 800 Ом; L = 0,16 Гн |
| 1.3.25 | 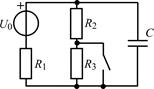 | U0 = 6 В; R1 = R2 = 2 кОм; R3 = 8 кОм; С = 0,5 мкФ |
1.4. Анализ свободных (переходных) колебаний
при отключении (подключении) к цепи
источника гармонических колебаний
[1, с. 185–198; 2, с. 157–167]
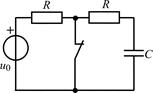 |
| Рис. 1.4 |
1.4.0. Найдите закон изменения напряжения uC(t) на емкости в цепи на рис. 1.4 после размыкания ключа, если u0(t) = 5cos10 6 t В, R = 500 Ом, С = 1000 пФ. Постройте примерный график.
В задачах 1.4.1–1.4.6 найдите закон изменения тока iL(t) в индуктивности после коммутации. Постройте примерные графики.
Таблица 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.1 |  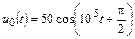 , В; R = 5 кОм; L = 50 мГн , В; R = 5 кОм; L = 50 мГн | 1.4.2 | 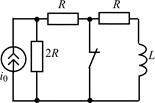 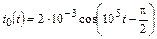 , А; R = 1 кОм; L = 40 мГн , А; R = 1 кОм; L = 40 мГн |
| 1.4.3 | 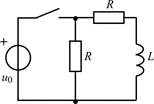 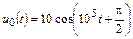 , В; R = 2 кОм; L = 20 мГн , В; R = 2 кОм; L = 20 мГн | 1.4.4 |   , А; R = 0,5 кОм; L = 10 мГн , А; R = 0,5 кОм; L = 10 мГн |
| 1.4.5 | 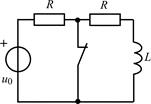 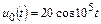 , В; R = 1 кОм; L = 20 мГн , В; R = 1 кОм; L = 20 мГн | 1.4.6 | 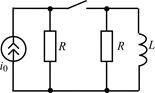 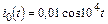 , А; R = 0,3 кОм; L = 15 мГн , А; R = 0,3 кОм; L = 15 мГн |
В задачах 1.4.7–1.4.13 найдите закон изменения напряжения uC(t) на емкости после коммутации. Постройте примерные графики.
Продолжение табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.7 | 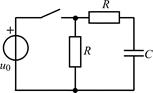 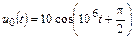 , В; R = 2 кОм; C = 500 пФ , В; R = 2 кОм; C = 500 пФ | 1.4.8 |   , В; R = 1 кОм; C = 1000 пФ , В; R = 1 кОм; C = 1000 пФ |
| 1.4.9 | 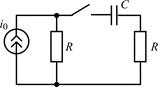 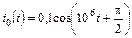 , А; R = 40 Ом; С = 0,0125 мкФ , А; R = 40 Ом; С = 0,0125 мкФ | 1.4.10 | 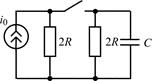 i0 = 0,05cos10 7 t, А; R = 1 кОм; C = 100 пФ i0 = 0,05cos10 7 t, А; R = 1 кОм; C = 100 пФ |
| 1.4.11 | 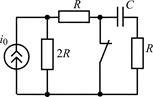 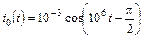 , А; R = 500 Ом; С = 500 пФ , А; R = 500 Ом; С = 500 пФ | 1.4.12 | 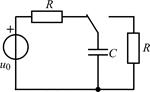 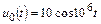 , В; R = 1 кОм; C = 1000 пФ , В; R = 1 кОм; C = 1000 пФ |
| 1.4.13 | 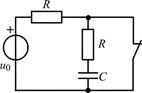 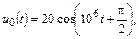 В; R = 500 Ом; C = 1000 пФ В; R = 500 Ом; C = 1000 пФ |
В задачах 1.4.14–1.4.19 найдите закон изменения напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.14 | 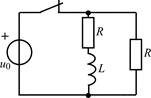 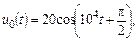 В; R = 500 Ом; L = 50 мГн В; R = 500 Ом; L = 50 мГн | 1.4.15 |  u0(t) = 20cos10 5 t В; R = 500 Ом; L = 10 мГн u0(t) = 20cos10 5 t В; R = 500 Ом; L = 10 мГн |
| 1.4.16 | 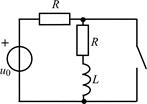 u0(t) = 10cos10 5 t , В; R = 1 кОм; L = 20 мГн u0(t) = 10cos10 5 t , В; R = 1 кОм; L = 20 мГн | 1.4.17 | 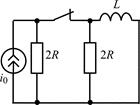 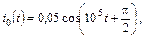 А; R = 5 кОм; L = 50 мГн А; R = 5 кОм; L = 50 мГн |
| 1.4.18 | 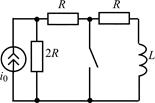 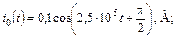 R = 2,5 кОм; L = 40 мГн R = 2,5 кОм; L = 40 мГн | 1.4.19 | 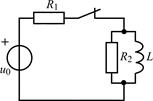  R1 = 10 Ом; R2 = 60 Ом; L = 10 мГн R1 = 10 Ом; R2 = 60 Ом; L = 10 мГн |
В задачах 1.4.20–1.4.25 найдите закон изменения тока iC(t) через емкость после коммутации. Постройте примерные графики.
Окончание табл. 1.4
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.4.20 | 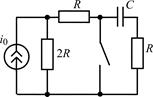 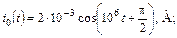 R = 1 кОм; С = 250 пФ R = 1 кОм; С = 250 пФ | 1.4.21 | 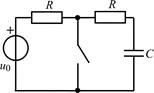 u0 = 8cos10 6 t , В; R = 2 кОм; С = 250 пФ u0 = 8cos10 6 t , В; R = 2 кОм; С = 250 пФ |
| 1.4.22 | 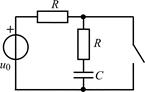 u0(t) = 20cos10 7 t, В; R = 200 Ом; С = 250 пФ u0(t) = 20cos10 7 t, В; R = 200 Ом; С = 250 пФ | 1.4.23 | 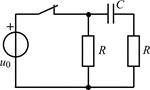 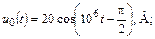 R = 2 кОм; С = 500 пФ R = 2 кОм; С = 500 пФ |
| 1.4.24 | 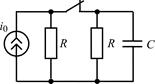 i0(t) = 0,01cos4×10 4 t , А; R = 10 кОм; С = 5000 пФ i0(t) = 0,01cos4×10 4 t , А; R = 10 кОм; С = 5000 пФ | 1.4.25 |  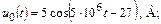 R1 = 0,5 кОм; R2 = 1 кОм; С = 2000 пФ R1 = 0,5 кОм; R2 = 1 кОм; С = 2000 пФ |
1.5. Составление уравнений переменных состояния цепи
[1, с. 89–93, 211–218; 2, с. 178–183]
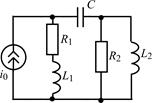 |
| Рис. 1.5 |
1.5.0. Составьте систему линейных дифференциальных уравнений по методу переменных состояния в нормальной форме для цепи на рис. 1.5, используя законы Кирхгофа. Запишите полученную систему уравнений состояния цепи в матричной форме.
В задачах 1.5.1–1.5.25 составьте систему линейных дифференциальных уравнений по методу переменных состояния в нормальной форме, используя законы Кирхгофа. Запишите полученную систему уравнений состояния цепи в матричной форме.
Таблица 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.1 | 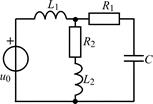 | 1.5.2 | 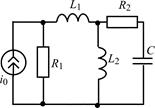 |
| 1.5.3 | 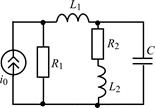 | 1.5.4 | 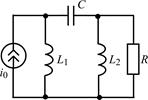 |
| 1.5.5 | 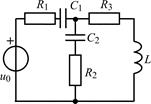 | 1.5.6 | 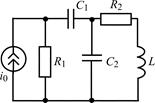 |
Продолжение табл. 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.7 | 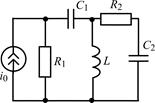 | 1.5.8 | 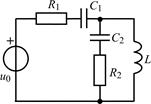 |
| 1.5.9 | 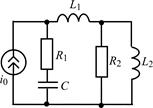 | 1.5.10 | 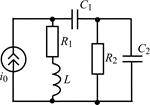 |
| 1.5.11 | 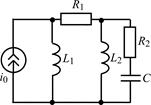 | 1.5.12 |  |
| 1.5.13 | 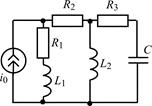 | 1.5.14 | 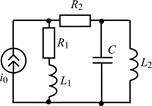 |
| 1.5.15 |  | 1.5.16 | 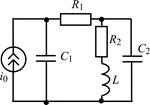 |
Окончание табл. 1.5
| Вариант | Схема цепи | Вариант | Схема цепи |
| 1.5.17 | 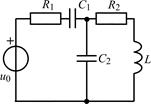 | 1.5.18 | 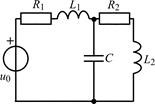 |
| 1.5.19 | 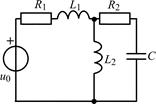 | 1.5.20 | 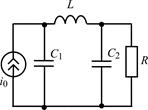 |
| 1.5.21 | 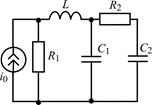 | 1.5.22 | 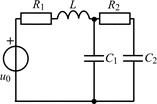 |
| 1.5.23 | 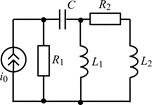 | 1.5.24 | 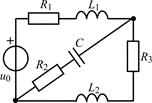 |
| 1.5.25 | 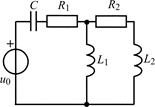 |
Контрольные вопросы
1. Что такое переходный процесс? В каких схемах он возникает и почему?
2. Что называют начальными условиями задачи?
3. Сформулируйте законы коммутации. Каков их физический смысл? Как они были использованы при решении задач?
4. От чего зависит порядок дифференциального уравнения цепи?
5. Когда режим в цепи называется свободным, когда вынужденным?
6. Чем отличаются дифференциальные уравнения, описывающие свободные и переходные колебания в цепи? Чем отличаются их решения?
7. Как находится характеристическое уравнение цепи по заданному дифференциальному уравнению?
8. Что называют постоянной времени цепи? Как от нее зависит длительность переходного процесса?
9. Как определяются постоянные времени RC— и RL-цепей?
10. Как определяются и от чего зависят собственные (свободные) колебания в цепи?
11. Как определяются и от чего зависят вынужденные колебания в цепи?
12. Что называют переменными состояния цепи?
13. Как составляются уравнения состояния цепи? Чем определяется порядок системы уравнений состояния цепи?
14. Запишите уравнения переменных состояния цепи в нормальной форме.
Операторный метод анализа переходных колебаний в Электрических Цепях
При выполнении задачи анализа переходных колебаний в ЭЦ операторным методом рекомендуется следующая последовательность действий:
• рассчитываются начальные условия задачи;
• составляется операторная схема замещения цепи, в которой ненулевые начальные условия учитываются введением дополнительных источников (рис. П2.1);
• определяется L-изображение искомого тока или напряжения любым из ранее изученных методов расчета цепей: методом эквивалентных преобразований, методом узловых напряжений, методом эквивалентного генератора;
• определяется мгновенное значение искомого тока или напряжения по таблице соответствия функций времени и их изображений (табл. П2.1) или по теореме разложения.
2.1. Анализ переходных колебаний в RC— и RL-цепях
при нулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
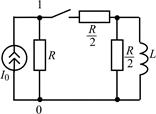 |
| Рис. 2.1 |
2.1.0. Найдите закон изменения напряжения u10(t) на зажимах генератора в цепи на рис. 2.1 после замыкания ключа. Постройте примерный график.
В задачах 2.1.1–2.1.4 найдите закон изменения напряжения uC(t) на емкости после коммутации. Постройте примерные графики.
Таблица 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.1 | 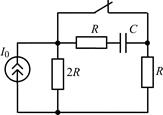 | 2.1.2 | 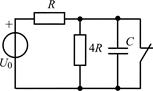 |
| 2.1.3 | 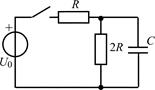 | 2.1.4 | 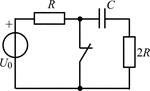 |
В задачах 2.1.5–2.1.10 найдите закон изменения тока iC(t) через емкость после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.5 | 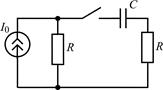 | 2.1.6 | 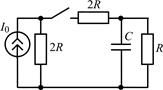 |
| 2.1.7 | 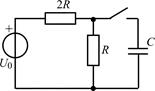 | 2.1.8 | 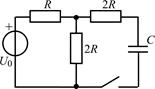 |
| 2.1.9 | 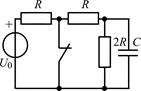 | 2.1.10 | 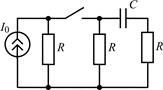 |
В задачах 2.1.11–2.1.16 найдите закон изменения тока iL(t) в индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.11 | 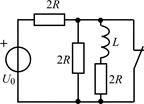 | 2.1.12 |  |
| 2.1.13 | 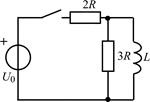 | 2.1.14 | 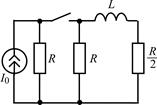 |
| 2.1.15 | 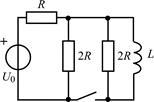 | 2.1.16 | 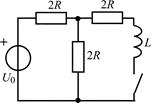 |
В задачах 2.1.17–2.1.22 найдите закон изменения напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Продолжение табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.17 | 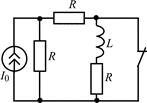 | 2.1.18 | 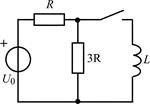 |
| 2.1.19 | 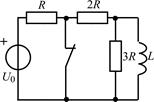 | 2.1.20 | 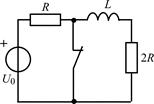 |
| 2.1.21 |  | 2.1.22 | 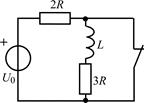 |
В задачах 2.1.23–2.1.25 найдите закон изменения тока i(t) после коммутации. Постройте примерные графики.
Окончание табл. 2.1
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.1.23 | 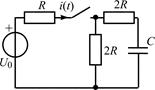 | 2.1.24 | 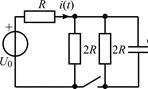 |
| 2.1.25 | 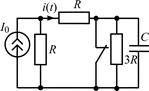 |
2.2. Анализ переходных колебаний в RC-цепях
при ненулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
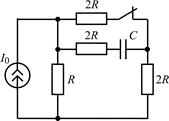 |
| Рис. 2.2 |
2.2.0. Найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость в цепи на рис. 2.2 после размыкания ключа. Постройте примерные графики.
В задачах 2.2.1–2.2.25 найдите законы изменения напряжения uC(t) на емкости и тока iС(t) через емкость после коммутации. Постройте примерные графики.
Таблица 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.1 | 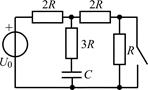 | 2.2.2 | 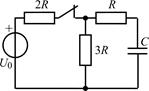 |
| 2.2.3 |  | 2.2.4 | 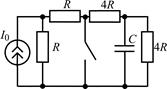 |
| 2.2.5 | 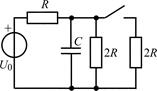 | 2.2.6 | 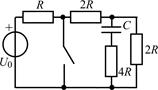 |
| 2.2.7 |  | 2.2.8 | 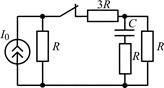 |
| 2.2.9 | 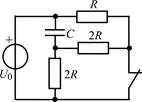 | 2.2.10 | 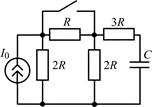 |
| 2.2.11 |  | 2.2.12 | 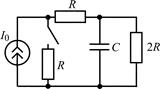 |
Продолжение табл. 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.13 | 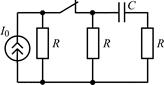 | 2.2.14 |  |
| 2.2.15 | 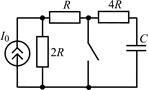 | 2.2.16 | 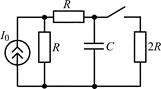 |
| 2.2.17 | 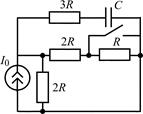 | 2.2.18 | 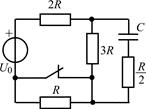 |
| 2.2.19 | 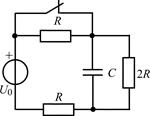 | 2.2.20 | 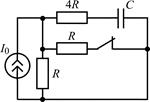 |
| 2.2.21 | 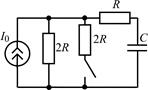 | 2.2.22 | 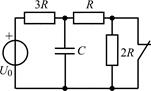 |
Окончание табл. 2.2
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.2.23 | 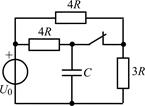 | 2.2.24 | 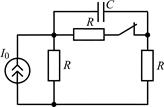 |
| 2.2.25 | 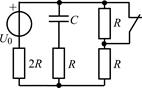 |
2.3. Анализ переходных колебаний в RL-цепях
при ненулевых начальных условиях
[1, с. 218–243; 2, с. 185–196]
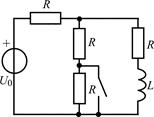 |
| Рис. 2.3 |
2.3.0. Найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности в цепи на рис. 2.3 после замыкания ключа. Постройте примерные графики.
В задачах 2.3.1–2.3.25 найдите законы изменения тока iL(t) в индуктивности и напряжения uL(t) на индуктивности после коммутации. Постройте примерные графики.
Таблица 2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.1 | 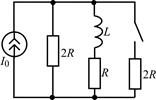 | 2.3.2 | 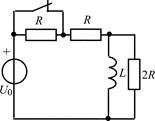 |
| 2.3.3 | 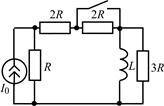 | 2.3.4 | 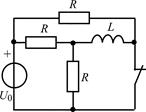 |
| 2.3.5 | 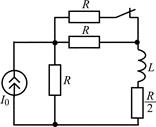 | 2.3.6 | 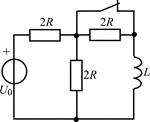 |
| 2.3.7 | 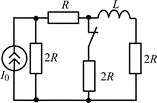 | 2.3.8 | 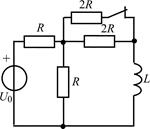 |
Продолжение табл.2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.9 | 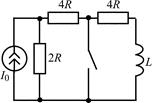 | 2.3.10 | 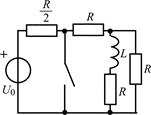 |
| 2.3.11 | 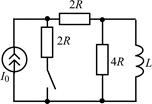 | 2.3.12 |  |
| 2.3.13 | 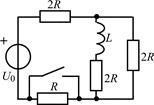 | 2.3.14 | 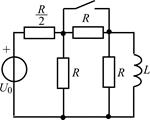 |
| 2.3.15 | 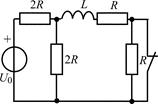 | 2.3.16 |  |
Окончание табл. 2.3
| Вариант | Схема цепи | Вариант | Схема цепи |
| 2.3.17 | 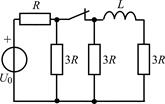 | 2.3.18 | 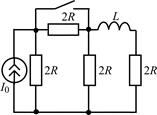 |
| 2.3.19 | 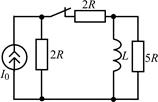 | 2.3.20 | 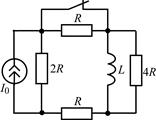 |
| 2.3.21 | 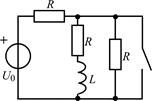 | 2.3.22 | 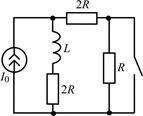 |
| 2.3.23 | 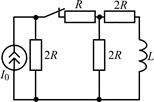 | 2.3.24 | 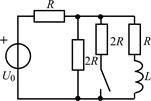 |
| 2.3.25 | 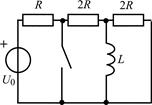 |
Контрольные вопросы
1. Какие функции преобразуемы по Лапласу?
2. Как связаны оригинал и изображение по Лапласу?
3. Сформулируйте основные свойства преобразования Лапласа.
4. Чему равны операторные сопротивления индуктивности, емкости, резистивного сопротивления?
5. Какие законы электрической цепи справедливы для L-изображений колебаний?
6. Как учитывается начальный запас энергии в индуктивности и емкости при составлении операторной схемы замещения цепи?
7. Нарисуйте операторные схемы замещения индуктивности и емкости при ненулевых начальных условиях.
8. Каков порядок анализа переходных колебаний в цепи операторным методом?
9. Сформулируйте теорему разложения.
10. Каков порядок нахождения оригинала по его L-изображению с помощью теоремы разложения?
11. Как по виду L-изображения реакции цепи найти ее постоянную времени t?
Видео:2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

Классический метод анализа переходных процессов
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Свободные и вынужденные составляющие токов и напряжений.
Классический метод анализа переходных процессов в линейных инвариантных во времени цепях с сосредоточенными параметрами основан на классическом методе решения обыкновенных дифференциальных уравнений. Как известно, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами (см. (1.46))
может быть представлено в виде суммы какого-либо частного решения этого уравнения и общего решения однородного дифференциального уравнения
которое получается из выражения (1.46) при f(t) = 0.
Общее решение однородного дифференциального уравнения (6.5) характеризует так называемые свободные процессы в цепи, т.е. процессы в цепи после коммутации в отсутствие внешних источников энергии (напомним (см. п. 1.5), что функция f(t) обращается в нуль при выключении всех независимых источников тока и напряжения).
Таким образом, характер свободных процессов не зависит от вида внешнего воздействия на цепь, а определяется только параметрами пассивных элементов и линейно управляемых источников, а также топологией цепи после коммутации.
Свободные процессы в цени протекают за счет разности энергий, соответствующих установившимся режимам работы цепи до и после коммутации. В связи с тем, что эта разность имеет конечное значение, свободные процессы в цепях с потерями с течением времени затухают (в идеализированных цепях без потерь свободные процессы имеют незатухающий характер).
Частное решение уравнения (1.46) определяет вынужденный режим работы цепи, т.е. режим, задаваемый действующими в цепи независимыми источниками энергии. Так как при анализе переходных процессов внешнее воздействие на цепь после коммутации изменяется по периодическому закону или сохраняет неизменное значение, в качестве частного решения (1.46) обычно выбирается установившееся значение реакции цени s после коммутации, т.е. значение реакции цени при
Очевидно, что вынужденная составляющая не зависит от режима работы цепи до коммутации и, следовательно, от начальных значений токов и напряжений.
Таким образом, при использовании классического метода анализа переходных процессов искомая реакция цепи s (ток или напряжение какой-либо ветви после коммутации) представляется в виде суммы свободной scn и вынужденной (принужденной) sBMH составляющих:
Для определения вынужденной составляющей реакции цепи можно воспользоваться рассмотренными ранее методами анализа линейных цепей в установившемся режиме. Если после коммутации токи независимых источников тока и напряжения независимых источников напряжения не изменяются, то с течением времени в цепи после коммутации установится режим постоянного тока. Очевидно, что в этом случае вынужденная составляющая реакции цепи будет являться постоянным током или напряжением.
Если после коммутации цепь находится под гармоническим воздействием определенной частоты, то вынужденная составляющая реакции цени также будет гармонической функцией времени и для расчета sBbIH можно воспользоваться методом комплексных амплитуд.
Если цепь после коммутации находится под воздействием нескольких независимых источников гармонических колебаний различной частоты, то, используя принцип наложения, мгновенное значение 5ВЫН можно определить как сумму мгновенных значений частичных токов или напряжений, вызванных в установившемся после коммутации режиме каждым из независимых источников в отдельности. Применяя принцип наложения, можно найти вынужденную составляющую реакции цени и в том случае, когда внешнее воздействие на цепь x(t) описывается периодической функцией более сложного вида, удовлетворяющей условиям Дирихле?, т.е. имеющей на конечном интервале конечное число максимумов и минимумов и конечное число разрывов первого рода. При этом функция x(t) может быть разложена в ряд Фурье (представлена в виде суммы гармонических колебаний кратных частот), а мгновенное значение 5ВЫН может быть получено как сумма мгновенных значений частичных токов или напряжений, вызванных в установившемся после коммутации режиме каждой из гармонических составляющих внешнего воздействия в отдельности.
Для определения свободной составляющей sCB реакции цепи необходимо найти v корней/?/ характеристического уравнения
соответствующего однородному уравнению (6.5). Если все корни уравнения (6.6) простые (различные), свободная составляющая реакции имеет вид
т.е. каждому простому корню р„ соответствует слагаемое свободной составляющей вида 
Если какой-либо корень р/, характеристического уравнения (6.6) имеет кратность п, то этому корню соответствует слагаемое свободной составляющей вида
Характеристическое уравнение (6.6) может иметь вещественные или комплексно-сопряженные корни, причем все корниpj характеристического уравнения линейной цепи, составленной из идеализированных пассивных элементов и независимых источников энергии, расположены в левой полуплоскости комплексного переменного р (включая и мнимую ось): Re|/>, ] 0). Дифференциальное уравнение цепи получают из системы уравнений электрического равновесия цепи при t • °°).
Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи (общее решение однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).
Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения цепи) находят путем суммирования свободной и вынужденных составляющих реакции цепи.
Определение постоянных интегрирования. Постоянные интегрирования находят, используя зависимые начальные условия (значения искомых токов или напряжений и их v — 1 первых производных в начальный момент времени после коммутации). Для определения зависимых начальных условий используют независимые начальные условия и уравнения электрического равновесия цепи при t = 0+.
Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя постоянные интегрирования в общее решение дифференциального уравнения цени после коммутации, находят частное решение дифференциального уравнения, соответствующее заданным начальным условиям, т.е. искомый ток или напряжение одной из ветвей при t > 0.
Переходные процессы в последовательной /?С-цени при скачкообразном изменении ЭДС. Рассмотрим переходные процессы в последовательной ДС-цеии (рис. 6.4, а) при скачкообразном изменении ЭДС идеализированного источника постоянного напряжения:
Такое изменение ЭДС источника напряжения происходит, например, когда в цепи, схема которой приведена на рис. 6.4, б, ключ S в момент времени t = 0 перебрасывают из положения 1 в положение 2. Очевидно, что в момент времени, непосредственно предшествовавший коммутации, напряжение на емкости равнялось напряжению на зажимах источника энергии при t 0
Дифференциальное уравнение рассматриваемой цепи можно составить относительно любой из неизвестных величин (напряжения на сопротивлении uRy напряжения на емкости Uq тока сопротивления iR, тока емкости ic), однако, учитывая, что для данной цепи известно начальное значение напряжения на емкости, целесообразно составить уравнение относительно этого напряжения.
Исключая из основной системы уравнений электрического равновесия цепи при t > 0
все неизвестные величины, кроме ис, получаем
Напряжение па емкости при t > О представим в виде суммы вынужденной иСиып и свободной иСса составляющих
Очевидно, что с течением времени после коммутации в цепи должен установиться режим постоянного тока, причем установившееся значение тока емкости равно нулю (сопротивление емкости постоянному току бесконечно велико), а установившееся значение напряжения емкости — напряжению источника энергии после коммутации. Таким образом, вынужденная составляющая напряжения па емкости
Характеристическое уравнение цепи RCp +1=0 имеет единственный корень
где тс = RC — постоянная времени последовательной /?С-цепи, поэтому свободная составляющая напряжения на емкости ис содержит один экспоненциальный член:
Используя выражения (6.10)—(6.12), находим напряжение емкости после коммутации при произвольных начальных условиях:
Для определения постоянной интегрирования Л! воспользуемся независимым начальным условием (6.9). Полагая в выражении (6.13) t = 0+, ис= ис(0+) = Е<, получаем Е = = Е2 + Ah откуда Ах = Е — Е2.
Таким образом, при заданных начальных условиях напряжение на емкости после коммутации (t > 0) описывается выражением
Зависимость напряжения на емкости от времени при различных соотношениях между Е и Е2 показана на рис. 6.4, в — Э, здесь же дана зависимость от времени тока емкости ic, которая при t > 0 определяется путем дифференцирования выражения (6.14) по времени и умножения результата на С
Как очевидно из рис. 6.4, в — д, в начальный момент после коммутации напряжение на емкости сохраняет то же значение, что и до коммутации, а затем плавно изменяется, стремясь в пределе к Е2. Ток емкости в начальный момент скачком изменяется от нуля до начального значения:
а затем плавно уменьшается, стремясь к нулю. В связи с гем, что установившееся значение тока емкости до и после коммутации равно нулю, ток рассматриваемой цепи содержит только свободную составляющую.
Анализ выражения (6.16) показывает, что начальное значение тока емкости /с(0+) численно равно постоянному току, который протекал бы в цепи после коммутации, если бы емкость С была заменена идеальным источником напряжения Е.
Следовательно, в начальный момент времени после коммутации емкость ведет себя подобно источнику напряжения, ЭДС которого равна начальному значению напряжения на емкости. Если начальное значение напряжения на емкости равно нулю, то в начальный момент после коммутации ветвь с емкостью можно считать короткозамкнутой, т.е. сопротивление емкости при t = 0+ равно нулю.
Далее (см. пример 6.4) будет показано, что в начальный момент времени после коммутации индуктивность ведет себя подобно источнику тока, ток которого равен начальному значению тока через индуктивность. При /ДО ) = 0 ветвь с индуктивностью в начальный момент времени можно считать разомкнутой, т.е. сопротивление индуктивности при t = 0+ имеет бесконечно большое значение.
Как следует из выражений (6.12) и (6.15), скорость затухания свободных составляющих тока и напряжения емкости не зависит от значений ЭДС идеализированного источника напряжения до и после коммутации, а определяется только постоянной времени цепи тс, которая численно равна промежутку времени, в течение которого свободные составляющие тока и напряжения уменьшаются в е
2,718 раз. Можно показать, что при любом t > 0
Таким образом, постоянная времени рассматриваемой цени численно равна длине подкасательной к кривой Uqb или iCcB при любом значении t > 0, т.е. длине отрезка временной оси, заключенного между какой-либо точкой t = t> О и точкой пересечения временной оси и касательной, проведенной к кривой иСса или iCcB в точке uCcB(t) или zCcB(?i). Для определения постоянной времени цепи касательную к кривым icCB или наиболее удобно проводить при t = 0. В этом случае она пересекает ось времени в точке t = тс (см. рис. 6.4, в — д).
Чем больше постоянная времени цепи, тем медленнее затухают свободные составляющие токов и напряжений, а следовательно у токи и напряжения цепи медленнее приближаются к установившимся значениям.
Теоретически процесс установления нового режима в цепи длится бесконечно долго. Однако, учитывая, что к моменту времени, равному Зт^ после коммутации, свободные составляющие уменьшаются до уровня менее 0,05 от начального значения, а к моменту времени, равному 5тс, — до уровня менее 0,01 от начального значения, переходные процессы в цепи можно считать практически закончившимися через промежуток времени 3-^5тс после коммутации.
Подключение к последовательной jRL-цепи источника гармонического напряжения. Рассмотрим переходные процессы в последовательной RL-цепи, содержащей идеализированный источник, ЭДС которого изменяется во времени по закону
Временная диаграмма e(t) при со > 0 приведена на рис. 6.5, а.
В этом случае ток индуктивности в момент времени, непосредственно предшествующий коммутации, iL(0_) = 0.
Дифференциальное уравнение цепи, составленное относительно тока i = ii, при t> 0 имеет вид
Вынужденная составляющая тока может быть найдена с помощью метода комплексных амплитуд:
Рис. 6.5. К исследованию переходных процессов при включении источника гармонического напряжения в последовательную RL-цсиь
где 
комплексного входного сопротивления цепи. Характеристическое уравнение цепи
имеет единственный корень р = -R/L, поэтому свободная составляющая тока содержит один экспоненциальный член:
где тi = L/R — постоянная времени последовательной /?1-цепи.
Суммируя свободную и вынужденную составляющие, находим общее решение дифференциального уравнения цепи (6.18) после коммутации:
Для определения постоянной интегрирования Л воспользуемся первым законом коммутации, в соответствии с которым начальное значение тока рассматриваемой цепи должно равняться нулю:
Подставляя равенство (6.20) в выражение (6.19), получаем
С учетом формулы (6.21) выражение для тока цепи после коммутации принимает вид
Характер переходных процессов в цепи зависит от соотношения между начальной фазой ф ЭДС идеализированного источника напряжения и аргументом ф входного сопротивления цепи. Если значения j/ и ф выбраны таким образом, что начальные значения вынужденной iBын(0+) и свободной *св(0+) составляющих равны нулю (ф = ф ± тс/2), то свободная составляющая тока тождественно равна нулю. Переходные процессы в цени в этом случае отсутствуют, т.е. установившийся режим наступает сразу же после коммутации. При |/ = ф или |/ = ф ± л начальные значения свободной и принужденной составляющих максимальны и различия в форме кривых i = i(t) и гпр = inp(t) выражены наиболее заметно (рис. 6.5, б).
Как и для последовательной /?С-цепи, скорость затухания свободной составляющей тока последовательной RL-цепи не зависит от характера внешнего воздействия, а определяется только постоянной времени xL. За промежуток времени t = t l свободная составляющая тока уменьшается в е раз и к моменту времени t = после коммутации переходные процессы в цепи можно считать практически закончившимися.
Подключение к последовательной RLC-цепи источника постоянного напряжения [1] . Последовательная RLC-цепьсодержит два независимо включенных реактивных элемента, поэтому процессы в ней описываются дифференциальным уравнением второго порядка, а для определения постоянных интегрирования необходимо задать два независимых начальных условия. Если ЭДС идеального источника напряжения изменяется во времени по закону
то независимые начальные условия цепи имеют нулевые значения
Составим уравнение электрического равновесия цепи по методу токов ветвей для t > О
Дифференцируя правую и левую части уравнения (6.23), получаем дифференциальное уравнение рассматриваемой цепи после коммутации:
Для определения единственного решения этого уравнения, соответствующего заданному режиму работы цепи до коммутации, необходимо найти начальные значения тока цепи и его первой производной по времени. Начальное значение тока цепи совпадает с начальным значением тока индуктивности:
а начальное значение первой производной тока цепи по времени может быть найдено с использованием независимых начальных условий (6.22) и уравнения электрического равновесия цени (6.23) при t = 0+:
В связи с тем, что установившееся значение тока этой цени после коммутации равно нулю, ток при t > 0 содержит только свободную составляющую: i = iCB.
Характеристическое уравнение последовательной RLC- цепи
имеет два корня:
где 5 = R/(2L) — коэффициент затухания; со0 = 1/VZ.C — резонансная частота цепи. В зависимости от соотношения между величинами со0 и 8 или, что то же самое, в зависимости от добротности цепи
корни характеристического уравнения (6.27) могут быть вещественными различными, комплексно-сопряженными или вещественными одинаковыми (кратными). Рассмотрим каждый из этих случаев.
Вещественные различные корни. При малой добротности последовательной RLC-цепи (Q 2р и 8 > со0) характеристическое уравнение (6.27) имеет два различных вещественных отрицательных корня, а выражение для тока цепи после коммутации (t > 0) содержит два экспоненциальных члена:
Дифференцируя правую и левую части выражения (6.29) di/dt = РАхе р $ + р2А2е р ^ и используя зависимые начальные условия (6.25), (6.26), составляем уравнения для определения постоянных интегрирования А и А2:
откуда
С учетом уравнений (6.30) выражение для тока цепи после коммутации принимает вид
Расположение корнейР,Р2 характеристического уравнения в плоскости комплексного переменного р и зависимость нормированного тока исследуемой цепи от времени приведены на рис. 6.6, а. Переходный процесс в цепи носит апериодический (неколебательный) характер, причем вследствие того, что |р(| (2) затухает быстрее, чем первая г (1) .
Комплексно-сопряженные корни. При большой добротности последовательной RLC-цепи (Q> 1/2, т.е. R 2 — частота свободных колебаний в цепи (смысл этого понятия будет ясен из последующего изложения). Ток цепи после коммутации, как и в предыдущем случае, определяется выражением (6.29), которое после нахождения постоянных интегрирования А = E/(J2(oCBL), А2 = = -?У(/2сосв1) может быть с учетом соотношения
преобразовано к виду
где
Таким образом, при включении в последовательную RLC-цепъ с высокой добротностью идеального источника постоянного напряжения переходные процессы в ней имеют колебательный характер. Ток цепи представляет собой затухающую гармоническую функцию (точнее, квазигармо- ническую функцию), амплитуда которой /,„(/) экспоненциально уменьшается во времени. Колебательный характер переходного процесса в цепи связан с периодическим обменом энергией между емкостью и индуктивностью, а затухание колебаний объясняется потерями энергии в сопротивлении. Расположение корней ри р2 характеристического уравнения в плоскости комплексного переменногор и зависимость тока цепи от времени показаны на рис. 6.6, б. Корни характеристического уравнения расположены симметрично относительно действительной оси в левой полуплоскости на полуокружности радиусом, численно равным резонансной частоте последовательного колебательного контура оо0— Чем меньше коэффициент затухания 8, тем ближе к мнимой оси расположены корни уравнения, меньше различие между сосв и ш0 и медленнее затухание свободных процессов. В пределе, при 8 = 0, корни характеристического уравнения располагаются на мнимой оси, частота свободных колебаний совпадает с резонансной частотой цепи, а колебательные процессы в цепи носят незатухающий характер (рис. 6.6, в). Таким образом, резонансная частота RLC-цепи численно равна частоте свободных колебаний для случая, когда коэффициент затухания 8 = 0.
Штриховыми линиями на рис. 6.6, б показаны кривые которые характеризуют закон изменения амплитуды тока во времени. Эти кривые называются огибающими. Величина, численно равная длине подкасательной к огибающей тока
называется постоянной времени последовательной RLC-цепи.
Очевидно, что за промежуток времени t = т ордината огибающей тока уменьшается в е раз. Из сравнения выражений (6.31) и (3.69) следует, что постоянная времени последовательной RLC-цепи обратно пропорциональна половине полосы пропускания одиночного колебательного контура на уровне 1/У2:
Таким образом, чем уже полоса пропускания контура, тем медленнее затухают в нем свободные составляющие токов и напряжений
Скорость затухания свободных процессов в рассматриваемой цепи может быть охарактеризована также логарифмическим декрементом колебаний 0, который равен натуральному логарифму отношения двух максимальных значений тока, взят ых через период свободных колебаний Тсв = 2я/сосв =
Найдя натуральный логарифм отношения ординат огибающих тока для t > 0 и t + Гсв, можно прийти к выводу, что логарифмический декремент колебаний не зависит от выбора t, а определяется только добротностью цепи Q
Анализ данного выражения показывает, что логарифмический декремент колебаний равен нулю при 8 = О (Q = °°) и обращается в бесконечность при 5 = со0 (Q = 1/2).
Определим отношение Зт (промежуток времени, за который свободные составляющие уменьшаются до уровня 5% от начального значения) к периоду свободных колебаний Гсв:
Следовательно, добротность одиночного колебательного контура приближенно равна числу периодов свободных колебапий, укладывающихся па интервале затухания свободных составляющих до уровня 5% от начального.
Кратные корни. При Q = 1/2, т.е. при R = 2р и 5 = оо0> ха_ рактеристическое уравнение последовательной /XX-цен и имеет два одинаковых вещественных корня Р=Р2 = -б, расположенных на отрицательной вещественной полуоси в плоскости комплексного переменного р (рис. 6.6, г). Как следует из выражения (6.8), общее решение дифференциального уравнения (6.24) при t > 0 в этом случае имеет вид
Определяя с помощью зависимых начальных условий (6.25) и (6.26) значения постоянных интегрирования А = О, Л2 = E/L и подставляя их в выражение (6.32), окончательно получаем
Как и в случае вещественных различных корней, переходный процесс в цепи при одинаковых вещественных корнях имеет апериодический характер (см. рис. 6.6, г), поэтому условие Q=l/2 является предельным условием существования в цепи апериодических свободных процессов. Режим работы цепи на границе между колебательным и апериодическим переходными процессами называется критическим.
Таким образом, характер переходных процессов в последовательной RLC-цепи полностью определяется расположением корней характеристического уравнения в плоскости комплексного переменного.
Описанная зависимость характера переходных процессов в цепи второго порядка от расположения корней характеристического уравнения в плоскости комплексного переменного присуща не только последовательной /XX-цени, она является общим свойством линейных электрических цепей любого порядка сложности.
Подключение к последовательной ЛТС-цепи источника гармонического напряжения. Рассмотрим важный для практики случай включения источника гармонического напряжения в последовательную /XX-цепь с высокой добротностью (Q X 1/2). Свободные процессы в такой цепи, как было установлено выше, имеют колебательный характер. Пусть идеализированный источник напряжения включен в цепь в момент времени t = 0 (см. выражение (6.17)), причем примем, что мгновенное значение ЭДС этого источника при t = 0 равно нулю (р = -л/2). Уравнение баланса напряжений такой цепи после коммутации имеет вид
а дифференциальное уравнение цепи
Для решения уравнения (6.34) необходимо определить начальные значениятока цепи г(0+) и его первой производной по времени
Используя независимые начальные условия 
Суммируя вынужденную и свободную составляющие тока
находим общее решение уравнения (6.34) при t > 0:
где 
составляющей тока; 
Для определения постоянных интегрирования Ait А2 продифференцируем правую и левую части выражения (6.38):
и подставим в выражения (6.38) и (6.39) зависимые начальные условия (6.35). Решая полученную таким образом систему уравнений относительно Л), и А2, получаем
С учетом соотношений (6.40) выражение (6.37) для свободной составляющей тока может быть преобразовано к виду
Предположим, что частота внешнего воздействия ш близка к частоте свободных колебаний сосв, а добротность Q настолько велика, что сосв практически совпадает с резонансной частотой цепи со0.
С учетом этих допущений, которые незначительно уменьшают общность получаемых результатов, выражение (6.41) существенно упрощается:
Таким образом, в последовательной RLC-цепи, удовлетворяющей принятым допущениям, свободная составляющая тока является затухающей гармонической функцией времени. В начальный момент времени амплитуда свободной составляющей тока равна амплитуде вынужденной составляющей, а затем уменьшается по экспоненциальному закону. Через промежуток времени, равный 3-^5т после коммутации, амплитуда свободной составляющей становится пренебрежительно малой по сравнению с амплитудой вынужденной составляющей, и переходный процесс в цепи можно считать практически закончившимся.
Ток цепи после коммутации равен сумме свободной и вынужденной составляющих:
Если частота внешнего воздействия совпадает с резонансной частотой цепи coq, то входное сопротивление цепи име-
Рис. 6.7. Зависимость тока последовательной RLC-цепи от времени при включении источника гармонического напряжения:
ет чисто резистивный характер (ф = 0) и выражение (6.42) принимает вид (рис. 6.7, а)
Как очевидно из рисунка, амплитуда тока цепи при со = coq плавно увеличивается во времени, стремясь в пределе к установившемуся значению 1т вьш. Ни при каких значениях t амплитуда тока после коммутации не превышает этого значения.
При включении в последовательную RLC-цепь источника гармонического напряжения, частота которого близка к резонансной, но не равна ей, в цепи наблюдаются биения, заключающиеся в периодическом увеличении амплитуды тока или напряжения до значения, значительно превышающего амплитуду вынужденной составляющей (рис. 6.7, б). Если пренебречь затуханием свободной составляющей тока (8 = 0), то из выражения (6.42) получаем
Как следует из выражения (6.44), в рассматриваемом случае ток цепи имеет частоту, близкую к резонансной ((со + coq)/2
со0), амплитуда тока медленно изменяется во времени:
а максимальное значение тока в переходном режиме в два раза превышает амплитуду вынужденной составляющей.
Возникновение биений при включении источника гармонического напряжения в последовательную RLC-цепь объясняется тем, что вследствие несовпадения частот внешнего воздействия и свободных колебаний фазовые соотношения между свободной и вынужденной составляющими тока непрерывно изменяются, причем разность мгновенных фаз этих колебаний (со — со0)Г линейно нарастает во времени. В те моменты времени, когда разность мгновенных фаз равна 2kn, где k = О, 1,2, сумма мгновенных значений /св и гвын минимальна, а в те моменты времени, когда разность фаз равна (2k + 1 )тг, — максимальна. Частотой биений называют частоту повторения максимумов огибающей тока (6.45). Угловая частота биений, таким образом, равна абсолютному значению разности угловых частот свободной и вынужденной составляющих:
В реальных колебательных контурах коэффициент затухания имеет малое, но конечное значение. Свободная составляющая тока в таких контурах экспоненциально уменьшается во времени, а биения носят затухающий характер.
Видео:Переходные процессы. Анализ разветвленной цепи 2 порядка. Часть 1Скачать

Анализ переходных колебаний в разветвленных rc цепях путем составления дифференциального уравнения
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи
| Резистор (идеальное активное сопротивление) | |||||||
| Катушка индуктивности (идеальная индуктивность) | |||||||
| Конденсатор (идеальная емкость) | |||||||
| . | (1) |
Подставив в (1) значение тока через конденсатор
,
получим линейное дифференциальное уравнение второго порядка относительно
.
В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
| , | (2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); — известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); — к-й постоянный коэффициент, определяемый параметрами цепи.
Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
| , | (3) |
где и — соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; — число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); — число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).
Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).
Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.
Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная — свободной составляющей.
В соответствии с вышесказанным, общее решение уравнения (2) имеет вид
| (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).
Таблица 2. Законы коммутации
Первый закон коммутации (закон сохранения потокосцепления)
Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .
Второй закон коммутации (закон сохранения заряда)
Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и , что приводит к нарушению законов Кирхгофа.
На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .
второй закон коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:
Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .
Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.
В соответствии с законами коммутации
и .
На основании второго закона Кирхгофа для момента коммутации имеет место
,
и .
Для известных значений и из уравнения
определяется .
Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)
.
Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).
Таблица 3. Выражения свободных составляющих общего решения
Вид корней характеристического уравнения
Выражение свободной составляющей
Корни вещественные и различные
Корни вещественные и
Пары комплексно-сопряженных корней
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением
,
которое называется декрементом колебания, или натуральным логарифмом этого отношения
,
называемым логарифмическим декрементом колебания, где .
Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:
,
где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
📹 Видео
Переходный процесс в RC-цепи — вывод формул. Часть 1 (видео 24) | Анализ цепей | ЭлетротехникаСкачать

Переходный процесс в RC-цепи — объяснение (видео 26)| Анализ цепей | ЭлетротехникаСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

69997 Анализ переходных процессов в RC-цепях – 1Скачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Основы электротехники. 06. Переходные процессыСкачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Пример 7 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

Пример 5 | Классический метод расчета цепи первого порядка с катушкойСкачать

Расчет переходного процесса RLC цепи Классическим методомСкачать

Лекция 122. Переходные процессыСкачать

ТОЭ 78. Переходные процессы в электрических цепях, составление характеристических уравнений 1 способСкачать

Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Составление дифференциального уравненияСкачать




































































