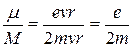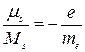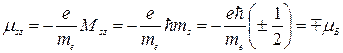- Орбитальный момент Angular Momentum
- Орбитальный механический момент частицы и уравнения на его собственные значения
- 12.1. Оператор орбитального момента
- 12.2. Проекция углового момента
- 12.3. Собственные функции оператора проекции момента
- 12.4. Соотношение неопределённостей для проекции момента
- 12.5. Оператор квадрата углового момента
- Собственные значения квадрата момента
- 12.6. Собственные функции оператора квадрата момента
- 12.7 Чётность состояния
- АТОМЫ В МАГНИТНОМ ПОЛЕ
- 📸 Видео
Орбитальный момент
Angular Momentum
Орбитальный момент — момент количества движения частицы, обусловленный её движением в пространстве.
Величина орбитального момента количества движения L дается соотношением
l — орбитальное квантовое число.
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной число l, имея в виду, что между l и L имеется однозначная связь L 2 = ћ 2 l(l + 1).
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения квантуется. Например, для частицы с l = 2 момент количества движения
Для сравнения укажем, что орбитальный момент количества движения Земли вокруг Солнца больше в
10 74 раз.
Для характеристики состояний с различными значениями орбитального числа l обычно используют спектроскопические названия орбитальных моментов в соответствии со следующей таблицей.
Таблица. Спектроскопические названия орбитальных чисел l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и т. д. | |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций.
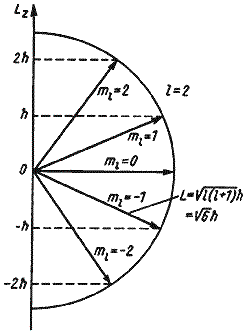
Рис. Возможные ориентации вектора 
Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 
т. е. от направления вектора 
Видео:99. Квантование момента импульсаСкачать

Орбитальный механический момент частицы и уравнения на его собственные значения
Теория углового момента является неотъемлемой частью учения об атоме. Классификация атомных уровней энергии во многом выполняется с помощью квантовых чисел углового момента. Момент вращения имеет размерность действия, поэтому его принято выражать в единицах постоянной Планка ħ. Полный момент ħj любой частицы в квантовой теории состоит из орбитального момента вращения ħl и внутреннего момента, или спина ħs. Значения l и s квантуются. Орбитальный момент может принимать только неотрицательные целые значения ħ:
а спин — целые и полуцелые:
(2) s = 0, 1/2, 1, 3/2, 2, 5/2,
В этой главе мы изложим сведения об орбитальном моменте.
Видео:Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать

12.1. Оператор орбитального момента
В классической механике момент количества движения, или угловой момент, определяется как векторное произведение радиус-вектора частицы на её импульс:
В квантовой механике классические соотношения справедливы для операторов и для средних значений. Напомним формулы (8.4.3) и (8.4.6) для операторов координаты и импульса:
Из трёх приведённых формул следует выражение для оператора орбитального момента:
Здесь ex , ey и ez — единичные векторы, направленные вдоль осей x , y и z , соответственно. С помощью (1.3) можно выписать операторы проекций момента на оси прямоугольной системы координат. Например,
Аналогичные формулы справедливы и для других проекций момента вращения.
Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

12.2. Проекция углового момента
В теории атома ключевую роль играет приближение центрально–симметричного поля. Известно, что в случае центральной симметрии сохраняются энергия и вектор момента частицы. В связи с этим полезно перейти к сферической системе координат, в которой положение частицы в пространстве задаётся расстоянием r от начала координат и двумя углами: полярным θ и азимутальным φ . Пользуясь рис.12.2.1, найдём связь между
сферическими и декартовыми координатами:
Покажем, что оператор lz в сферической системе координат пропорционален производной ∂ /∂φ. Для этого вычислим её в декартовой системе:
Из (2.1) следует, что третье слагаемое справа равно нулю вместе с ∂z /∂φ. Продифференцируем по φ первые две формулы (2.1). формулы для x и y :
Теперь ясно, что


Определим собственные функции и собственные значения нового оператора.
Видео:Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

12.3. Собственные функции оператора проекции момента
Задача на собственные значения оператора проекции момента
согласно (2.2), приводит к дифференциальному уравнению
решением которого является функция
Набор допустимых значений lz в данном случае определяется требованием однозначности волновой функции:
(3.3) Φ(φ + 2π) = Φ(φ),
из которого вытекает условие
Напомним известный из теории комплексных чисел факт, что уравнение
имеет бесконечное множество решений:
Но если фиксирован модуль вектора момента, то его проекция на одну из осей не может принимать сколько угодно большие значения. Следовательно, величина | m| ограничена сверху. Обозначим посредством l её максимально возможное значение. Тогда из (3.4) следует правило квантования проекции углового момента:
Здесь m принимает только целые значения — положительные и отрицательные, включая нуль:
всего 2l + 1 разных проекций. Параметр l играет важную роль в теории атома, его называют орбитальным квантовым числом, иногда — просто «моментом». Правило квантования
проекции момента иллюстрирует рис.12.3.1 для l = 0, 1, 2, 3. Величина m полностью определяет собственные функции оператора l z , поэтому будем нумеровать их индексом « m ». Нормировочный множитель N вычисляем из условия


Итак, нормированная волновая функция, описывающая состояние с определённым значением lz, равна:

Параметр m играет важную роль в теории эффекта Зеемана. Поэтому его называют «магнитным» квантовым числом. Плотность вероятности
одинакова для всех значений φ. Это означает, что при наличии выделенного направления полная вероятность обнаружения частицы имеет аксиальную симметрию. Выделенное направление может задавать однородное магнитное или электрическое поле, направленное вдоль вертикальной оси.
В случае сферической симметрии направление оси z заранее ничем не выделено. Следовательно, стационарные состояния, отличающиеся только значением проекции lz, в отсутствие внешних полей имеют одинаковую энергию. Таким образом, энергетические уровни системы с отличным от нуля моментом l вырождены 2l + 1 раз.
Видео:Что такое спин?Скачать

12.4. Соотношение неопределённостей для проекции момента
Выше, в седьмой главе мы познакомились с двумя парами канонически сопряженных величин:
«энергия

Они связаны формулами (7.1.2) и (7.1.3). Оператор энергии пропорционален производной по времени, а оператор импульса — оператору градиента. Волновая функция стационарного состояния зависит от произведения Et, а состояния с известной проекцией импульса px — от произведения pxx:
(формулы для проекций импульса на оси « y » и « z » легко написать по аналогии со второй строкой). Напомним, что канонически сопряжённые величины подчиняются соотношению неопределённостей:
Теперь рассмотрим пару

Из (2.2) и (3.6) видно, что оператор проекции момента сопрягается с углом φ так же, как энергия со временем и координата с импульсом. Распространим эту аналогию и на соотношение неопределённостей:
Итак, если мы точно измерили величину l z , то угол φ остаётся полностью неопределённым, а вместе с ним — и проекции l x и l y . Это свойство квантового момента вращения в корне отличает его от классического, все три проекции которого могут быть измерены точно. Например, если проекция момента на вертикальную ось принимает максимально возможное значение, то это не означает, что сам вектор направлен вдоль этой оси. При m равном l вектор момента наклонён по отношению к оси « z ». В противном случае обе проекции — l x и l y — имели бы вполне определённые, равные нулю значения, в противоречии с (4.1). Таким образом, длина вектора |l| превышает величину l. Единственным исключением является момент, равный нулю. В этом случае все три его проекции одновременно равны нулю:
а вопрос о направлении вектора лишён смысла.
Изложенные свойства орбитального момента имеют наглядное геометрическое истолкование в так называемой векторной модели момента, согласно которой вектор момента вращения прецессирует вокруг вертикальной оси. Наглядно прецессия изображена на рис.12.4.1. Определённые
значения при этом имеют модуль вектора l и его проекция lz. Проекции lx и ly быстро осциллируют и в среднем равны нулю.
Видео:Консультация по квантовой механике. Часть 7. "Спин электрона"Скачать

12.5. Оператор квадрата углового момента
Возведём в квадрат выражение (1.2). Опуская несложные, но длинные математические выкладки, напишем окончательный результат:
где посредством ∆θ,φ обозначена угловая часть оператора Лапласа:
Собственные значения и собственные волновые функции оператора квадрата момента получаются путём решения дифференциального уравнения
при дополнительных требованиях конечности и однозначности волновой функции. Здесь l 2 обозначает собственное значение квадрата момента.
Собственные значения квадрата момента
В сферически-симметричном случае средние значения квадратов проекций равны друг другу:
а в сумме они дают среднее значение квадрата момента. Отсюда:
С другой стороны, в состоянии с определённым значением квадрата момента среднее значение совпадает с собственным значением:
Среднее значение квадрата проекции lz равно сумме квадратов всех проекций из набора (3.5), делённой на число слагаемых:
Подставляя это выражение в (5.4), приходим к окончательному результату:
Тот факт, что собственное значение квадрата момента превышает квадрат максимального значения проекции l , находится в согласии с изложенным выше соотношением неопределённостей для проекций момента на разные оси. Параметр l полностью определяет величину квадрата момента, поэтому для краткости его принято называть «моментом», или «абсолютным значением момента», имея в виду соотношение (5.5).
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

12.6. Собственные функции оператора квадрата момента
Математическая часть этой задачи достаточно сложна. Поэтому приведём без доказательства результат, известный из теории специальных функций. Уравнение (5.3) имеет однозначное и ограниченное решение только в том случае, если выполнено условие (5.5), причём параметр l может принимать любое значение из ряда (1).В этом случае его решением являются сферические функции Ylm(θ,φ), зависящие от орбитального l и магнитного m квантовых чисел. Таким образом, сферические функции удовлетворяют уравнению
Собственное значение квадрата момента l ( l +1) действительно превышает квадрат максимально возможного значения l проекции момента на выделенное направление. Этот результат полностью согласуется с изложенным выше принципом неопределённости для вектора момента.
Сферические функции могут быть представлены в виде произведения двух сомножителей, один из которых является функцией только угла θ, а другой — только угла φ:
причём Φm(φ) — волновая функция проекции момента (3.6).
Волновая функция квадрата момента полностью определяется двумя квантовыми числами — l и m . В рамках векторной модели рис.12.4.1 это может быть наглядно представлено как вращение вокруг оси « z » вектора, вадрат модуля которого равен
но максимальная проекция на ось не превышает l. Проекции момента на оси «x» и «y» при этом не определены, а их средние значения равны нулю.
Зависимость волновой функции от угла θ сводится к известным из математики присоединённым полиномам Лежандра. Для m ≥ 0:
Из теории специальных функций известна общая формула для присоединённых полиномов Лежандра:
Здесь так же, как и в (6.3) предполагается, что m ≥ 0. В случае отрицательных значений m следует выполнить замену
Нормированная волновая функция состояния с заданными квантовыми числами l и m равна
причём нормировка предполагает интегрирование по всему телесному углу. Выпишем несколько первых полиномов:
Им соответствуют волновые функции:
Состояния с нулевым значением момента (l = 0) принято называть s-состояниями, а квантовое число l равное единице, соответствует так называемым p–состояниям. Согласно (3.5), в s-состоянии возможно только одно значение магнитного квантового числа: m = 0, а p-состоянию отвечают три возможные проекции: m = 0, ±1.
Квадрат модуля функции Φ(φ), согласно (3.7), не зависит от угла φ. Поэтому вероятность W найти частицу в определённом объёме пространства пропорциональна | Pl m (cosθ) | 2 , то есть, полностью определяется полярным углом θ . На рис.12.6.1 приведена
полярная диаграмма для изотропного s‑состояния и анизотропных p‑состояний . Знак m для вероятности не имеет значения, так как она не зависит от угла φ . Можно считать, что положительный знак соответствует вращению горизонтальной гантели по часовой стрелке, а отрицательный — в противоположном направлении.
Видео:Что такое спин и почему он так важен для физики?Скачать

12.7 Чётность состояния
В квантовой теории излучения важную роль играет оператор инверсии Î. Он действует на координаты волновой функции, меняя их знаки на обратные:
Его собственные функции определяются уравнением
где I — собственное значение. Двукратное применение оператора инверсии приводит к тождеству:
Из (7.2) и (7.3) следует
Таким образом, собственные функции оператора инверсии либо не меняются вовсе при его воздействии, либо меняют свой знак. В первом случае говорят, что функция описывает чётное состояние, во втором — нечётное. Итак, чётная волновая функция удовлетворяет условию
а для нечётной функции справедливо
В квантовой теории имеет место закон сохранения чётности: если состояние замкнутой системы обладает определённой чётностью (чётное или нечётное), то она сохраняется со временем.
Определим чётность состояния частицы с заданным моментом l . Сначала преобразование инверсии
запишем в сферической системе координат. В–первых, ясно, что инверсия не меняет длины радиус–вектора:
Далее, из z → – z , согласно (2.1), вытекает
Функция cosθ меняет знак в двух случаях изменения аргумента: θ → π ± θ . Условию (2.1 a ) отвечает только один из них:
При этом сохраняется прежним знак sinθ . Следовательно, преобразование x → – x и y → – y , как указывают первые две строки (2.1), требует одновременной смены знака функций sinφ и cosφ :
что возможно в единственном случае:
Формулы (7.7 b , c ) выражают изменение углов θ и φ при операции инверсии. Их иллюстрирует
рис.12.7.1. На левом рисунке пунктиром обозначен экватор, а на правом ось « z » направлена на читателя.
Зависимость ψ( r ) от углов определяется собственной функцией орбитального момента (6.7), пропорциональной 
(7.8) 
Поясним последнюю формулу. Многочлен ( x 2 –1) l содержит только чётные степени x :
Каждая операция дифференцирования понижает его степень на единицу. Поэтому старшая степень (l+m)–й производной равна 2 l – l – m = l – m , и все слагаемые имеют одну и ту же чётность:
(7.9)
Множитель в круглых скобках является чётным, поэтому чётность (7.9) определяется множителем x l – m , что и доказывает (7.8).
Таким образом, полная волновая функция умножается на произведение (–1) l – m · (–1) m = (–1) l , и чётность состояния с данным значением l равна
Мы видим, что при чётном l волновая функция является чётной, а при нечётном — нечётной.
Видео:Квантовая механика 2 - Эксперимент Штерна-Герлаха. Спин электрона.Скачать

АТОМЫ В МАГНИТНОМ ПОЛЕ
1. Орбитальный механический и магнитный моменты электрона.
2. Спин электрона.
3. Опыт Штерна и Герлаха.
1.Орбитальный механический и магнитный моменты электрона.Пусть электрон движется со скоростью v по орбите радиуса r . Через площадку, расположенную в любом месте на пути электрона, за время t переносится заряд q = eνt, где e – заряд электрона, ν – число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы
I = 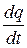

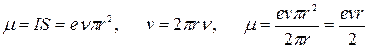
где v – скорость движения электрона.
Момент обусловлен движением электрона по орбите, вследствие чего его назвали орбитальным магнитным моментом электрона. Направление вектора μобразует с направлением тока правовинтовую систему, а с направлением движения электрона – левовинтовую.
Орбитальный механический момент импульса 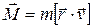
Отношение магнитного момента электрона к его механическому моменту называется гиромагнитным отношением. Получим
По Бору М = mvr = nћ. Следовательно,
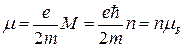
где 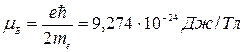
Из решения уравнения Шредингера для атома водорода мы получили, что квантование момента импульса по величине отличается от квантования его по Бору и определяется орбитальным квантовым числом l :
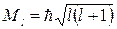
Квантуется также его проекция на некоторую заданную ось z, т.е. момент импульса электрона может иметь лишь такие ориентации в пространстве, для которых проекция 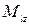
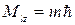
Таким образом, вектор собственного механического момента может принимать 2l +1 ориентацию в пространстве.
2.Спин электрона. В 1925 году Гаудсмит и Уленбек выдвинули гипотезу о том, что электрон обладает собственным механическим моментом импульса, не связанным с движением электрона в пространстве. Этот собственный момент был назван спином. Они дали спину наглядное модельное представление: спин – момент импульса, связанный с вращением электрона – заряженного шарика, вокруг своей оси. Однако скоро пришлось отказаться от подобных модельных представлений. Вращение электрона должно было бы происходить с такой угловой скоростью, что линейная скорость на поверхности его сферы в 200 раз превышала бы скорость света; либо размер электрона должен был превышать размеры атома; либо масса электрона превышала массу протона.
Спин и связанный с ним собственный (спиновый) магнитный момент следует считать внутренними свойствами, присущими электрону, подобно тому, как ему присущи заряд и масса. В отличие от орбитального момента спин всегда сохраняется. Спином обладают не только электроны, но и другие элементарные частицы – протоны, нейтроны, фотоны и др., кроме мезонов.
Величина собственного момента импульса электрона определяется по общим законам квантовой механики так называемым спиновым квантовым числомs
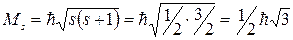
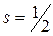
Проекция спина на заданное направление может принимать квантованные значения, отличающиеся друг от друга на ħ
С собственным механическим моментом связан собственный магнитный момент. Ряд опытных фактов свидетельствовал, что отношение собственных магнитного и механического моментов равно
Отсюда собственный магнитный момент электрона равен
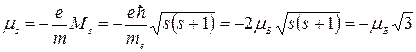
Знак минус указывает на то, что механический и магнитный моменты электрона направлены в противоположные стороны.
Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения
Таким образом, проекция собственного момента импульса электрона может принимать значения 
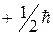
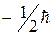
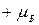
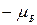
В ряд формул входят не сами моменты, а их проекции, поэтому принято говорить, что спин электрона равен одной второй (подразумевается в единицах ħ), а собственный магнитный момент равен одному магнетону Бора.
Магнитный момент атома складывается из орбитальных и собственных моментов входящих в его состав электронов, а также магнитного момента ядра (который обусловлен магнитными моментами входящих в состав ядра элементарных частиц). Магнитный момент ядра значительноменьше моментов электронов, поэтому при рассмотрении многих вопросов им можно пренебречь и считать, что момент атома равен векторной сумме магнитных моментов электронов.
3.Опыт Штерна и Герлаха.Посмотрим, каким образом можно было бы непосредственно убедиться в существовании спина и магнитного момента электрона. Очевидно, что для этого необходимо подвергнуть электрон действию внешнего магнитного поля. Наиболее подходящими для этой цели являются атомы водорода и элементов первой группы периодической системы. Невозбужденные состояния этих атомов принадлежат к типу s –состояний, т.е. орбитальный момент их равен нулю. Если опыт покажет, что эти атомы все-таки имеют механический и магнитный моменты, то их наличие можно приписать свойствам самого валентного электрона. Такой опыт был поставлен Штерном и Герлахом.
В закрытый сосуд помещали маленькую печку К, куда клали кусочек серебра. При нагревании серебро испарялось, и атомы его вылетали из отверстия печки во всевозможных направлениях с тепловыми скоростями порядка нескольких сот метров в секунду. С помощью нескольких щелей выделяли узкий пучок атомов серебра – атомный луч, который проходил через сильно неоднородное магнитное поле между полюсами электромагнита SN и попадал на пластину РР, где можно было обнаружить след осевших атомов. В неоднородном магнитном поле на атомы пучка должна действовать сила
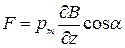
величина и знак которой зависят от угла α, образуемого вектором 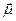
Таким образом, опыт Штерна и Герлаха показал, что углы, под которыми ориентируются магнитные моменты атомов по отношению к магнитному полю, могут иметь только дискретные значения, т.е. проекция магнитного момента на направление поля квантуется.
Опыт, впервые поставленный с серебром, был проделан затем с атомами других веществ. Опыт показал, что в случае водорода, серебра и щелочных металлов возникают две полоски, расположенные симметрично относительно полоски, которая получается в отсутствие поля. Это свидетельствует о том, что при прохождении через поле пучок разбивается на два пучка, одинаково отклоняющиеся в противоположные стороны. То есть проекция собственного момента импульса электрона может принимать только два значения, одинаковых по величине и противоположных по знаку. При отсутствии у электрона спина в s-состоянии расщепление пучка не наблюдалось бы, так как орбитальный магнитный момент атома в этом случае равен нулю. Таким образом в опыте было доказано существование спина. Расчет проекции магнитного момента атома на направление поля показал, что он равен численно одному магнетону Бора.
Опыт Штерна и Герлаха наряду с немногими другими принадлежит к числу основных опытов атомной физики, так как он обнаруживает одно из важнейших свойств материи.
Вопросы для самоконтроля
1.В чем заключается квантование момента импульса?
2.Что такое спин? Имеет ли он классический аналог?
📸 Видео
Квантовая механика и релятивистская теорияСкачать

Клёнов Н. В. - Атомная физика - Спин. Спин-орбитальное взаимодействие (Лекция 9)Скачать

Что такое СПИН? спин 1/2 и 3/2Скачать

СпинСкачать

Урок 460. "Портрет" атома водорода. Многоэлектронные атомыСкачать

Квантовая механика. Лекция 13 - СпинСкачать

Лекция №08 "Тождественность частиц и обменное взаимодействие"Скачать

Атомная и ядерная физика. Лекция 11.1. Спин-орбитальное взаимодействиеСкачать

Атомная физика. Лекция 11. Момент импульса частицы в квантовой механикеСкачать

Квантовая механика (иеханические и магнитные моменты)Скачать

Урок 459. Обзор квантовой теории атома водородаСкачать