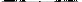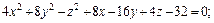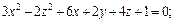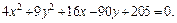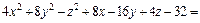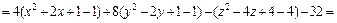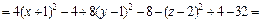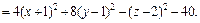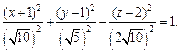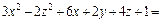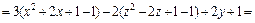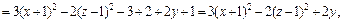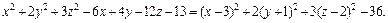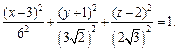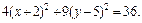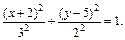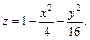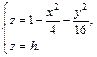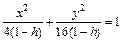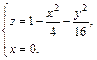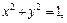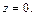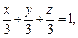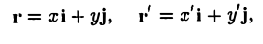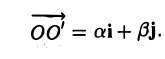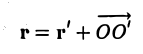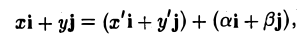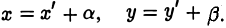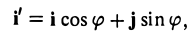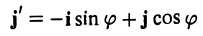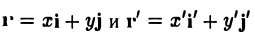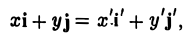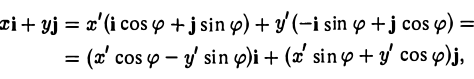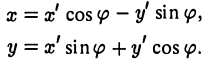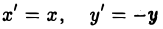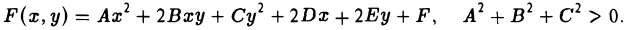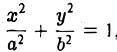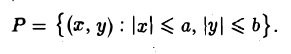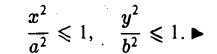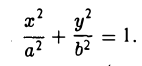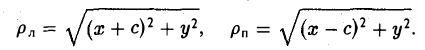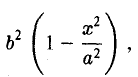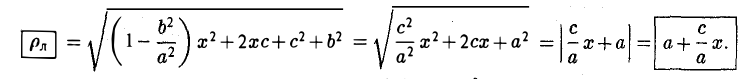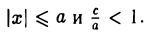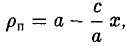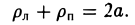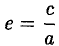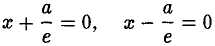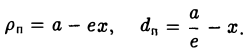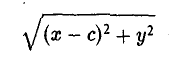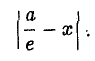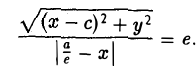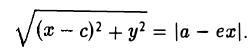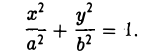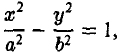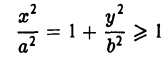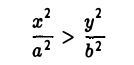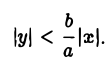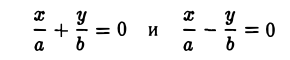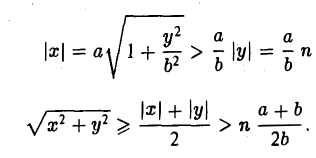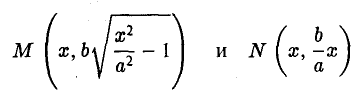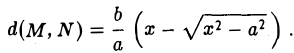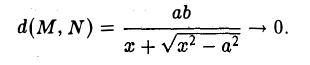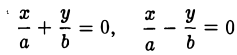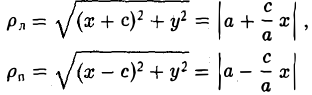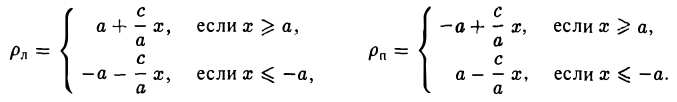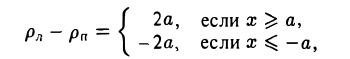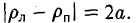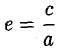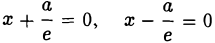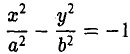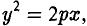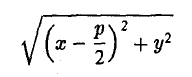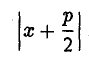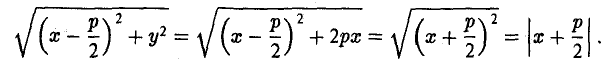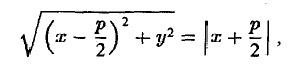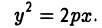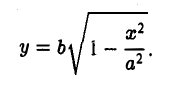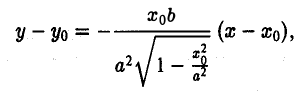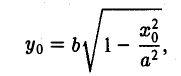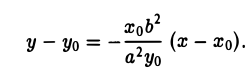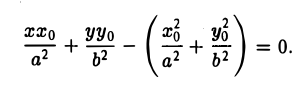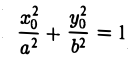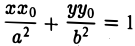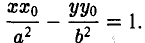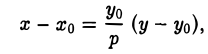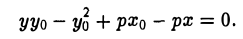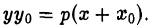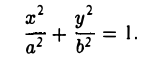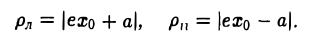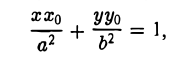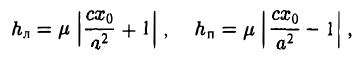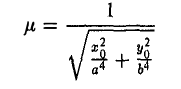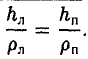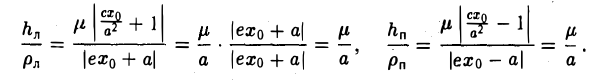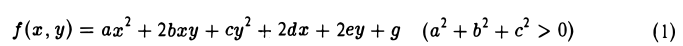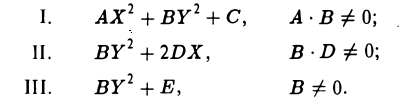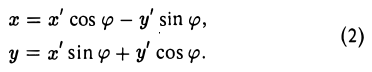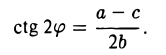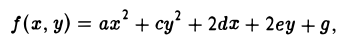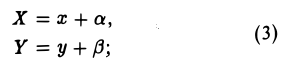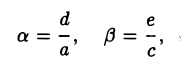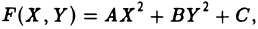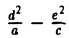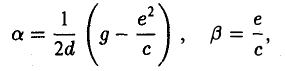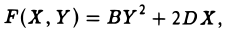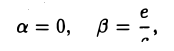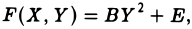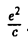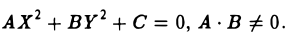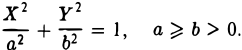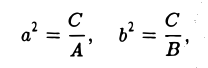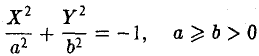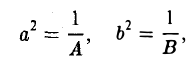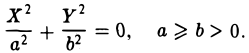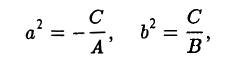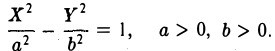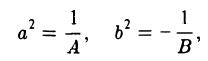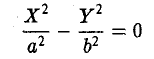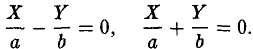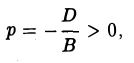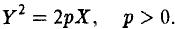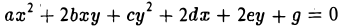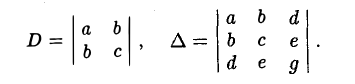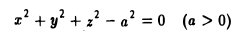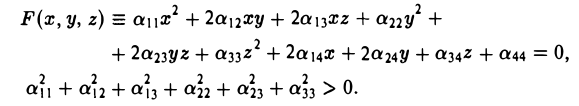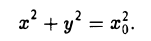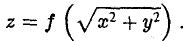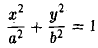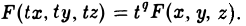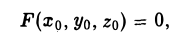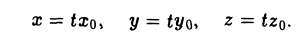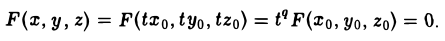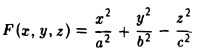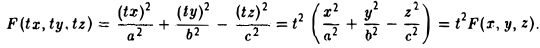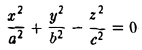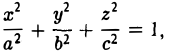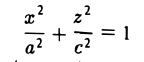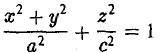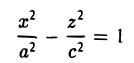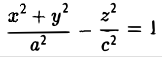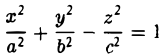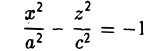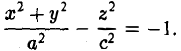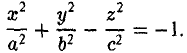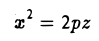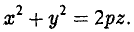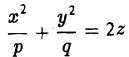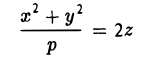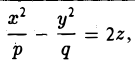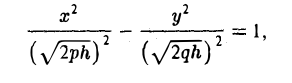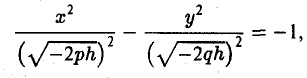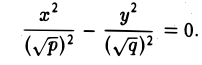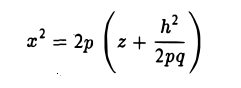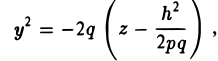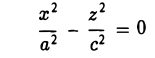- Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
- Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
- Эллипсоид
- Мнимый эллипсоид
- Мнимый конус
- Однополостный гиперболоид
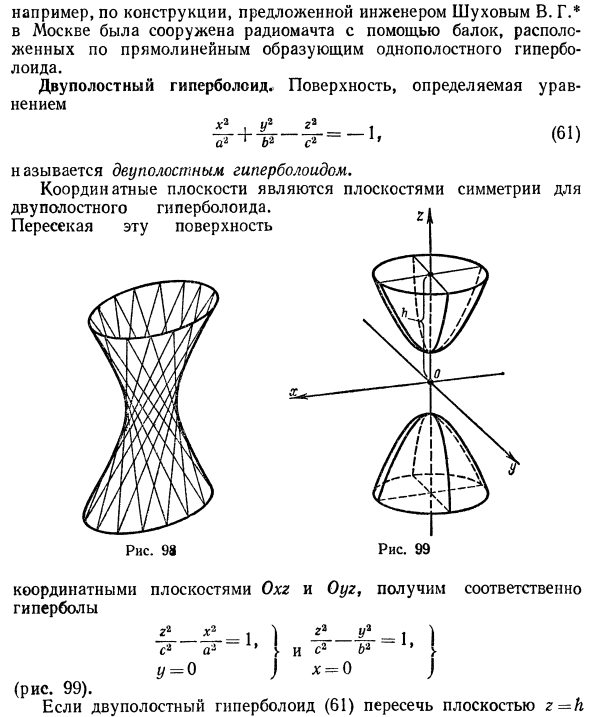
- Двуполостный гиперболоид
- Конус
- Эллиптический параболоид
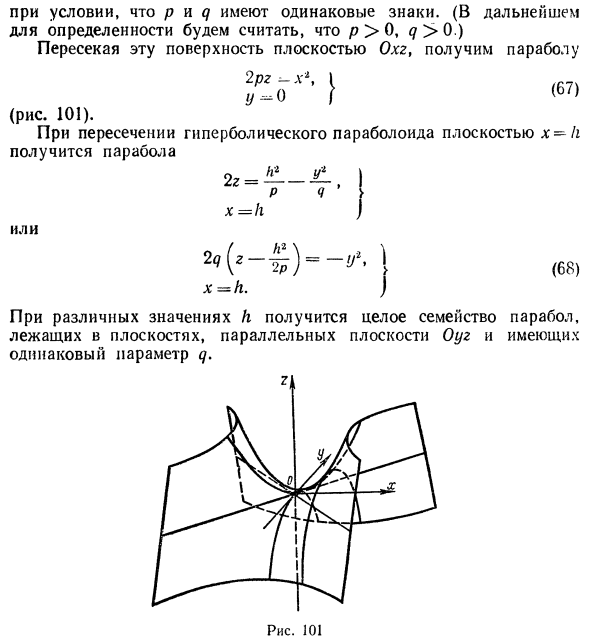
- Гиперболический параболоид
- Эллиптический цилиндр
- Мнимый эллиптический цилиндр
- Мнимые пересекающиеся плоскости
- Гиперболический цилиндр
- Пересекающиеся плоскости
- Параболический цилиндр
- Параллельные плоскости
- Мнимые параллельные плоскости
- Совпадающие плоскости
- Решение примеров на определение вида поверхности второго порядка
- Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
- Поверхности второго порядка
- Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения
- Кривые и поверхности второго порядка
- Преобразование координат на плоскости
- Параллельный перенос
- Поворот
- Зеркальное отражение
- Кривые второго порядка
- Эллипс
- Свойства эллипса
- Гипербола
- Свойства гиперболы
- Парабола
- Свойства параболы
- Оптическое свойство кривых второго порядка
- Касательные к эллипсу и гиперболе
- Касательные к параболе
- Оптическое свойство эллипса
- Оптическое свойство гиперболы
- Оптическое свойство параболы
- Классификация кривых второго порядка
- Многочлены второй степени на плоскости
- Канонические уравнения кривых второго порядка
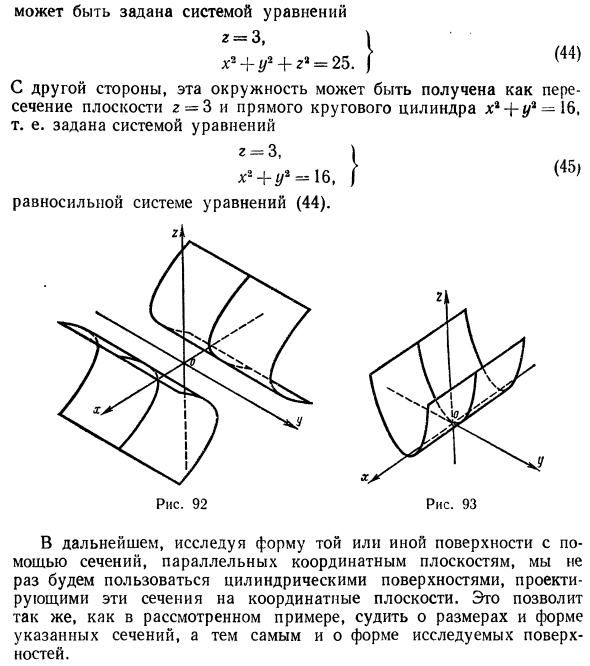
- Поверхности второго порядка
- Некоторые классы поверхностей
- Поверхности вращения
- Цилиндрические поверхности
- Конические поверхности
- Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка
- Эллипсоид
- Гиперболоиды
- Эллиптический параболоид
- Дополнение к поверхностям второго порядка
- 📸 Видео
Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут



Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:




Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:




Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:




то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая


получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем 



получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:


Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:


Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

перепишем его в виде

Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

перепишем его в виде

Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Видео:Поверхности второго порядкаСкачать
Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :

I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:






Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :


Следовательно, общее уравнение определяет эллиптический параболоид.

I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:





Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением



I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.


Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Видео:Пример определения кривой второго порядкаСкачать

Поверхности второго порядка
Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:
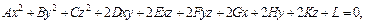
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.
1. Эллипсоид: 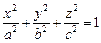
2. Конус второго порядка: 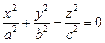
3. Гиперболоиды
1) однополостный: 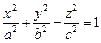 (рис. 15.3); (рис. 15.3); | 2) двуполостный: 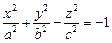 (рис. 15.4). (рис. 15.4). |
Рис. 15.3 Рис. 15.4
4. Параболоиды
1) эллиптический: 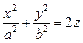 (рис. 15.5); (рис. 15.5); | 2) гиперболический: 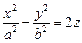 (рис.15.6). (рис.15.6). |
 |  |
Рис. 15.5 Рис. 15.6
5. Цилиндры
1) эллиптический: 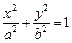 (рис. 15.7); (рис. 15.7); | 2) гиперболический: 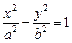 (рис. 15.8); (рис. 15.8); |
 |  |
Рис. 15.7 Рис. 15.8
3) параболический: 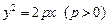
Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в общем уравнении поверхности коэффициенты 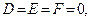
В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

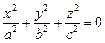
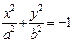
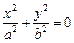
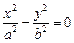
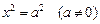
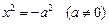

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:
1)
2)
3)
4)
Решение. 1) Воспользуемся методом выделения полных квадратов.
Преобразуем левую часть уравнения:
Значит, заданное уравнение равносильно уравнению
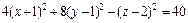
Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).
2) Поскольку
то заданное уравнение равносильно уравнению
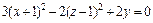
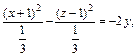
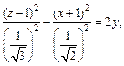
3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:
Поэтому заданное уравнение принимает вид:
или (после деления на 36)
Это уравнение эллипсоида с центром в точке (3, – 1, 2).
4. Методом выделения полных квадратов уравнение 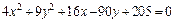
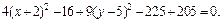
Почленное деление на 36 дает:
Это уравнение эллиптического цилиндра, смещенного в точку
(–2, 5, 0).
Пример 2. Исследовать поверхность методом сечений и построить ее:
Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.
Определим сечение поверхности плоскостями 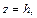
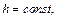
Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением
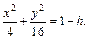
Уравнение (15.23) при 
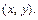
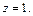
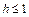
с полуосями 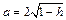
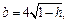
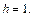
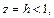
Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:
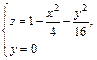
В первом случае имеем кривую 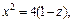
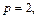
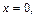
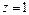
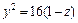
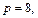
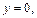
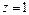
Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид 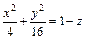
Пример 3. Построить тело, ограниченное поверхностями
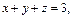
Решение. Уравнение 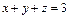
т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.
Уравнение 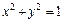
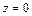
Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.
Видео:Определить тип кривой (эллипс)Скачать

Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Кривые и поверхности второго порядка
Преобразование координат на плоскости
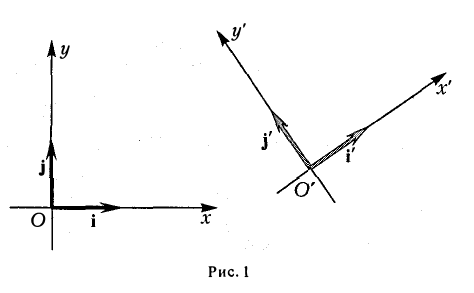
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.
Параллельный перенос
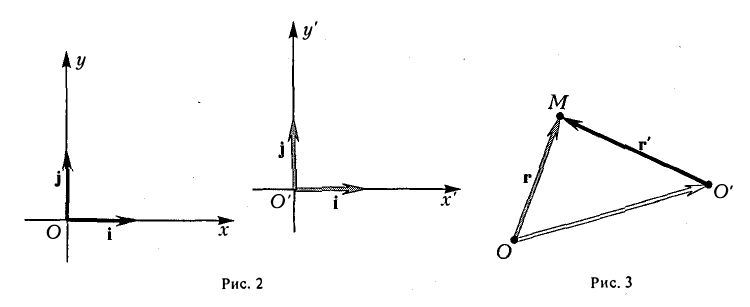
Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).
Пусть г и г’ — радиусы-векторы точки М, т.е.
и а, β — координаты точки О’ относительно системы координат Оху, т. е.
Поворот
Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и 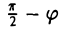
а координатами единичного вектора j’ служат косинусы углов 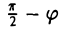
(рис. 5). Так как радиус-векторы
произвольной точки М в рассматриваемом случае равны,
то, заменяя векторы i’ и j’ их выражениями, получаем, что
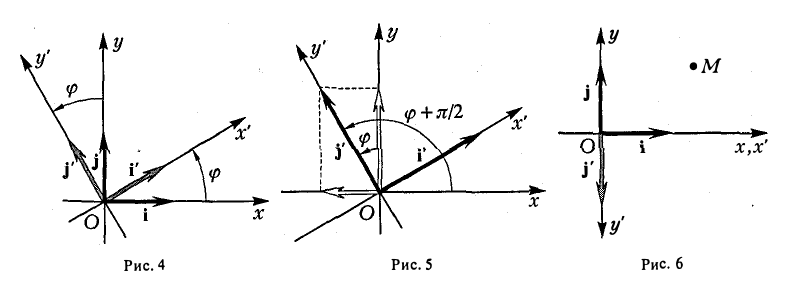
Зеркальное отражение
В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами
Справедливо следующее утверждение.
Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.
Кривые второго порядка
Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству
F(x, у) = 0,
где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).
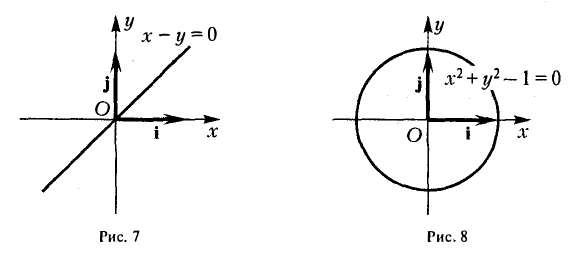
Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).
Рассмотрим многочлен второй степени от двух переменных х и у:
F(x,y) = 0
будем называть уравнением линии (кривой) второго порядка.
Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.
Эллипс
Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом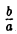
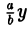
Свойства эллипса
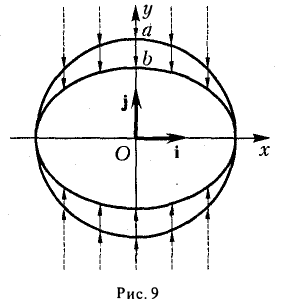
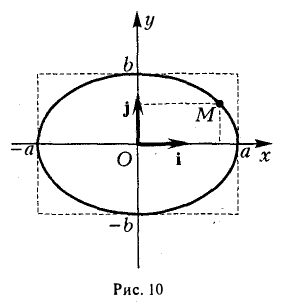
- Эллипс (I) содержится в прямоугольнике
В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)
Точки (±а, 0), (0, ±b) называются вершинами эллипса.
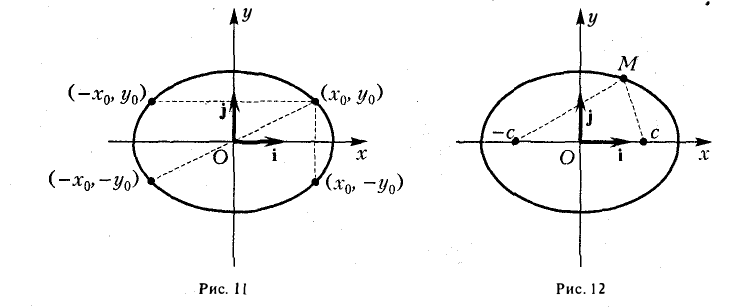
2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).
3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.
Положим с = 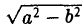
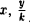
Пусть сначала М(х, у) — произвольная точка эллипса
Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем
Заменяя y 2 его выражением
после несложных преобразований получаем, что
Последнее равенство вытекает из того, что
Легко убедиться в том, что
Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).
называется эксцентриситетом эллипса (I). Ясно, что 0
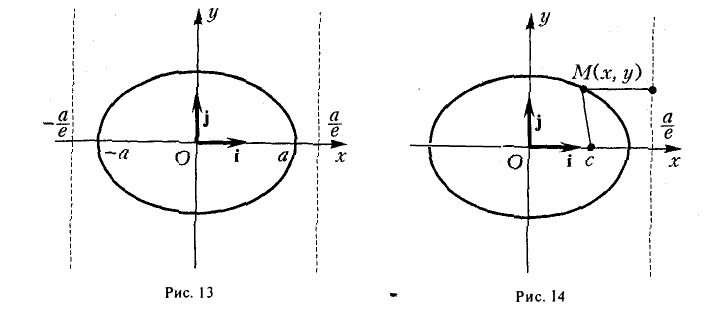
называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).
5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).
Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно
Откуда легко получаем требуемое
Аналогично проверяется, что
Рассмотрим теперь на плоскости точку (с, 0) и прямую х =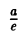
— и до выбранной прямой —
Возведем обе части последнего соотношения в квадрат и, положив 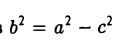
Тем самым, точка М(х,у) лежит на эллипсе (1).
Гипербола
Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.
Свойства гиперболы
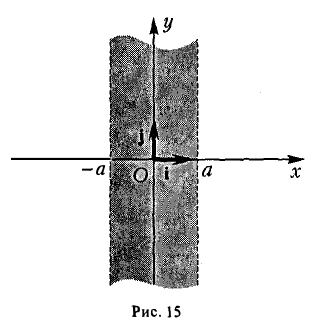
- Гипербола (1) лежит вне полосы |x|
и, значит, |x| ≥ а (рис. 15).
Точки (±а, 0) называются вершинами гиперболы.
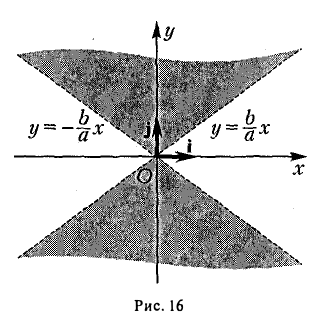
2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±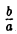
вытекает, что если точка М(х, у) лежит на гиперболе (1), то
Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые
называются асимптотами гиперболы.
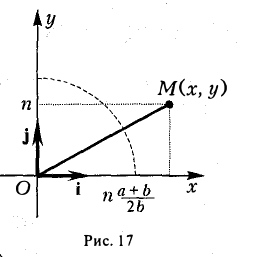
3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).
Пусть, например, точка М(х, у) лежит на гиперболе (1) и у = n, где n — произвольное положительное число (рис. 17).
Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты 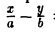
соответственно — и вычислим расстояние между ними. Имеем
Умножив и разделив полученное выражение на сумму х +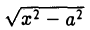
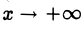
Тем самым, установлен следующий факт.
4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. х —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).
Верно и обратное.
стремится к нулю.
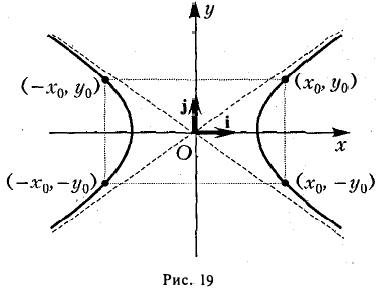
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).
Координатные оси канонической системы — единственные оси симметрии гиперболы.
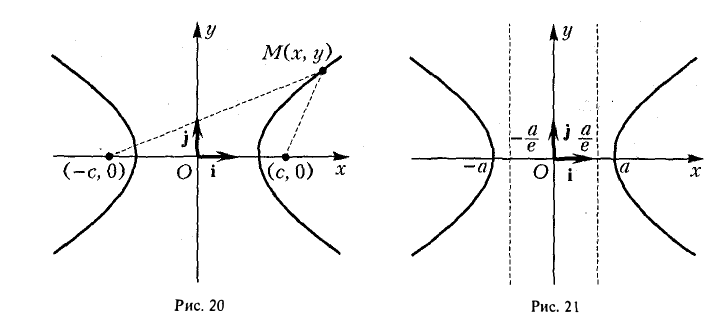
Положим с = 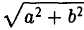
Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).
Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны
(рис. 20). Так как 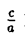
Отсюда нетрудно вычислить, что
называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые
называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.
Практически также, как и для эллипса, доказывается следующий факт.
8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
Гипербола (2)
называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.
Парабола
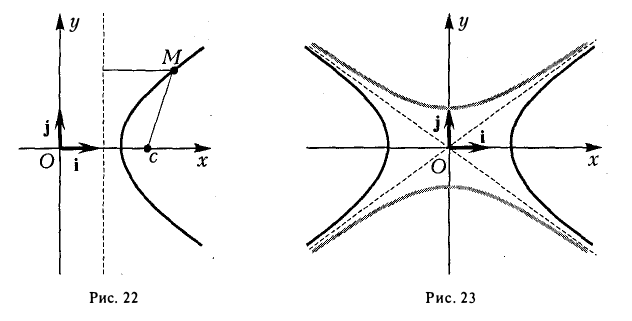
Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.
Свойства параболы
- Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
- На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
- Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).
Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (

4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).
Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (
и до директрисы х = —
Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что
Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (

то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:
Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Оптическое свойство кривых второго порядка
Касательные к эллипсу и гиперболе
Если кривая задана уравнением
y = f(x)
то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде
Пусть Мо(хо, yо) — точка эллипса
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением
Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо
а так как точка (х0, у о) лежит на эллипсе, то
Полученное соотношение после несложных преобразований можно записать так:
Отсюда с учетом тождества
приходим к уравнению
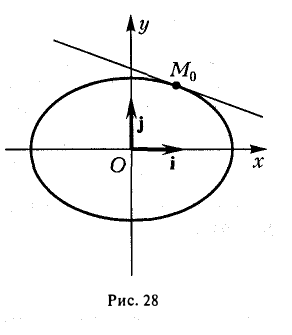
(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид
Подчеркнем, что точка (хо, yо) лежит на гиперболе.
Касательные к параболе
Если кривая задана уравнением
х = g(у),
то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде
Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе
Отсюда в силу равенства 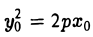
Замечание:
Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу 0 , а х 2 на хх 0 (в случае параболы 2х нужно заменить на x + х 0 ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x 0 . y 0 ) лежит на кривой.
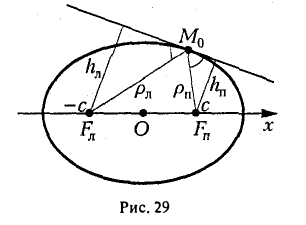
Оптическое свойство эллипса
Пусть М 0 — произвольная точка эллипса
Как уже отмечалось, расстояния от нее до фокусов Fл и F n — фокальные радиусы — равны соответственно
Проведем через точку М 0 касательную к эллипсу,
и вычислим, на каком расстоянии от этой касательной лежат фокусы Fл (-c, 0) и Fn (c; 0) (напомним, что для этого следует воспользоваться формулой (10).
— нормирующий множитель (рис. 29). Нетрудно проверить, что
Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.
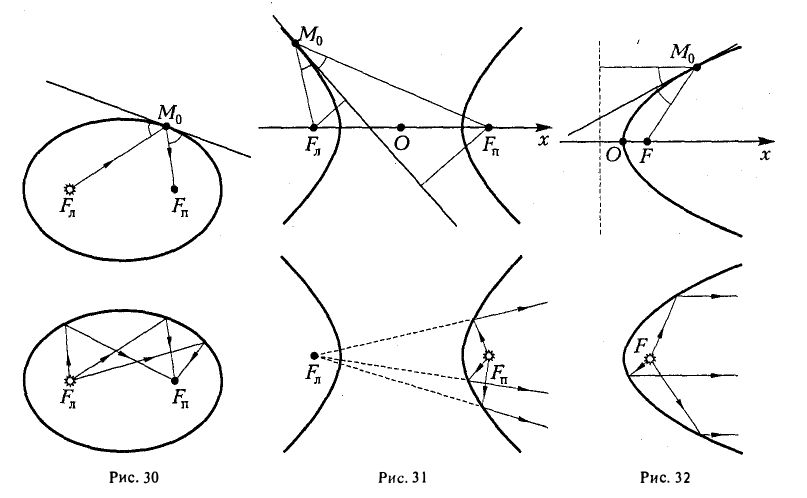
Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Оптическое свойство гиперболы
Устанавливается аналогичными выкладками и заключается в следующем.
Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).
Оптическое свойство параболы
Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Классификация кривых второго порядка
Многочлены второй степени на плоскости
Теорема:
Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть
— многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:
1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.
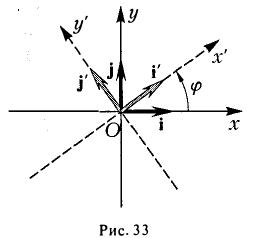
Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами
При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).
Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен
и обращается в нуль, если
Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид
где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).
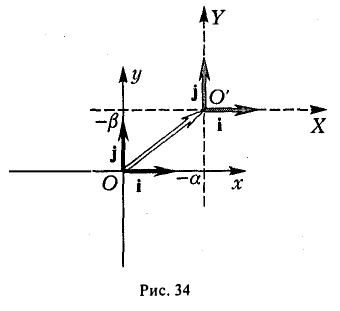
2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:
координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).
Укажем конкретные значения а и β. Возможны три случая
I. а ≠ 0, с ≠ 0. Тогда, полагая
где А = а, В = с, С = g —
II. а = 0, d ≠ 0. Тогда, полагая
III. а = d = 0. Тогда, полагая
где В = с, Е = g —
Канонические уравнения кривых второго порядка
Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка
F(X, У) = 0.
Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.
I.
Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.
- С
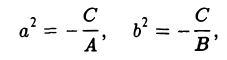
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.
Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).
Г. А • В 0, В
— пару пересекающихся прямых:
2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.
II. BY 2 + 2DX = О, В • D ≠ 0.
Всегда можно добиться того, чтобы В • D
III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.
1. Е
Y 2 — с 2 = 0, с > 0
— пару параллельных прямых.
Y 2 — с 2 = 0, с 2 = 0
— пара совпадающих прямых.
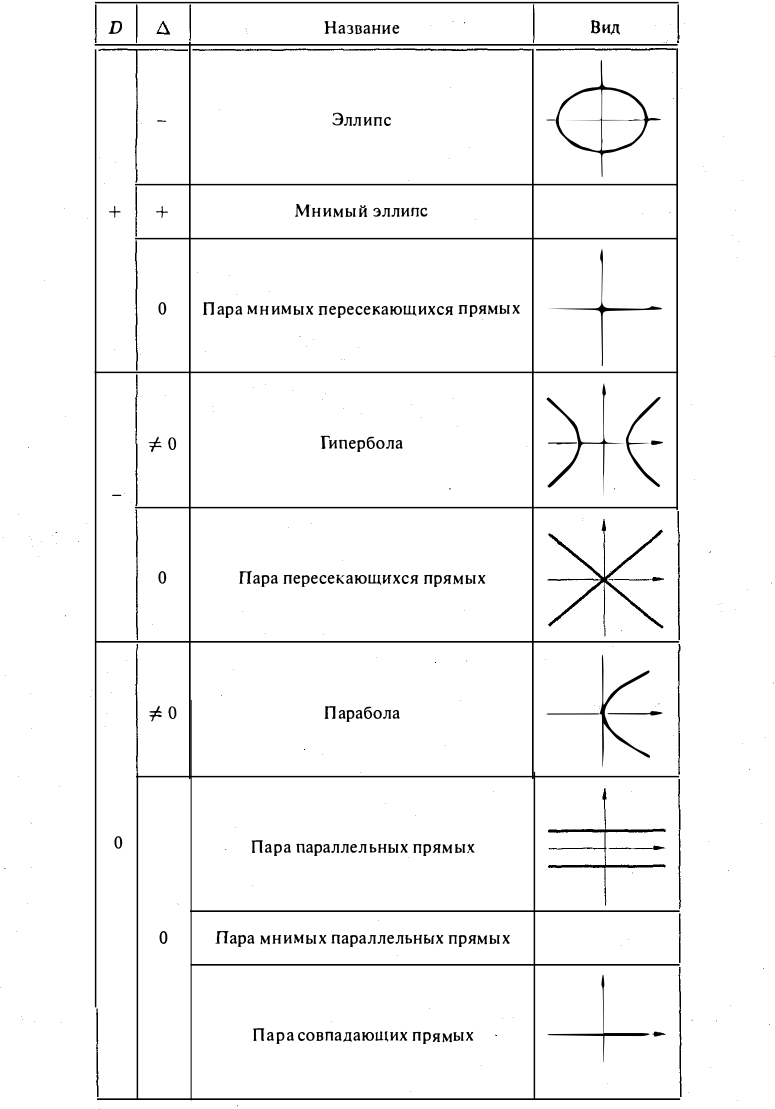
Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
— уравнение линии второго порядка. Введем следующие обозначения
Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.
Задача:
Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.
Поверхности второго порядка
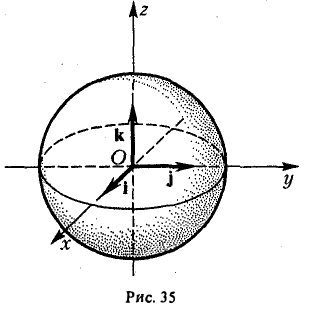
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству
F(x, у, z) = О,
называется поверхностью; равенство (*) называется уравнением этой поверхности.
Пример:
— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).
Рассмотрим многочлен второй степени от трех переменных х, у и z
Уравнение
F(x, y, z) = 0
будем называть уравнением поверхности второго порядка.
Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.
В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.
Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Некоторые классы поверхностей
Поверхности вращения
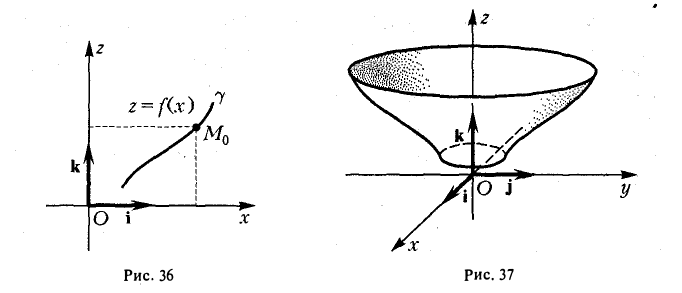
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением
г = f(x), х ≥ 0
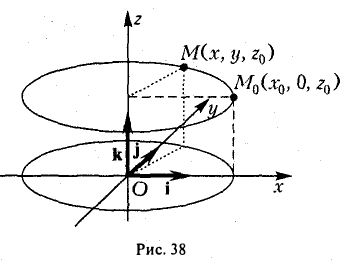
(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.
Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством
В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид
Цилиндрические поверхности
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.
Найдем уравнение, описывающее цилиндрическую поверхность.
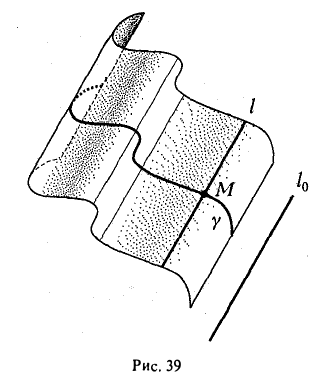
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.
F(x,y) = 0
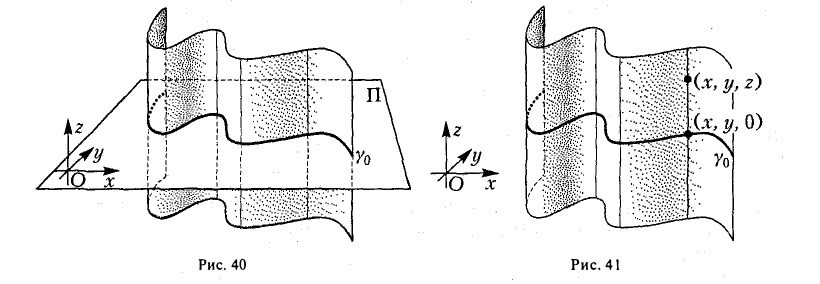
— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.
самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению
F(x,y)=0.
Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.
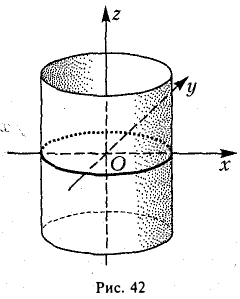
Пример:
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение
является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).
Замечание:
F(y, z) = 0
описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение
F(x,z) = 0
— цилиндрическую поверхность с образующей, параллельной оси Oy.
Конические поверхности
Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию
F (x, у, z)
переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство
Покажем, что если F(x, у, z) однородная функция, то F<x,y,z) = 0
является уравнением конической поверхности.
В самом деле, пусть
т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что 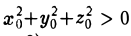
Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что
Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.
Пример:
является однородной функцией второй степени:
— уравнение конической поверхности (конуса второго порядка) (рис.45).
Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.
Видео:§21 Каноническое уравнение гиперболыСкачать

Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка
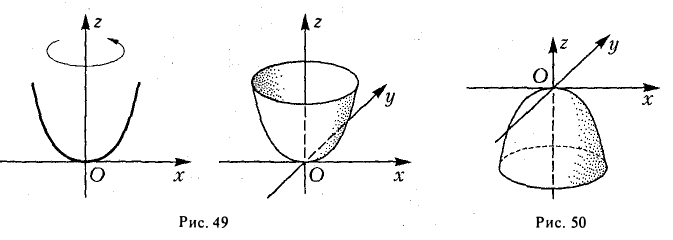
Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
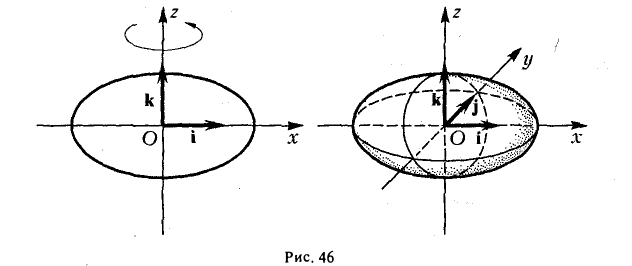
где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс
и будем вращать его вокруг оси Oz (рис. 46).
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — 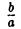
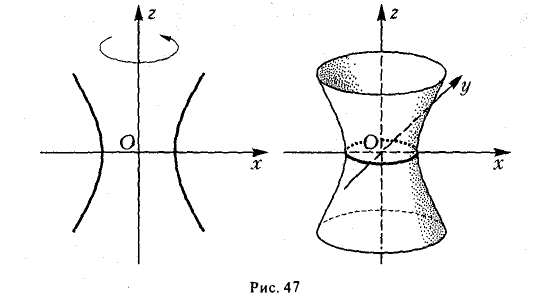
Гиперболоиды
вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид
получается тем же способом, что и в случае эллипсоида вращения.
5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — 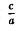
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 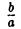
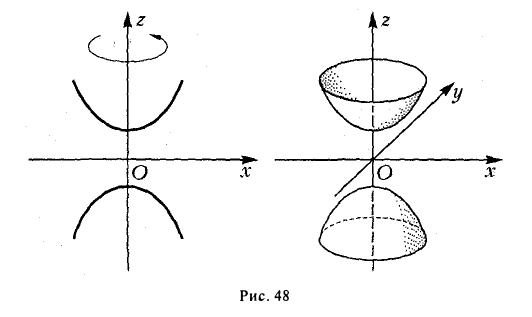
получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы
получим двуполостный гиперболоид вращения (рис.48). Его уравнение
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 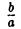
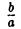
Эллиптический параболоид
вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид
Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом 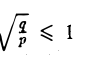
получается из уравнения параболоида вращения
путем замены у на 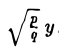
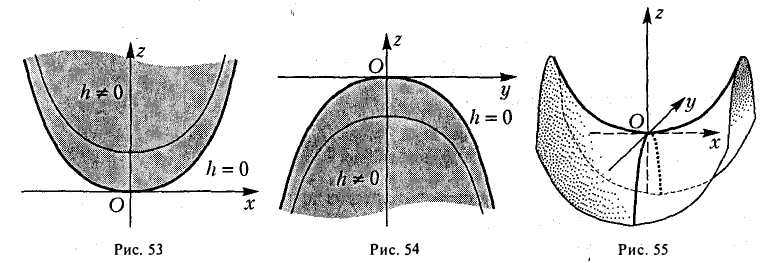
Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.
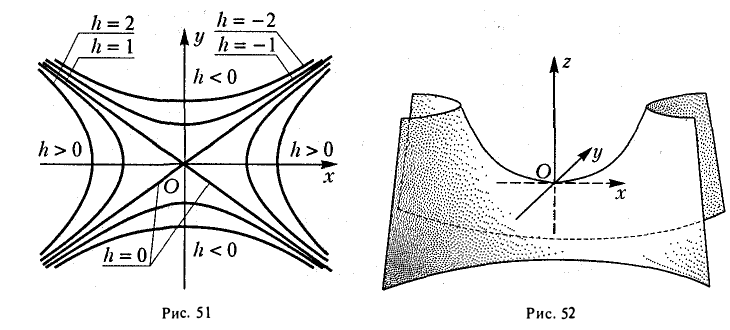
Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы
при h
при h = 0 — пару пересекающихся прямых
Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).
Рассмотрим теперь сечения плоскостями
у = h.
Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).
Аналогичная картина возникает при рассечении заданной поверхности плоскостями
х = h.
В этом случае также получаются параболы
ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).
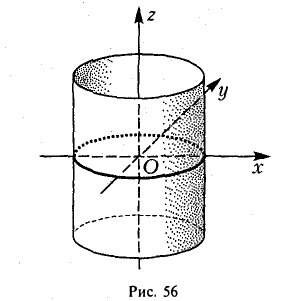
Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).
Замечание:
Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.
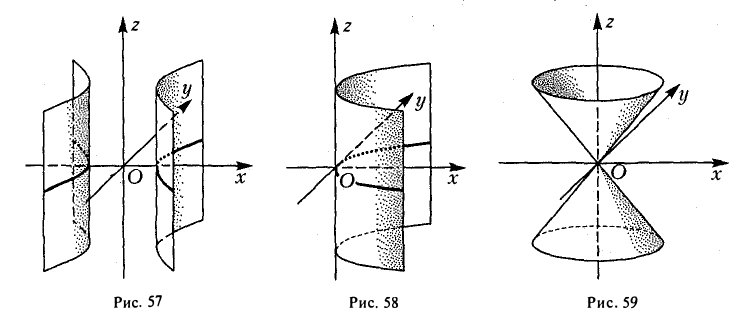
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:
представление о котором можно получить либо путем вращения пары пересекающихся прямых
вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.
Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Дополнение к поверхностям второго порядка





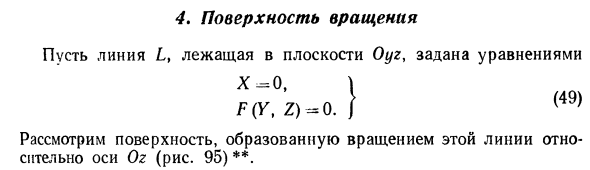




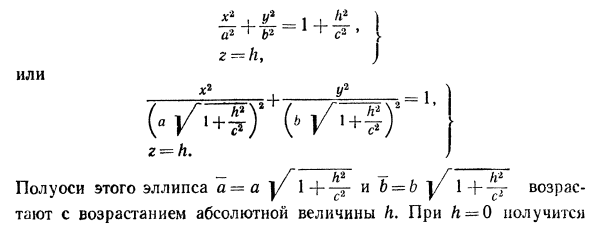

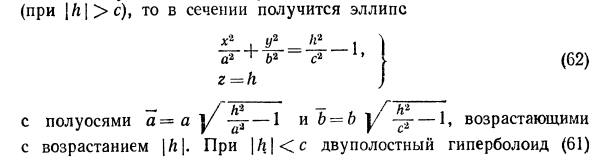


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📸 Видео
Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

ТФКП. Кривые в комплексной области. Определить вид кривой, заданной уравнением z(t)=x(t)+i·y(t)Скачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Семинар Аналитическая геометрия. Кривые и поверхности второго порядка.Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Тип кривой второго порядкаСкачать

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать