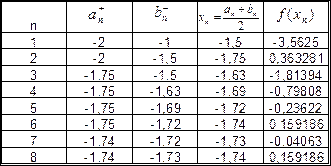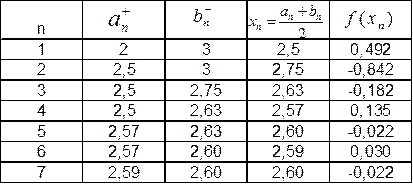Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).
4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.
Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.
Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;
Составим таблицу знаков функции f(x):
| x | -∞ | -1 | 3/4 | +∞ | |
| f(x) | + | — | — | — | + |
Из таблицы видно, что уравнение имеет два действительных корня x1 
(-∞;-1) и x2 (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:
| x | -2 | -1 | ||
| f(x) | + | — | — | + |
Следовательно, x1 (-2;-1) и x2 (1;2).
Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
Второй корень, уточняемый аналогичным образом, равен 1,73.
2. Отделить корни графически и уточнить их методом половинного деления.
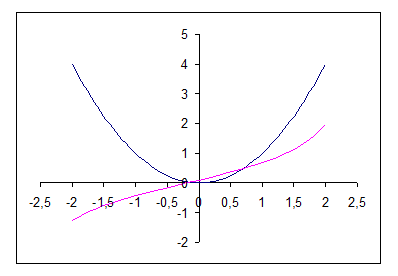
Перепишем уравнение в виде 
. Обозначим 
, 
и построим графики этих функций:
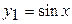
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].
Уточним корень на отрезке [2;3]:
Задания
1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.
1. 3x 4 +4x 3 -12x 2 -5=0
2. 2x 3 -9x 2 -60x+1=0
5. 3x 4 +3x 3 +6x 2 -10=0
7. x 4 +4x 3 -3x 2 -17=0
8. x 4 -x 3 -2x 2 +3x-3=0
9. 3x 4 +4x 3 -12x 2 +1=0
10. 3x 4 -8x 3 -18x 2 +2=0
11. 2x 4 -3x 3 +8x 2 -1=0
12. 2x 4 +8x 3 +3x 2 -1=0
13. x 4 -4x 3 -8x 2 +1=0
14. 3x 4 +4x 3 -12x 2 -5=0
15. 2x 3 -8x 2 -30x+1=0
17. 2x 4 -2x 2 -7=0
18. 3x 4 +8x 3 +6x 2 -10=0
19. x 4 -18x 2 +6=0
20. x 4 +4x 3 -3x-7=0
21. x 4 -2x 3 -x 2 +3x-3=0
22. 3x 4 +4x 3 -3x 2 -17=0
23. 2x 4 -5x 3 -12x 2 +2=0
24. 3x 4 +9x 3 -14x 2 +1=0
25. x 4 +2x 3 -x-1=0
26. x 4 +8x 3 -6x 2 -72x=0
28. x 4 -3x 2 +75x-10000=0
2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.
Лабораторная работа №3
Решение нелинейных уравнений методом хорд
Краткая теория
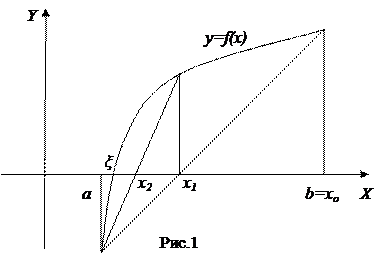
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):
Здесь ξ — точный корень уравнения (1), x 
— начальное приближение к корню, x 
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x 
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,
x 
=a- 
(2)
Для случая неподвижного конца b используется формула: x =a,
x =x 
— 
(3)
Правило определения неподвижного конца хорды:
Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.
Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 
1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.
2. Вычислить новое приближение к корню x по формуле (2) или (3).
3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2
Решение одного варианта
1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x 
.
Отделим корень графически. Построим графики функций
y =tg(0.5x+0.1) и y =x :
Таким образом, уравнение имеет два корня
x [0.5; 1] и x [-0.5; 0]
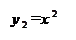
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем
f ‘(x)=0.5/cos (0.5x+0.1)-2x;
3. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. x lgx — 1.2 = 0
14. 1.8x 2 – sin10x = 0
15. ctgx – x / 4 = 0
16. tg(0.3x + 0.4) = x 2
17. x – 20sinx = 0
18. ctgx – x / 3 = 0
19. tg(0.47x + 0.2) = x 2
20. x 2 + 4sinx = 0
21. ctgx – x / 2 = 0
22. 2x – lgx – 7 = 0
24. 3x – cosx – 1 = 0
26. 10cosx-0,1x 2 =0
2)Отделить корни аналитически и уточнить их методом хорд до 0.001:
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Определить корни уравнения графически и уточнить один из них итерационным методом с точностью 0
№1. Определить корни уравнения графически и уточнить один из них итерационным методом с точностью 0,01. x3 +0,5x – 1=0 метод деления пополам.
Решение:
Определим корни уравнения графическим методом. Для этого построим график функции fx=x3+0.5x-1.
По чертежу видно, что корень уравнения x3+0.5x-1=0 расположен в диапазоне 0.5 ε
Шаг 2. a1;b1=[0.75;1]. x2=a1+b12=0.75+12=1.752=0.875.
Так как fa1=f0.75=-0.203, fx2=f0.875=0.107, fb1=f1=0.5 то полагаем
a2=0.75, b2=0.875, d2=b2-a2=0.125>ε
Шаг 3. a2;b2=[0.75;0.875]. x3=a2+b22=0.75+0.8752=1.6252=0.8125.
Так как fa2=f0.75=-0.203, fx3=f0.8125=-0.057, fb1=f0.875=0.107 то полагаем
a3=0.8125, b3=0.875, d3=b3-a3=0.06>ε
Шаг 4. a3;b3=[0.8125;0.875]. x4=a2+b22=0.8125+0.8752=1.68752=0.84375.
Так как fa3=f0.8125=-0.057, fx4=f0.84375=0.22, fb3=f0.875=0.107 то полагаем
a4=0.8125, b4=0.84375, d4=b4-a4=0.03>ε
Шаг 5. a4;b4=[0.8125;0.84375]. x5=a2+b22=0.8125+0.843752=1.656252=0.828125.
Так как fa4=f0.8125=-0.057, fx5=f0.828125=-0.02, fb4=f0.84375=0.22 то полагаем
a5=0.828125, b5=0.84375, d5=b5-a5=0.02>ε
Шаг 6. a5;b5=[0.828125;0.84375]. x6=a2+b22=0.828125+0.843752=1.6718752=0.8359375.
Так как fa5=f0.828125=-0.02, fx6=f0.8359375=0.002,
fb5=f0.84375=0.22 то полагаем
a6=0.828125, b6=0.8359375, d6=b6-a6=0.007
Ksunya266 4.3
Высшее образование в направлении менеджмент. Среднее специальное — государственное и муниципальное управление. В школе училась хорошо. Разбираюсь в большей части предметов начиная со школьных и заканчивая профильными.Буду рада Вам помочь!
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать
На каждый день | Алгебра
- Аналитическая геометрия (11 записей)
- Тригонометрия (10 записей)
- Справочник-словарь (28 записей)
- Проектировщику (231 записей)
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
СТЕПЕНИ И КОРНИ
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать
ЛОГАРИФМЫ
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать
ПРОГРЕССИИ
Видео:Графический метод решения уравнений 8 классСкачать
ФАКТОРИАЛ
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
СОЕДИНЕНИЯ
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать
БИНОМ НЬЮТОНА
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
ОПРЕДЕЛИТЕЛИ (ДЕТЕРМИНАНТЫ)
Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать
УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ
2007-2020 © baurum.ru
All rights reserved.
Строительство и ремонт
О строительстве — для строителей, застройщиков,
заказчиков, проектировщиков, архитекторов
💥 Видео
Решение биквадратных уравнений. 8 класс.Скачать
Отбор корней по окружностиСкачать
Метод касательных (метод Ньютона)Скачать
СЛОЖИТЕ ДВА КОРНЯСкачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Как решают уравнения в России и СШАСкачать
Решение квадратных неравенств графическим методом. 8 класс.Скачать
Алгебра 9 класс. Графическое решение систем уравненийСкачать
