Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции — теория, практика, задачи.
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Книги — разная литература по теме.
Базовый курс лекций по сопромату, теория, практика, задачи.
4. Изгиб. определение перемещений.
4.1. Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки.
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):
.
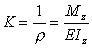
В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,
.
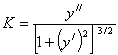
Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем
.
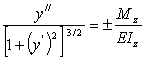
Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки
.
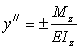
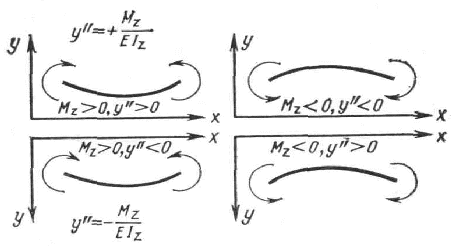
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений
,
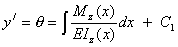
а после второго интегрирования – прогибы балки
.
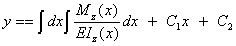
Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Метод непосредственного интегрирования
Этот метод сводится к интегрированию дифференциального уравнения изогнутой оси балки (9.1) при известном законе изменения изгибающих моментов М (х). Считая жесткость балки при изгибе постоянной (EJz = const) и последовательно интегрируя уравнение (9.1), получим
В выражениях (9.5) и в дальнейшем для упрощения записи опущены индексы у моментов инерции и изгибающих моментов.
Выражения (9.5) позволяют получить аналитические законы изменения прогибов и углов поворота в балке. Входящие в (9.5) постоянные интегрирования С1 и С2 подлежат определению из кинематических граничных условий и условий сопряжения участков балки.
Кинематические граничные условия отражают характер закрепления (опирания) балки и ставятся относительно прогибов и углов поворота. Например, для шарнирно опертой балки (рис. 9.4) граничные условия характеризуют отсутствие прогибов на опорах: х = 0, х = /, v = 0. Для консольной балки (рис. 9.5) граничные условия характеризуют равенство нулю прогиба и угла поворота в жесткой заделке: х = 0, v = 0; ср = 0.
Условия сопряжения ставятся на границах участков с различными законами изменения изгибающих моментов. При отсутствии промежуточных шарниров и так называемых параллелограммных механизмов (ползунов) условия сопряжения заключаются в равенстве прогибов и углов поворота в сечениях слева и справа от границы участков, то есть они характеризуют непрерывность и гладкость изогнутой оси балки. Например, для балки на рис. 9.4 можно записать: х = а, и = и • 2 и модуль упругости стали Е— 2,1 • 10 4 кН/см 2 .
Принимаем 120, Wz = 184 см 3 , J = 1840 см 4 .
Вычислим наибольшие значения угла поворота и прогиба в балке. Согласно СНиП расчет производим на действие нормативных нагрузок.
Из рассмотренного примера видно, что при наличии в балке нескольких участков с различными законами изменения изгибающих моментов метод непосредственного интегрирования становится громоздким и неудобным.
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Метод интегрирования дифференциального уравнения изгиба балки
Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.
$EI,y»(x) = M(x)$ – полученное дифференциальное уравнение;
$EI,y'(x) = EI,varphi (x) = int dx + C$ – первый интеграл (уравнение углов поворота);
$EI,y(x) = int dx = iint dxdx + C,x + D$ – второй интеграл (уравнение прогибов).
Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).
Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI,varphi (0) = C$, а прогиб $EI,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
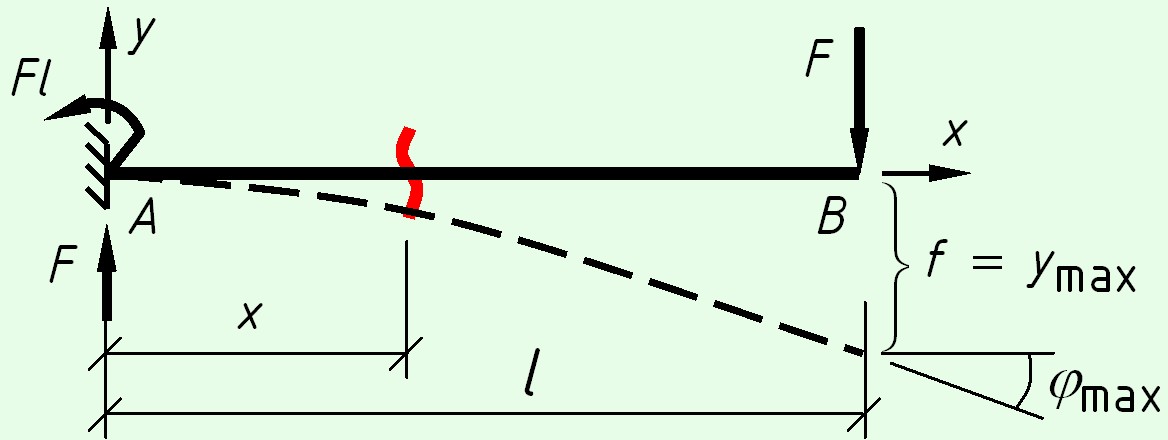
Консольная балка с силой на конце
На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F cdot l$.
Уравнения изгибающих моментов
$M(x) = — Fl + Fx = F(x — l)$
Уравнение углов поворота
$EI,y'(x) = EI,varphi (x) = int dx + C = F(frac<<>> — lx) + C$
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$left < beginEI,varphi (0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$
Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = frac<<F,>><>$.
Максимальный угол поворота сечения также будет иметь место при $x = l$
знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
Шарнирно закрепленная балка с силой посередине
На опорах возникают вертикальные реакции $ = = F/2$.
Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид
$M(x) = fracx$, то есть $EI,y»(x) = fracx$, интегрируем дважды
Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l/2$
Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).
Видео:Дифференциальные уравнения. 11 класс.Скачать
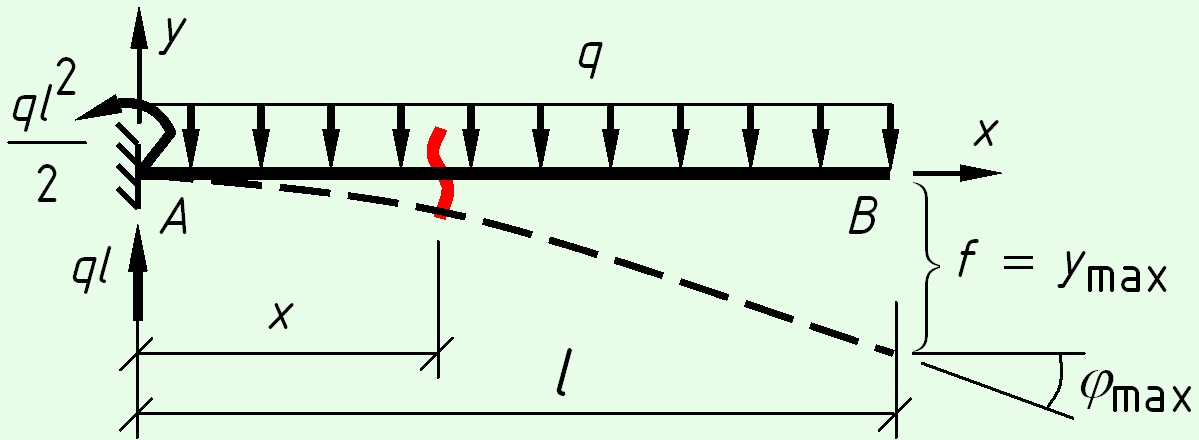
Консольная балка с равномерно распределенной нагрузкой
На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = frac<<q>>$.
$M(x) = — frac<<q>> + ql cdot x — frac<<q>>$, дважды интегрируем
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$left < beginEI,y'(0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$
Решение системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
Максимальный прогиб будет иметь место при $x = l$
Максимальный угол поворота сечения также будет иметь место при $x = l$
📽️ Видео
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
Решение системы дифференциальных уравнений методом ЭйлераСкачать
Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
Простейшие дифференциальные уравненияСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
