Две системы линейных уравнений от одного набора x1. xn неизвестных и соответственно из m и p уравнений
называются эквивалентными, если их множества решений 


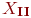





Элементарные преобразования систем линейных уравнений (строк матриц)
Определение 3.4.1 (элементарное преобразование 1-го типа). При 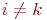

т. е. в новом i -м уравнении aij’=aij+cakj, bi’=bi+cbk.
Определение 3.4.2 (элементарное преобразование 2-го типа). При 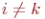
| 53. Метод Гаусса решения систем линейных уравнений | |||||||||||||||||||||
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме. Для того чтобы решить систему уравнений выписывают расширенную матрицу этой системы 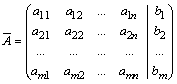 и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы  будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему 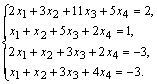 Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент 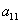 равнялся единице (так удобнее производить преобразования матрицы). равнялся единице (так удобнее производить преобразования матрицы). 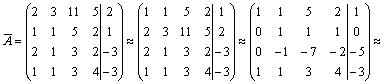  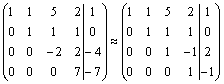 . Имеем . Имеем  Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:  Итак, имеем Итак, имеем  Далее, подставляя Далее, подставляя  в третье уравнение, найдем в третье уравнение, найдем  Подставляя Подставляя  и и 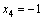 во второе уравнение, получим во второе уравнение, получим  и, наконец, подставляя в первое уравнение найденные и, наконец, подставляя в первое уравнение найденные  получим получим  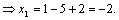 Таким образом, имеем решение системы Таким образом, имеем решение системы  54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида 54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида
Эта система может быть записана в виде матричного уравнения и операторного уравнения
Система (1) всегда совместна, так как: имеет очевидное решение x10 = x20 = … = xn0 = 0 , которое называется нулевым, или тривиальным; добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли; θ О Img ^A , так как Img ^A — линейное пространство. Естественно, нас интересуют нетривиальные решения однородной системы. Условие нетривиальной совместности: Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных. Доказательство см. в книге О.В. Зиминой «Линейная алгебра и аналитическая геометрия», стр. 77. Следствие. Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det A = 0 ). Общим решением системы линейных уравнений называется формула, которая определяет любое ее решение. Так как система (1) эквивалентна операторному уравнению (2), то множество всех ее решений есть ядро оператора ^A . Пусть Ker ^A ≠ θ , Rg ^A = r и x1, x2, … , xn − r — базис в ядре оператора. Фундаментальной системой решений однородной системы (1) называется базис ядра оператора ^A (точнее, координатные столбцы базисных векторов в Ker ^A ). Это определение можно сформулировать несколько иначе: Фундаментальной системой решений однородной системы (1) называется n − r линейно независимых решений этой системы. Будем обозначать координатные столбцы базисных векторов в Ker ^A X1, X2, … , Xn − r . Теорема о структуре общего решения однородной системы уравнений: Любое решение однородной системы линейных уравнений определяется формулой
где X1, X2, … , Xn − r — фундаментальная система решений однородной системы линейных уравнений и C1, C2, … , Cn − r — произвольные постоянные. Свойства общего решения однородной системы уравнений: При любых значениях C1, C2, … , Cn − r X , определяемое формулой (3), является решением системы (1). Каково бы ни было решение X0 , существуют числа C10, … , Cn − r0 такие, что
Вывод: Чтобы найти фундаментальную систему и общее решение однородной системы, нужно найти базис ядра соответствующего линейного оператора. Содержание Видео:Билет 2 (Элементарные преобразования, эквивалентность, метод Гаусса)Скачать  Эквивалентность СЛАУ при элементарных преобразованияхОпределения Система m линейных уравнений с n неизвестными(или, линейная система) в линейной алгебре — это система уравнений вида
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Система (1) называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества. Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система вида (1) может иметь одно или более решений. Решения c1 (1) , c2 (1) , …, cn (1) и c1 (2) , c2 (2) , …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой. Матричная форма Система линейных уравнений может быть представлена в матричной форме как: или, согласно правилу перемножения матриц, Методы решения системы (1) Прямые методы § Метод прогонки — Для трехдиагональных матриц Приближенные методы § Метод Якоби (метод итераций) Метод Крамера (Крамера правило) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причем для таких уравнений решение существует и единственно). Описание метода Для системы с определителем матрицы системы (i-й столбец матрицы системы заменяется столбцом свободных членов). Рангом матрицы A называется наибольший из порядков миноров матрицы A , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Алгоритм вычисления ранга матрицы:
Свойства ранга матрицы:
Элементарные преобразования матрицы. Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду. Определение Элементарными преобразованиями строк называют: § перестановка местами любых двух строк матрицы; § умножение любой строки матрицы на константу § прибавление к любой строке матрицы другой строки, умноженной на константу Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования обратимы. Обозначение Свойства Инвариантность ранга при элементарных преобразованиях
Эквивалентность СЛАУ при элементарных преобразованиях Назовём элементарными преобразованиями над системой линейных алгебраических уравнений: § умножение уравнения на ненулевую константу; § сложение одного уравнения с другим, умноженным на некоторую константу. Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
Напомним, что две системы называются эквивалентными, если множества их решений совпадают. Видео:Эквивалентные системы линейных уравнений | Системы уравнений | Алгебра I (9 видео)Скачать  Понимание эквивалентных уравнений в алгебреПонимание эквивалентных уравнений в алгебре — Науки Видео:Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать  Содержание:Эквивалентные уравнения — это системы уравнений, которые имеют одинаковые решения. Выявление и решение эквивалентных уравнений — ценный навык не только на уроках алгебры, но и в повседневной жизни. Взгляните на примеры эквивалентных уравнений, как решить их для одной или нескольких переменных и как вы можете использовать этот навык за пределами классной комнаты. Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать  Ключевые выводы
Видео:7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать  Линейные уравнения с одной переменнойВ простейших примерах эквивалентных уравнений нет переменных. Например, эти три уравнения эквивалентны друг другу:
Признать, что эти уравнения эквивалентны, — это здорово, но не особенно полезно. Обычно задача эквивалентного уравнения просит вас решить для переменной, чтобы убедиться, что она такая же (та же корень) как одно в другом уравнении. Например, следующие уравнения эквивалентны: В обоих случаях x = 5.Откуда нам это знать? Как вы решите это для уравнения «-2x = -10»? Первый шаг — узнать правила эквивалентных уравнений:
Видео:Исследование систем линейных уравнений на совместностьСкачать  примерПрименяя эти правила на практике, определите, эквивалентны ли эти два уравнения:
Чтобы решить эту проблему, вам нужно найти «x» для каждого уравнения. Если «x» одинаково для обоих уравнений, то они эквивалентны. Если «x» отличается (т.е. уравнения имеют разные корни), то уравнения не эквивалентны. Для первого уравнения:
Для второго уравнения:
Итак, да, два уравнения эквивалентны, потому что x = 5 в каждом случае. Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать  Практические эквивалентные уравненияВы можете использовать эквивалентные уравнения в повседневной жизни. Это особенно полезно при покупках. Например, вам нравится определенная рубашка. Одна компания предлагает рубашку за 6 долларов с доставкой за 12 долларов, в то время как другая компания предлагает рубашку за 7,50 долларов с доставкой за 9 долларов. Какая рубашка имеет лучшую цену? Сколько рубашек (может быть, вы хотите подарить друзьям) вам придется купить, чтобы цена была одинаковой для обеих компаний? Чтобы решить эту проблему, пусть x будет числом рубашек. Для начала установите x = 1 для покупки одной рубашки. Для компании №1:
Итак, если вы покупаете одну рубашку, вторая компания предлагает более выгодную сделку. Чтобы найти точку, в которой цены равны, оставьте «x» числом рубашек, но приравняйте два уравнения друг к другу. Чтобы узнать, сколько рубашек вам нужно купить, решите для «x»:
Если вы покупаете две рубашки, цена будет одинаковой, независимо от того, где вы ее купите. Вы можете использовать ту же математику, чтобы определить, какая компания предлагает вам более выгодную сделку с крупными заказами, а также рассчитать, сколько вы сэкономите, используя одну компанию по сравнению с другой. Видите ли, алгебра полезна! Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать  Эквивалентные уравнения с двумя переменнымиЕсли у вас есть два уравнения и две неизвестные (x и y), вы можете определить, эквивалентны ли два набора линейных уравнений. Например, если вам даны уравнения: Вы можете определить, эквивалентна ли следующая система: Чтобы решить эту проблему, найдите «x» и «y» для каждой системы уравнений. Если значения совпадают, то системы уравнений эквивалентны. Начнем с первого подхода. Чтобы решить два уравнения с двумя переменными, выделите одну переменную и подставьте ее решение в другое уравнение. Чтобы изолировать переменную «y»:
Теперь вставьте «y» обратно в любое уравнение, чтобы найти «x»: Проработав это, вы в конечном итоге получите x = 7/3. Чтобы ответить на вопрос, вы мог примените те же принципы ко второму набору уравнений, чтобы решить для «x» и «y», чтобы обнаружить, что да, они действительно эквивалентны. В алгебре легко увязнуть, поэтому неплохо проверить свою работу с помощью онлайн-программы для решения уравнений. Однако умный ученик заметит, что две системы уравнений эквивалентны без каких-либо сложных вычислений. Единственная разница между первым уравнением в каждом наборе состоит в том, что первое в три раза больше второго (эквивалентного). Второе уравнение точно такое же. 📸 ВидеоРешение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать  ФСР системы линейных уравнений. Алгоритм ГауссаСкачать  Система линейных уравнений. Общее решение. Метод ГауссаСкачать  Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать  15. Однородная система линейных уравнений / фундаментальная система решенийСкачать  Математика без Ху!ни. Метод Гаусса.Скачать  Линейное уравнение с двумя переменными. 7 класс.Скачать  Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать  Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать  Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать  5 способов вычисления определителя ★ Какой способ лучше?Скачать  Решение системы уравнений методом ГауссаСкачать  |



 Править
Править
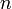 линейных уравнений с
линейных уравнений с 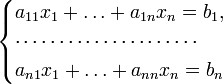
 , отличным от нуля, решение записывается в виде:
, отличным от нуля, решение записывается в виде: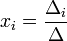 ,
, .
. ,
,  ;
; указывает на то, что матрица
указывает на то, что матрица  может быть получена из
может быть получена из 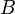 путём элементарных преобразований (или наоборот).
путём элементарных преобразований (или наоборот). .
.