Описать класс представляющий нелинейное уравнение вида ax cos x 0

При создании класса, то есть нового типа данных, следует хорошо продумать его интерфейс – средства работы с классом, доступные использующим его программистам. Интерфейс хорошо спроектированного класса интуитивно ясен, непротиворечив и обозрим. Как правило, он не должен включать поля данных.

Поля предпочтительнее делать закрытыми (private). Это дает возможность впоследствии изменить реализацию класса без изменений в его интерфейсе, а также регулировать доступ к полям класса с помощью набора предоставляемых пользователю свойств и методов. Важно помнить, что поля класса вводятся только для того, чтобы реализовать характеристики класса, представленные в его интерфейсе с помощью свойств и методов.

Не нужно расширять интерфейс класса без необходимости, ≪на всякий случай≫, поскольку увеличение количества методов затрудняет понимание класса пользователем. В идеале интерфейс должен быть полным, то есть предоставлять возможность выполнять любые разумные действия с классом, и одновременно минимально необходимым – без дублирования и пересечения возможностей методов.

Методы определяют поведение класса. Каждый метод класса должен решать только одну задачу (не надо объединять два коротких независимых фрагмента кода в один метод). Размер метода может варьироваться в широких пределах, все зависит от того, какие функции он выполняет. Желательно, чтобы тело метода помещалось на 1-2 экрана: одинаково сложно разбираться в программе, содержащей несколько необъятных функций, и в россыпи из сотен единиц по несколько строк каждая.

Если метод реализует сложные действия, следует разбить его на последовательность шагов и каждый шаг оформить в виде вспомогательной функции (метода со спецификатором private). Если некоторые действия встречаются в коде хотя бы дважды, их также нужно оформить в виде отдельной функции.

Создание любой функции следует начинать с ее интерфейса, то есть заголовка. Необходимо четко представлять себе, какие параметры функция должна получать и какие результаты формировать. Входные параметры обычно перечисляют в начале списка параметров.

Предпочтительнее, чтобы каждая функция вычисляла ровно один результат, однако это не всегда оправдано. Если величина вычисляется внутри функции и возвращается из нее через список параметров, необходимо использовать перед соответствующим параметром ключевое слово out. Если параметр значимого типа может изменить свою величину внутри функции, его предваряют ключевым словом ref. Величины ссылочного типа всегда передаются по адресу и, следовательно, могут изменить внутри функции свое значение.

Необходимо стремиться к максимальному сокращению области действия каждой переменной, то есть к реализации принципа инкапсуляции. Это упрощает отладку программы, поскольку ограничивает область поиска ошибки. Следовательно, величины, используемые только в функции, следует описывать внутри нее как локальные переменные.

Поля, характеризующие класс в целом, то есть имеющие одно и то же значение для всех экземпляров, следует описывать как статические. Все литералы, связанные с классом (числовые и строковые константы), описываются как поля-константы с именами, отражающими их смысл.

Каждый разрабатываемый класс должен, как правило, содержать следующие элементы: скрытые поля, конструкторы с параметрами и без параметров, методы, свойства. Методы и свойства должны обеспечивать непротиворечивый, полный, минимальный и удобный интерфейс класса. При возникновении ошибок должны выбрасываться исключения.

В программе должна выполняться проверка всех разработанных элементов класса.

Вариант 1

Описать класс, реализующий шестнадцатеричный счетчик, который может увеличивать или уменьшать свое значение на единицу в заданном диапазоне. Предусмотреть инициализацию счетчика значениями по умолчанию и произвольными значениями. Счетчик имеет два метода: увеличения и уменьшения, – и свойство, позволяющее получить его текущее состояние. При выходе за границы диапазона выбрасываются исключения.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 2

Описать класс, реализующий десятичный счетчик, который может увеличивать или уменьшать свое значение на единицу в заданном диапазоне. Предусмотреть инициализацию счетчика значениями по умолчанию и произвольными значениями. Счетчик имеет два метода: увеличения и уменьшения, – и свойство, позволяющее получить его текущее состояние. При выходе за границы диапазона выбрасываются исключения.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 3

Описать класс, представляющий треугольник. Предусмотреть методы для создания объектов, перемещения на плоскости, изменения размеров и вращения на заданный угол. Описать свойства для получения состояния объекта. При невозможности построения треугольника выбрасывается исключение.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 4

Построить описание класса, содержащего информацию о почтовом адресе организации. Предусмотреть возможность раздельного изменения составных частей адреса и проверки допустимости вводимых значений. В случае недопустимых значений полей выбрасываются исключения.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 5

Составить описание класса для представления комплексных чисел. Обеспечить выполнение операций сложения, вычитания и умножения комплексных чисел.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 6

Составить описание класса для вектора, заданного координатами его концов в трехмерном пространстве. Обеспечить операции сложения и вычитания векторов с получением нового вектора (суммы или разности), вычисления скалярного произведения двух векторов, длины вектора, косинуса угла между векторами.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 7

Составить описание класса прямоугольников со сторонами, параллельными осям координат. Предусмотреть возможность перемещения прямоугольников на плоскости, изменение размеров, построение наименьшего прямоугольника, содержащего два заданных прямоугольника, и прямоугольника, являющегося общей частью (пересечением) двух прямоугольников.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 8

Составить описание класса для представления даты. Предусмотреть возможности установки даты и изменения ее отдельных полей (год, месяц, день) с проверкой допустимости вводимых значений. В случае недопустимых значений полей выбрасываются исключения. Создать методы изменения даты на заданное количество дней, месяцев и лет.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 9

Описать класс ≪файл≫, содержащий сведения об имени, дате создания и длине файла. Предусмотреть инициализацию с проверкой допустимости значений полей. В случае недопустимых значений полей выбрасываются исключения. Описать метод добавления информации в конец файла и свойства для получения состояния файла.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 10

Составить описание класса многочлена вида ах 2 + bх + с. Предусмотреть методы, реализующие:

• вычисление значения многочлена для заданного аргумента;

• операцию сложения, вычитания и умножения многочленов с получением нового объекта-многочлена;

• вывод на экран описания многочлена.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 11

Описать класс, представляющий треугольник. Предусмотреть методы для создания объектов, вычисления площади, периметра и точки пересечения медиан. Описать свойства для получения состояния объекта. При невозможности построения треугольника выбрасывается исключение.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 12

Описать класс, представляющий круг. Предусмотреть методы для создания объектов, вычисления площади круга, длины окружности и проверки попадания заданной точки внутрь круга. Описать свойства для получения состояния объекта.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 13

Описать класс для работы со строкой, позволяющей хранить только двоичное число и выполнять с ним арифметические операции. Предусмотреть инициализацию с проверкой допустимости значений. В случае недопустимых значений выбрасываются исключения.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 14

Описать класс дробей – рациональных чисел, являющихся отношением двух целых чисел. Предусмотреть методы сложения, вычитания, умножения и деления дробей.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 15

Составить описание класса для представления времени. Предусмотреть возможности установки времени и изменения его отдельных полей (час, минута, секунда) с проверкой допустимости вводимых значений. В случае недопустимых значений полей выбрасываются исключения. Создать методы изменения времени на заданное количество часов, минут и секунд.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 16

Описать класс ≪комната≫, содержащий сведения о метраже, высоте потолков и количестве окон. Предусмотреть инициализацию с проверкой допустимости значений полей. В случае недопустимых значений полей выбрасываются исключения. Описать методы вычисления площади и объема комнаты и свойства для получения состояния объекта.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 17

Описать класс, представляющий нелинейное уравнение вида ах — cos(x) = 0. Описать метод, вычисляющий решение этого уравнения на заданном интервале методом деления пополам (см. Пр.р. 3 ≪Цикл с параметром for≫) и выбрасывающий исключение в случае отсутствия корня. Описать свойства для получения состояния объекта.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 18

Описать класс, представляющий квадратное уравнение вида ах 2 + bх + с. Описать метод, вычисляющий решение этого уравнения и выбрасывающий исключение в случае отсутствия корней. Описать свойства для получения состояния объекта.

Написать программу, демонстрирующую все разработанные элементы класса.

Вариант 19

Описать класс ≪процессор≫, содержащий сведения о марке, тактовой частоте, объеме кэша и стоимости. Предусмотреть инициализацию с проверкой допустимости значений полей. В случае недопустимых значений полей выбрасываются исключения. Описать свойства для получения состояния объекта.

Описать класс ≪материнская плата≫, включающий класс ≪процессор≫ и объем установленной оперативной памяти. Предусмотреть инициализацию с проверкой допустимости значений поля объема памяти. В случае недопустимых значений поля выбрасывается исключение. Описать свойства для получения состояния объекта.

Написать программу, демонстрирующую все разработанные элементы классов.

Вариант 20

Описать класс ≪цветная точка≫. Для точки задаются координаты и цвет. Цвет описывается с помощью трех составляющих (красный, зеленый, синий). Предусмотреть различные методы инициализации объекта с проверкой допустимости значений. Допустимым диапазоном для каждой составляющей является [0, 255].

В случае недопустимых значений полей выбрасываются исключения. Описать свойства для получения состояния объекта и метод изменения цвета.

Написать программу, демонстрирующую все разработанные элементы класса.

Видео:Нелинейные уравнения. Практическая часть. 9 класс.Скачать

Лабораторные работы на тему «программа на си шарп нелинейные уравнения»

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Отзывы на автора Анна

Все выполнено отлично, но есть небольшие недочеты. Спасибо!

Качественно и быстро выполнено задание! Спасибо.

Отлично сделанная работа. Спасибо!

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Напишем.ру — биржа помощи студентам!

95 000 экспертов

На твой заказ откликнуться несколько исполнителей, и ты сам сможешь выбрать с кем работать.

Система аукциона надежно защищает от переплат. Эксперт оценивает задание, а ты выбираешь стоимость.

Предоплата от 25%

Можно не вносить всю сумму сразу. Заказ пойдет в работу сразу после предоплаты.

Наши эксперты работаю с любыми системами проверки уникальности. Просто укажите в задании какая система нужна.

Эксперт не получает оплату пока не вышлет готовое задание. Даём гарантий период на каждый заказ, заключаем договор. Всегда на связи и всегда готовы помочь.

Псс. где-то на этой странице спрятан код на скидку .

• от 2 дней
• в среднем 1970 р.
• уникальность 70%

Код скидки на 10% secret10 введите перед оплатой

• от 1 дня
• в среднем 500 р.
• уникальность 50%

Код скидки на 5% secret5 введите перед оплатой

• от 1 дня
• в среднем 535 р.
• уникальность 50%

Код скидки на 7% secret7 введите перед оплатой

• от 5 дней
• в среднем 7000 р.
• уникальность 70%

Код скидки на 11% secret11 введите перед оплатой

• от 1 дня
• в среднем 700 р.
• уникальность 90%

Код скидки на 7% secret7 введите перед оплатой

Отчет по практике

• от 1 дня
• в среднем 700 р.
• уникальность 70%

Код скидки на 11% secret11 введите перед оплатой

• от 1 дня
• в среднем 700 р.
• уникальность до 100%

Код скидки на 10% secret10 введите перед оплатой

Код скидки на 5% secret5 введите перед оплатой

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Остались вопросы?

Здесь вы найдете ответы

Какова стоимость написания работы?

Стоимость выполнения заказа напрямую зависит от таких факторов, как отрасль науки, тема, срочность, наличие исходных материалов и готовых глав. На размер цены влияет также опыт исполнителя. Новички обычно указывают в заявке более низкую сумму, чем имеющие опыт авторы.

За какой период выполняется заказ?

Средний срок написания работы составляет 3 суток с момента подачи заявки. Если речь идет о сложных темах, требующих проработки огромного количества материала, то период увеличивается. Узнать о возможных сроках можно, ознакомившись с откликами авторов, которые они присылают после публикации заказа.

Нужно ли вносить аванс при подаче заказа?

Да, такая необходимость существует. Объем предоплаты напрямую зависит от желания исполнителя. В отклике он может указать 25, 50 или 100% от общей стоимости. Средства являются своеобразной гарантией выполнения сторонами условий соглашения. Деньги не сразу попадают на счет автора, а блокируются на счету биржи. Автор может воспользоваться средствами только после полного завершения заказа.

Как оплачивают заказы?

Биржа предоставляет клиентам возможность оплатить услуги разными способами. Это может быть Qiwi, Яндекс.Деньги, банковские карты, Халва и другие варианты. Детальную информацию можно получить в личном кабинете или у менеджеров компании.

Есть ли возможность вернуть материалы на доработку, и нужно ли за это платить?

Вернуть заказ на доработку можно в период согласования его с клиентом. Этот срок варьируется от 10 до 30 дней и напрямую зависит от типа работы.

Какие существуют гарантии для клиентов?

Интересы клиента защищены договором оферты. С его содержанием можно ознакомиться на сайте.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

6. Нелинейные уравнения и системы в SCILAB

1 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB Нелинейные уравнения и системы в SCILAB Если нелинейное уравнение достаточно сложное, то отыскание его корней процесс нетривиальный. Рассмотрим, какими средствами обладает Scilab для решения этой задачи Решение нелинейных уравнений В общем случае аналитическое решение уравнения f(x)=0 можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами. Численное решение уравнения проводят в два этапа: отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень, эти промежутки называют интервалами изоляции корня, определить их можно, изобразив график функции или любым другим методом основанным на том, что непрерывная функции f(x) имеет на интервале [a,b] хотя бы один корень, если она поменяла знак f(a) f(b) 2 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 2 полинома f с коэффициентом 3. —>p=poly(3,’x’,’r’); —>f=poly(3,’x’,’c’); —>p p = x —>f f = 3 Листинг 6.1. На листинге 6.2 приведены примеры создания более сложных полиномов. —>poly([1 0 2],’x’) 2 3 2x — 3x + x —>poly([1 0 2],’x’,’c’) x —>poly([-2 2],’x’) x Листинг 6.2 Листинг 6.3 содержит примеры операций с полиномами. —>p1=poly(2,’x’,’c’) p1 = 1-2x —>p2=poly(3,’x’,’c’) p2 = 3-2x —>p1/p2 1-2x x —>p1*p x + 4x Листинг 6.3 Решим несколько алгебраических уравнений. ЗАДАЧА 6.1. Найти корни полинома 2x 4 8x 3 +8x 2 1=0. Для решения этой задачи необходимо задать полином р. Сделаем это при помощи функции poly, предварительно определив вектор коэффициентов V. Обратите внимание, что в уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю. Отыскание корней полинома при помощи функции roots(p) приведено в листинге 6.4. Графическое решение, показанное на рис. 6.1 позволяет убедится,

3 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 3 что корни найдены верно. —>V=[ ]; —>p=poly(v,’x’,’c’) p = x — 8x + 2x —>X=roots(p) X =! !! !! !! ! Листинг 6.4 Рис График функции y=2x 4 8x 3 +8x 2 1 ЗАДАЧА 6.2. Найти корни полинома x x x 1=0. Решение этой задачи аналогично решению предыдущей. Разница заключается в способе вызова необходимых для этого функций. Не трудно заметить (листинг 6.5), что полином имеет один действительный и два комплексных корня, в отличии от полинома из задачи 6.1, в котором все корни действительные. Рис. 6.2 подтверждает это. —>roots(poly([ ],’x’,’c’))! !! i!! i! Листинг 6.5 ЗАДАЧА 6.3. Найти решение уравнения y(x)=0, если y(x)=x 4 18x Листинг 6.6 демонстрирует решение этой задачи. Обратите внимание на способ определения полинома.

4 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 4 Рис. 6.2.График функции y= x x x 1 —>x=poly(0,’x’); —>y=x^4-18*x^2+.6; —>roots(y)! !! !! !! ! Листинг 6.6 В Scilab существует функция fsolve(x0,f), которую так же можно применить для решения алгебраических уравнений. Подробно эта функция будет описана далее, так как ее можно использовать для решения нелинейных уравнений, отличных от алгебраических, и для решения систем линейных и нелинейных уравнений. ЗАДАЧА 6.4. Найти решение уравнения y(x)=0, если y(x)=x 5 x Решим эту задачу при помощи функции fsolve(x0,f), где x0 начальное приближение, f функция, описывающая левую часть уравнения y(x)=0. Листинг 6.7 содержит ход решения задачи. В первой строке происходит определение функции y(x) в виде исходного полинома. Во второй, вызывается команда fsolve(-2,y), для отыскания корней функции y. В качестве начального приближения задано число 2, так как не трудно определить (рис. 6.3), что полином имеет единственный действительный корень, в интервале от 2 до 1. —>deff(‘[f]=y(x)’,’f=x^5-x^3+1′) —>X=fsolve(-2,y) X = Листинг 6.7

5 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 5 Рис. 6.3.График функции y(x)=x 5 x 3 +1= x x x 1 Заметим, что заданное уравнение, кроме действительно корня, имеет и мнимые. Для отыскания всех корней полинома используйте функцию roots (листинг 6.8). —>roots(poly([ ],’x’,’c’))! i!! i!! i!! i!! ! Листинг 6.8 Далее будет рассмотрено применение функции fsolve для решения неалгебраических уравнений Трансцендентные уравнения Уравнение, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением. К трансцендентным уравнениям принадлежат показательные, логарифмические, тригонометрические. Рассмотрим применение функции fsolve для решения трансцендентных уравнений. ЗАДАЧА 6.5. Найти решение уравнения: ( x 1) x = 0. Выражение, стоящее в правой части уравнения можно представить в виде разности двух функций f(x) g(x)=0, где f ( x) = ( x 1), g ( x) = x. Тогда решение задачи будет выглядеть, так как показано в листинге 6.9. В качестве приближенного корня был выбран ноль, т.к. на рис. 6.4 видно, абсцисса точки пересечения линий f(x) и g(x) лежит в интервале [0;1].

6 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 6 —>deff(‘[y]=f1(x)’,’y1=((x-1)^2)^(1/3),y2=(x^2)^(1/3),y=y1-y2′) —>fsolve(0,f1) 0.5 Листинг 6.9 Рис График функций f ( x) = ( x 1) и g ( x) = x Рис ЗАДАЧА 6.6. Найти корни уравнения f(x)=e x /5 2(x-1) 2. Рис. 6.5: График функции f(x)=e x /5 2(x-1) 2 На рис видно, что график функции f(x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня. Последовательно вызывая функцию fsolve с различными начальными приближениями, так как показано в листинге 6.10, получим все решения заданного уравнения. —>deff(‘[y]=f(x)’,’y=exp(x)/5-2*(x-1)^2′) —>x(1)=fsolve(0,f); —>x(2)=fsolve(2,f); —>x(3)=fsolve(5,f);

7 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 7 —>x x =! !! !! ! Листинг 6.10 Кроме того, начальные приближения можно задать в виде вектора и тогда функцию можно вызвать один раз (листинг 6.11). —>fsolve([0;2;5],f)! !! !! ! Листинг 6.11 ЗАДАЧА 6.7. Вычислить корни уравнения sin(x) 0.4x=0 в диапазоне [ 5π;5π]. Решение задачи приведено в листинге >deff(‘[y]=fff(x)’,’y=-0.4+sin(x)’) —>V=[-5*%pi:%pi:5*%pi]; —>X=fsolve(V,fff); —>X X =! ! Листинг Системы уравнений Если заданы m уравнений с n неизвестными и требуется найти последовательность из n чисел, которые одновременно удовлетворяют каждому из m уравнений, то говорят о системе уравнений. Для решения систем уравнений в Scilab так же применяют функцию fsolve(x0,f). ЗАДАЧА 6.8. Решить систему уравнений: . Графическое решение системы (рис. 6.6) показывает, что она имеет две пары корней. Окружность и гипербола пересекаются в точках [0.8;0.6] и [-0.8;-0.6]. Эти значения приблизительны. Для того чтобы уточнить их, применим функцию fsolve, предварительно определив систему с помощью файл функции (листинг 6.13). function [y]=fun(x) y(1)=x(1)^2+x(2)^2-1; y(2)=x(1)^3-x(2); endfunction —>exec(‘c:program Filesscilab-4.0-rc1binfun.sce’); disp(‘exec done’); exec done —>fsolve([ ],fun)

8 Алексеев Е.Р., Чеснокова О.В. Нелинейные уравнения и системы в SCILAB. 8 —>fsolve([ ],fun) Листинг 6.13 Рис Графики функции x 2 +y 2 =1 и x 3 y=0. ЗАДАЧА 6.9. В данной задаче исследуется система из трех нелинейных уравнений с тремя неизвестными (листинг 6.13). function [y]=fun(x) y(1)=x(1)^2+x(2)^2+x(3)^2-1 y(2)=2*x(1)^2+x(2)^2-4*x(3) y(3)=3*x(1)^2-4*x(2)+x(3)^2 endfunction —>exec(‘d:scilab 3fun’);disp(‘exec done’);//вызов функции exec done —>fsolve([ ],fun)//решение системы! ! Листинг 6.14

Видео:Нелинейные уравнения. Практическая часть. 9 класс.Скачать

Моделирование динамических систем: решение нелинейных уравнений

Конечной целью математического моделирования в любой области знаний является получение количественных характеристик исследуемого объекта. Некоторые параметры пушки, стрельбу из которой мы моделировали в прошлый раз, были заданы в условии задачи: начальная скорость снаряда, его калибр и материал, из которого он изготовлен. Угол наклона ствола можно отнести к варьируемым параметрам: любое серьезное орудие допускает наводку, в том числе и в вертикальной плоскости.

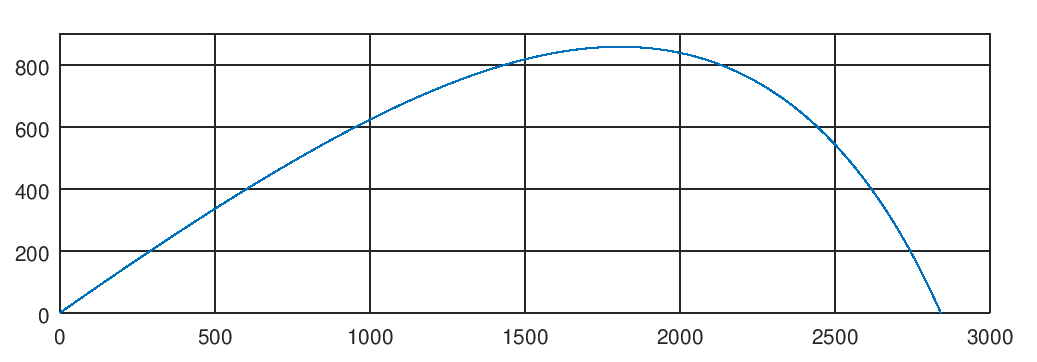
На выходе мы получили траекторию полета снаряда, что дает нам ориентировочные представления о характеристиках орудия: при заданных параметрах мы получили дальность стрельбы чуть более 2,5 км и высоту подъема снаряда чуть выше 800 метров. Точнее мы сказать не можем, вернее можем, если с карандашиком по сетке определим координаты нужных точек на графике. Но это, как известно, не наш метод. Хорошо бы получить эти данные с точностью, обеспечиваемой используемыми нами инструментами и без ручного труда. Вот об этом мы сегодня и поговорим.

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

1. Постановка задачи

Итак, построенная в прошлый раз математическая модель позволяет нам, для любого момента времени, определить координаты и скорость снаряда. По сути мы получили функции, которые позволяют вычислить следующие параметры траектории:

как функции времени. Высота полета снаряда это y(t). Если мы определим в какой момент времени высота становится равна нулю, то есть решим уравнение

относительно времени, то мы найдем момент времени в который снаряд упал на землю. Координата и будет дальность полета снаряда.

Как найти максимальную высоту подъема снаряда? Из графика траектории видно, что по мере подъема снаряда его траектория становится всё более и более пологой, пока в экстремальной точке скорость на мгновение становится горизонтальной и дальше снаряд движется вниз.

Говоря языком математики, необходимо найти точку экстремума функции . А что надо для этого сделать? Приравнять к нулю её производную! В данном случае производную по времени, то есть решить уравнение

ведь производная от вертикальной координаты по времени есть вертикальная проекция скорости. Корень этого уравнения, есть момент времени, когда снаряд достигнет максимальной высоты. Соответственно, интересующая нас высота

Просто? Более чем.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

2. Уравнение, которого нет

И вот тут котенка Гава, как известно, ждут неприятности. Начнем с того, что даже если уравнение задано в виде формулы (аналитически) не всегда удается найти его решение. Вот например

Как вам? Простенько, но попробуйте найти икс, используя всё то, чему вас учили в школе. То-то же…

Введем замену , тогда
begin
&u , e^ = 1 \
&u , e^ = e^ \
&-u , e^ = -e^
end
Пусть теперь , тогда

Теперь делаем финт ушами. Математики прошлого хорошо поработали за нас. Если задана функция вида

то обратная ей функция, называется W-функцией Ламберта.

Не в даваясь в теорию ФКП, в которой я мало смыслю, скажу, что число попадает в интервал в котором функция Ламберта многозначна, значит корня будет два

откуда, раскручивая назад все замены получаем ответ

Приближенно этот ужас равен

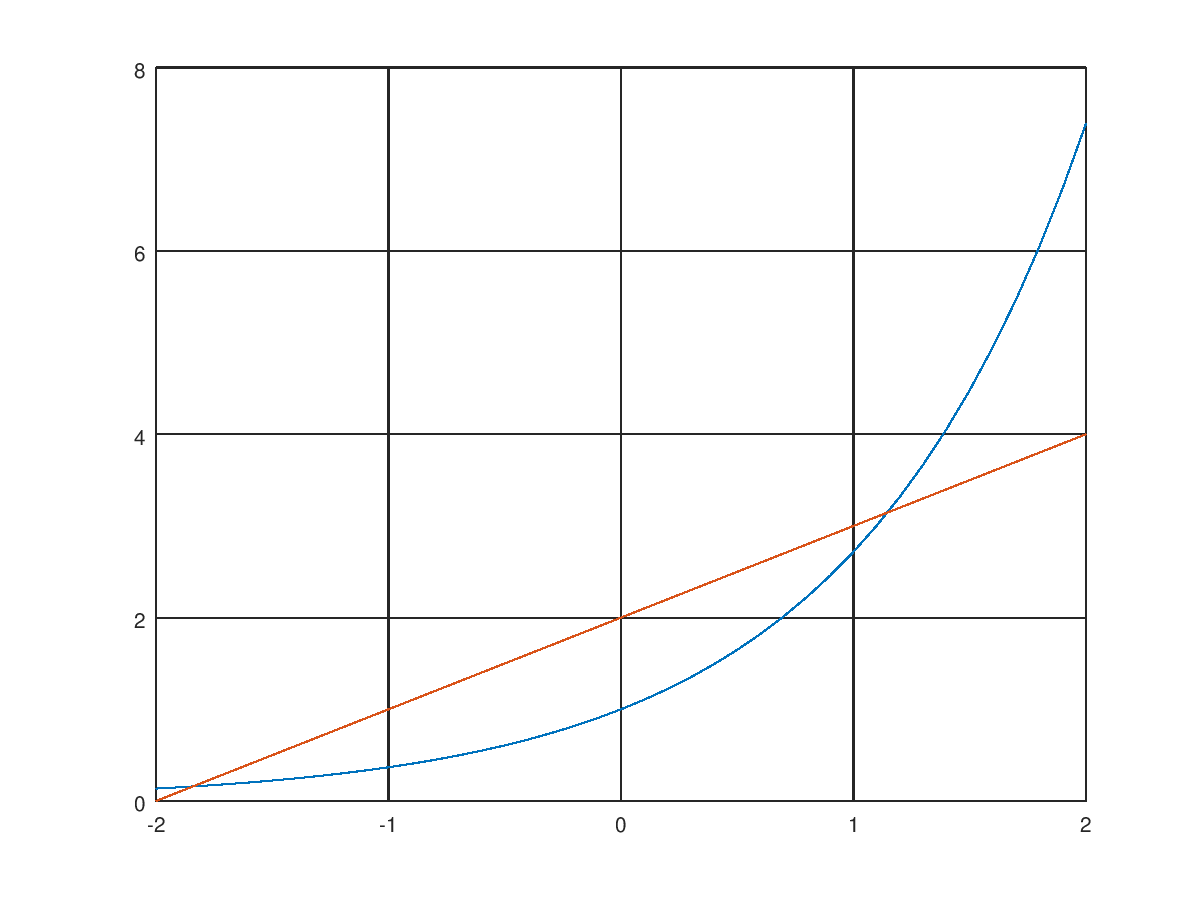
Решение такого уравнения придется искать численно, тем более что очевидно его графическое решение

В случае с моделью пушки всё несколько коварнее — наше уравнение задано даже не формулой. Оно задано, грубо говоря, таблицей значений фазовых координат, полученных для вполне конкретных параметров выстрела. У нас нет уравнения!

Ну так нам никто не мешает, чёрт возьми, это уравнение построить. Но, прежде чем начать писать скрипты, хочу извинится перед читателем, что ввёл его в заблуждение. В одном файле скрипта Octave можно размещать несколько функций, и имя файле на обязательно должно совпадать с именем функции. Достаточно, чтобы скрипт не начинался с определения функции.

Создадим новый скрипт в том же каталоге, где расположены файлы ballistics.m, f.m и f_air.m. Назовем его, например cannon.m. Для начала зададимся параметрами снаряда, начальной скоростью и направлением выстрела

А теперь напишем функцию, которая будет вычислять значения фазовых координат для произвольного момента времени

Обратите внимание, теперь в качестве моментов времени, передаваемых функции решения уравнения мы берем всего два значения: начальный момент времени (t = 0) и интересующий нас момент времени. Соответственно, переменная solv будет содержать два вектора фазовых координат: начальный и тот который нам нужен. Собираем все компоненты конечной точки фазовой траектории в вектор Y и возвращаем его значение из функции.

Теперь нам ничего не стоит определить зависимость высоты полета снаряда от времени

протестируем полученную функцию

При запуске скрипта на исполнение мы увидим в командном окне следующий вывод

Отлично, функция работает! Аналогично определим и функцию вычисления горизонтальной дальности

Видно, что для вычисления высоты и дальности мы каждый раз интегрируем уравнения движения, от начального до интересующего нас момента времени. Таким образом мы получили зависимость, не выражаемую конкретной формулой. Это довольно круто.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

3. Принципы численного решения нелинейных уравнений

Методы численного решения нелинейных и трансцендентных уравнений заточены под решение уравнений вида

К такой форме легко привести любое уравнение. Например

где . Корни этого, эквивалентного уравнения, равны корням исходного. Если мы построим график функции f(x), то увидим такую картинку

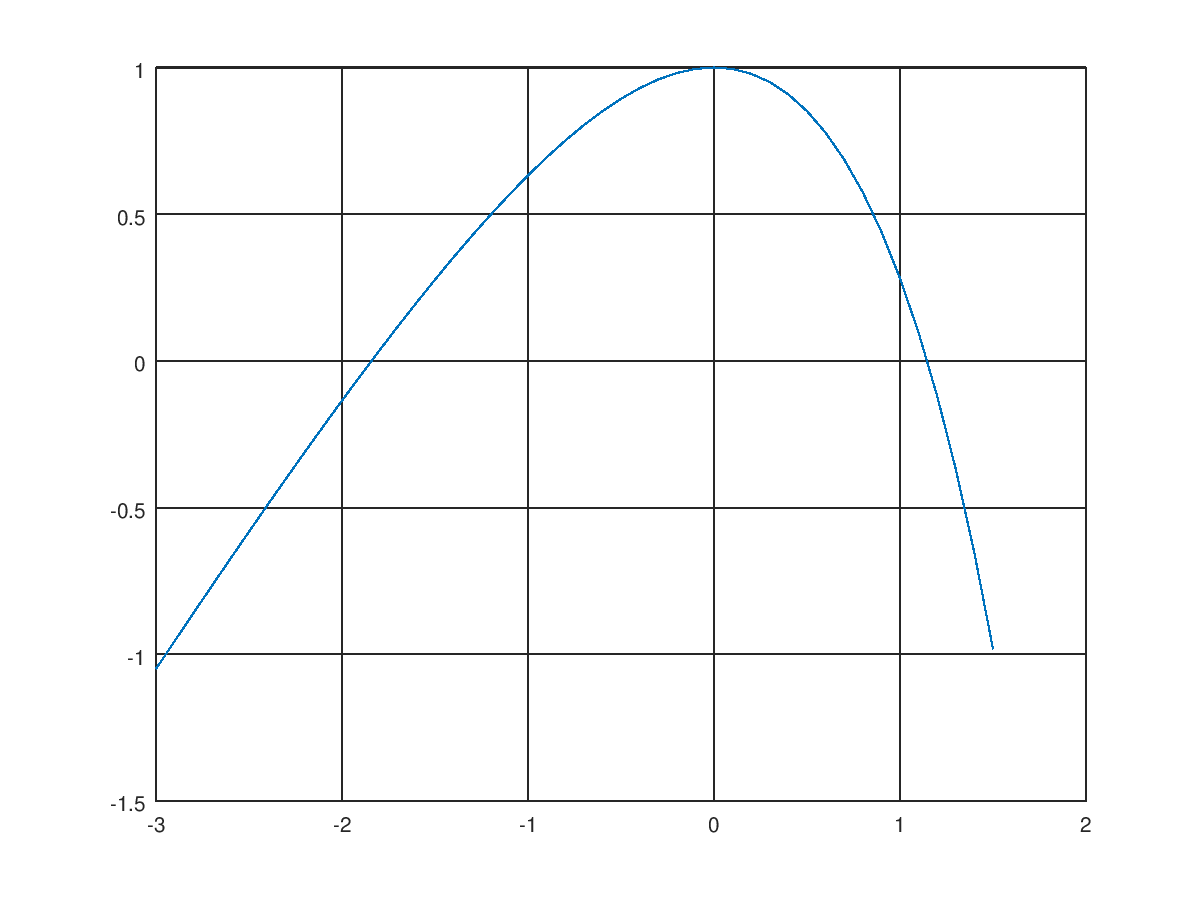
корни уравнения это значения аргумента в тех точках, где график пересекает ось x.

Все методы численного решения таких уравнений включают в себя два этапа:

1. Поиск начального приближения корня
2. Уточнение корня с заданной погрешностью

Под начальным приближением понимают значение аргумента f(x), максимально близкое к корню, либо достаточно близкое, чтобы обеспечить сходимость метода за разумное количество итераций.

Простейшим методом является метод простых итераций. Для применения этого метода уравнение преобразуют к виду

и выполняю расчеты по рекуррентной формуле

В нашем примере

Посмотрим на график. У уравнения два корня. Найдем крайний левый корень, выбрав в качестве начального приближения

Ага, видно, что начиная с шестой итерации четвертый знак получающегося числа остается неизменным. Значит мы нашли корень уравнения с погрешностью менее 10 -4 на шестой итерации.

Все бы хорошо, но метод простых итераций не всегда сходится. Попробуйте найти второй корень этого уравнения, задавшись любым, сколь угодно близким начальным приближением — у вас ничего не выйдет: каждое новое значение будет уходить от корня всё дальше и дальше. Сходимости метода можно добиться, существуют способы, но на практике это существенно осложняет нам жизнь. Поэтому для нахождения второго корня применим другой метод. Разложим исследуемую функцию в ряд Тейлора, в окрестности начального приближения

Ограничимся членами первого порядка малости, заменив саму функцию f(x) касательной к её графику в точке x₀

и приравняв полученное выражение к нулю, решим его относительно x

Получаем итерационную формулу

В нашем примере

В качестве начального приближения берем и пытаемся выполнять итерации

Как видно, этот метод сошелся за четыре итерации с точностью до четырех знаков. Этот метод называют методом Ньютона. Его достоинством является быстрая сходимость. Среди недостатков: высокая чувствительность к точности начального приближения и необходимость вычислять производную левой части уравнения. В случае, когда для уравнения нет аналитического выражения, приходится прибегать к мерзкой операции численного дифференцирования, что не всегда удобно и возможно.

Эти примеры я привел, чтобы объяснить общий принцип. Кроме этих двух методов существует ещё масса методов, например:

• Метод бисекции — отличается гарантированной сходимостью, однако с довольно низкой скоростью
• Метод хорд — не требует вычисления производной функции, обладает неплохой скоростью сходимости

Все перечисленные методы требуют предварительной подготовки, в виде поиска начального приближения или интервала изоляции корня — интервала изменения аргумента f(x), на границах которого функция меняет знак. В этом случае можно с уверенность сказать (при условии непрерывности функции!) что внутри интервала изоляции есть хотя бы один корень.

Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

4. Определяем параметры траектории пушечного ядра

Итак, найдем момент времени, когда снаряд упадет на землю. Прежде всего, определим интервал изоляции корня

Делаем это исходя из физического смысла задачи — после сразу выстрела высота полета снаряда неотрицательна. Перебираем все моменты времени, начиная от нуля, до тех пор, пока высота не станет отрицательна. Перебираем с достаточно крупным шагом (1 секунда) чтобы процедура не была слишком длительной, ведь на каждом шаге мы заново интегрируем дифференциальные уравнения движения, что весьма накладно сточки зрения вычислительных затрат. Как только высота станет отрицательной, заканчиваем перебор. Корень уравнения h(t) = 0 находится где-то внутри интервала [a, b]. Начальное приближение берем в середине этого интервала

Теперь отдаем уравнение на съедение процедуре решения нелинейных уравнений Octave

Функция fsolve() на вход принимает функцию, описывающую левую часть уравнения f(x) = 0 и значение начального приближения. Возвращает значение корня, вычисленное с заданной точностью. С какой точностью? Пока не будем задаваться этим вопросом и воспользуемся настройками по-умолчанию, на данном этапе они нас устраивают.

Получив значение момента времени падения, вычисляем дистанцию от позиции стрельбы

Аналогичным образом находим момент времени когда обнуляется вертикальная проекция скорости и вычисляем высоту полета снаряда в этот момент

В командном окне можно увидеть результаты работы программы

а также посмотреть, с какой точностью были решены уравнения

Для наших учебных целей точность вполне приемлема.

🎥 Видео

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

СИСТЕМА УРАВНЕНИЙ нелинейных 9 класс алгебраСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать