Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.
Пусть (a; 0) — координаты точки касания окружности с осью Ox. Тогда (см. рисунок) точка касания окружности с осью Oy имеет координаты (0; a), центр окружности имеет координаты (a; a) и радиус окружности равен a, поскольку окружность проходит через точку A(2; 1), у которой каждая координата больше нуля. Это означает, что окружность расположена в I квадранте, в котором a > 0.
Следовательно, уравнение окружности имеет вид (x — a) 2 + (y — a) 2 = a 2 .
Так как окружность проходит через точку A(2; 1), то имеем (2 — a) 2 + (1 — a) 2 = a 2 , откуда a = 1 или a = 5.
Искомое уравнение окружности: (x — 1) 2 + (y — 1) 2 = 1 или (x — 5) 2 + (y — 5) 2 = 25.
Видео:Уравнение окружности (1)Скачать
Задача 28098 4.3.4) Найти уравнение окружности.
Условие
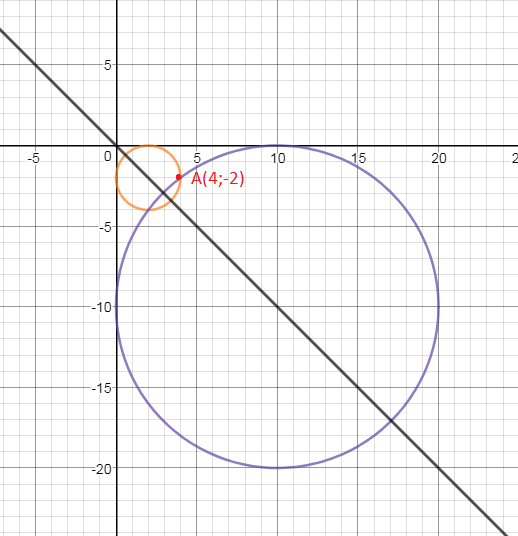
4.3.4) Найти уравнение окружности, касающейся осей координат и проходящей через точку (4; -2).
Решение
Окружность касается осей координат и проходит через точку, расположенную в четвертой координатной четверти, значит центр окружности лежит на биссектрисе второго и четвертого координатных углов, т.е на прямой y = — x.
и потому центр окружности имеет координаты (R;-R)
Следовательно, уравнение окружности имеет вид
(x — R)^2 + (y -(- R))^2 = R^2.
Поскольку точка A(4;-2) лежит на окружности, координаты этой точки удовлетворяют полученному уравнению,
т.е.
(4 — R)^2 + (-2 + R)^2 = R^2.
16-8R+R^2+4-4R+R^2=R^2
R^2-12R+20=0
D=144-80=64
R=2 или R=10
(x — 2)^2 + (y+2)^2 = 4 или
(x — 10)^2 + (y+10)^2 = 100
. 
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать
Практическая работа по теме: «Кривые второго порядка»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Практическая работа № 5 Тема: «Кривые второго порядка» Вариант 1
1. Составить уравнение окружности с центром в заданной точке S и данным радиусом r : S (4; -7), r =5;
2. Для указанных окружностей определить координаты центра S и радиус r : а) 
б) 
3. Составить уравнение окружности, касающейся осей координат и проходящей через точку М (2; 1).
4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов: 
5. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот гиперболы: а) 
б) 
6. Найти координаты фокуса и написать уравнение директрисы для параболы 
7. Составить уравнение параболы с вершиной в начале координат, зная координаты фокуса: F ( 0; 4).
Практическая работа № 5 Тема: «Кривые второго порядка» Вариант 2
1. Составить уравнение окружности с центром в заданной точке S и данным радиусом r : S (-6; 3), r = 
2. Для указанных окружностей определить координаты центра S и радиус r : а) 
б) 
3. Окружность, касающаяся осей координат, проходит через точку М (-2: -4). Написать её уравнение.
4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов: 
5. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот гиперболы: а) б) 
6. Найти координаты фокуса и написать уравнение директрисы для параболы 
7. Составить уравнение параболы с вершиной в начале координат, зная координаты фокуса: F (0; — 3).
Практическая работа № 5 Тема: «Кривые второго порядка» Вариант 3
1. Составить уравнение окружности с центром в заданной точке S и данным радиусом r : S (4; -7), r =5;
2. Для указанных окружностей определить координаты центра S и радиус r : а)
б)
3. Составить уравнение окружности касающейся координатных осей и лежащей в IV четверти, если ее радиус равен 
.
4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов: 
5. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот гиперболы: а) 
б) 
6. Найти координаты фокуса и написать уравнение директрисы для параболы 
7. Составить уравнение параболы с вершиной в начале координат, зная координаты фокуса: F (6; 0).
Практическая работа № 5 Тема: «Кривые второго порядка» Вариант 4
1. Составить уравнение окружности с центром в заданной точке S и данным радиусом r : S (-6; 3), r =
2. Для указанных окружностей определить координаты центра S и радиус r :
а) 
б) 
3. Составить уравнение окружности касающейся координатных осей и лежащей в IV четверти, если ее радиус равен 2.
4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов: 
5. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот гиперболы:
а) б)
6. Найти координаты фокуса и написать уравнение директрисы для параболы 
7. Составить уравнение параболы с вершиной в начале координат, зная координаты фокуса: F (-2,5; 0).
🎦 Видео
9 класс, 6 урок, Уравнение окружностиСкачать
ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать
Уравнение окружностиСкачать
начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать
Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать
№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать
Составляем уравнение окружностиСкачать
9 класс, 7 урок, Уравнение прямойСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Составляем уравнение прямой по точкамСкачать
УРАВНЕНИЕ ОКРУЖНОСТИСкачать
УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать
Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать
УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать
