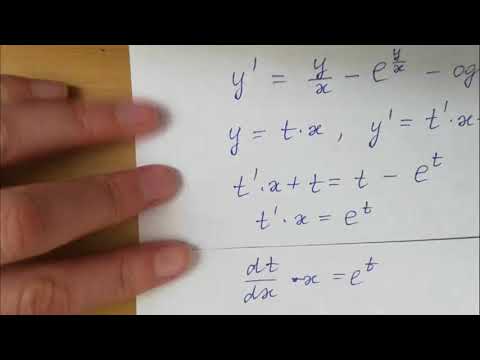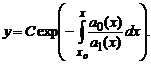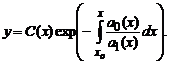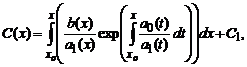Однородные дифференциальные уравнения 1 го порядка алгоритм решения методом произведения

Видео:Однородное дифференциальное уравнениеСкачать

Определение

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Как определить однородное дифференциальное уравнение

Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx : y → ty , x → tx . Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.

Пример

Определить, является ли данное уравнение однородным

Делаем замену y → ty , x → tx .

Делим на t 2 .

.
Уравнение не содержит t . Следовательно, это однородное уравнение.

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Метод решения однородного дифференциального уравнения

Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux . Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux ,
где u — функция от x . Дифференцируем по x :
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f ( u ) – u ) .

При f ( u ) – u ≠ 0 и x ≠ 0 получаем:

Интегрируем:

Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:

Заменим постоянную интегрирования C на ln C , тогда

Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C . Тогда общий интеграл примет вид:

Далее следует рассмотреть случай f ( u ) – u = 0 .
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).

Всякий раз, когда мы, в процессе преобразований, делим какое-либо уравнение на некоторую функцию, которую обозначим как g ( x, y ) , то дальнейшие преобразования справедливы при g ( x, y ) ≠ 0 . Поэтому следует отдельно рассматривать случай g ( x, y ) = 0 .

Видео:Линейные однородные дифференциальные уравнения 1-го порядка. Высшая математика.Скачать

Пример решения однородного дифференциального уравнения первого порядка

Проверим, является ли данное уравнение однородным. Делаем замену y → ty , x → tx . При этом y′ → y′ .
,
,
.
Сокращаем на t .

Постоянная t сократилась. Поэтому уравнение является однородным.

Делаем подстановку y = ux , где u – функция от x .
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0 , |x| = x . При x ≤ 0 , |x| = – x . Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0 , а нижний – к значениям x ≤ 0 .
,
Умножаем на ± dx и делим на .

При u 2 – 1 ≠ 0 имеем:

Интегрируем:

Интегралы табличные,
.

Применим формулу:
( a + b )( a – b ) = a 2 – b 2 .
Положим a = u , .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.

Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C .

Умножаем на x и подставляем ux = y .
,
.
Возводим в квадрат.
,
,
.

Теперь рассмотрим случай, u 2 – 1 = 0 .
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 19-07-2012 Изменено: 24-02-2015

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Однородные дифференциальные уравнения
и приводящиеся к ним

Видео:5. Однородные дифференциальные уравнения. Часть 2.Скачать

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Линейные уравнения первого порядка

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y’+y=b(x) .

• Решение онлайн
• Видеоинструкция

Теорема. Пусть a₁(x) , a₀(x) , b(x) непрерывны на отрезке [α,β], a₁≠0 для ∀x∈[α,β]. Тогда для любой точки (x₀, y₀), x₀∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x₀) = y₀ и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a₁(x)y’+a₀(x)y=0 .
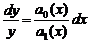
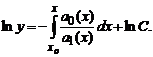
Разделяя переменные, получаем , или, интегрируя обе части, Последнее соотношение, с учетом обозначения exp(x) = e x , записывается в форме

Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде

Подставив это решение в исходное, после необходимых преобразований получаем 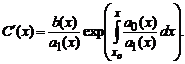Интегрируя последнее, имеем

где C₁— некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения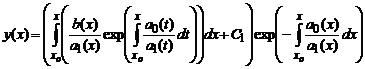
.

Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).

Пример . Решить уравнение y’ + 2y = 4x . Рассмотрим соответствующее однородное уравнение y’ + 2y = 0 . Решая его, получаем y = Ce -2 x . Ищем теперь решение исходного уравнения в виде y = C(x)e -2 x . Подставляя y и y’ = C'(x)e -2 x — 2C(x)e -2 x в исходное уравнение, имеем C'(x) = 4xe 2 x , откуда C(x) = 2xe 2 x — e 2 x + C₁ и y(x) = (2xe 2 x — e 2 x + C₁)e -2 x = 2x — 1 + C₁e -2 x — общее решение исходного уравнения. В этом решении y₁(x) = 2x-1 — движение объекта под действием силы b(x) = 4x, y₂(x) = C₁e -2 x -собственное движение объекта.

Пример №2 . Найти общее решение дифференциального уравнения первого порядка y’+3 y tan(3x)=2 cos(3x)/sin 2 2x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y’ = u’v + uv’.
3u v tg(3x)+u v’+u’ v = 2cos(3x)/sin 2 2x или u(3v tg(3x)+v’) + u’ v= 2cos(3x)/sin 2 2x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v’) = 0
2. u’v = 2cos(3x)/sin 2 2x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v’ = 0
Представим в виде: v’ = -3v tg(3x)

Интегирируя, получаем:

ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u’v = 2cos(3x)/sin 2 2x
u’ cos(3x) = 2cos(3x)/sin 2 2x
u’ = 2/sin 2 2x
Интегирируя, получаем:
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)

💡 Видео

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Однородные дифференциальные уравнения 1 порядкаСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Однородные дифференциальные уравнения: метод замены 1Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Однородные дифференциальные уравнения первого порядка #calculus #differentialequation #maths #Скачать

Однородные дифференциальные уравнения первого порядкаСкачать

Однородные дифференциальные уравненияСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Однородные дифференциальные уравнения первого порядкаСкачать