Рассмотрим однородные показательные уравнения второй и третьей степени (1-й — здесь).
Однородное уравнение — это уравнение, все члены которого имеют одинаковую суммарную степень.
Однородные уравнения второй степени в общем виде можно записать так:
где k1, k2, k3, a и b — некоторые числа, причём a и b — положительны и отличны от единицы.
Чтобы прийти к такому виду, почти всегда уравнение требуется предварительно преобразовать. Чаще всего уравнение записывают в виде
Запишем признаки, которые позволят отличить однородное уравнение от уравнений другого вида.
Признаки однородного показательного уравнения второй степени
- уравнение содержит ровно три степени с разными основаниями;
- показатели двух степеней ровно в два раза больше показателя третьей степени;
- основание этой третьей степени равно произведению оснований двух других степеней.
Однородные показательные уравнения второй степени решаются почленным делением обеих частей на наибольшую из степеней.
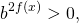
деление на степень не приводит к потере корней (то есть получаем уравнение, равносильное предыдущему).
ОДЗ: x∈R.Перепишем уравнение в виде
Разделим обе расти уравнения почтенно на 3 в степени 2x:
После упрощения приходим к уравнению
Это уравнение сводится к квадратному при помощи замены
где t>o. Оба корня квадратного уравнения
удовлетворяют условию t>0. Обратная замена
Сначала избавляемся от числовых слагаемых в показателях степеней, используя свойства степеней
представим степень с основанием 15 в виде произведения степеней с основаниями 3 и 5:
Делим обе части уравнения на 5 в степени 2x:
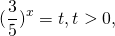
Оба корня положительны. Возвращаемся к исходной переменной:
По такому же принципу решаются однородные показательные уравнения 3-й степени.
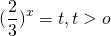
приводит к уравнению третьей степени
Представим -2=-1-1 и сгруппируем слагаемые
Общий множитель (t-1) вынесем за скобки
Получили уравнение типа «произведение равно нулю». приравниваем к нулю каждый множитель
Корень 1-го уравнения — t=1, второе уравнение не имеет корней. Обратная замена
- Системы с нелинейными уравнениями
- Нелинейные уравнения с двумя неизвестными
- Системы из двух уравнений, одно из которых линейное
- Однородные уравнения второй степени с двумя неизвестными
- Системы из двух уравнений, одно из которых однородное
- Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
- Примеры решения систем уравнений других видов
- Алгебра и начала анализа. Урок по теме «Однородные тригонометрические уравнения» (10-й класс)
- 🌟 Видео
Видео:Однородное показательное уравнение второй степени из ЕГЭСкачать

Системы с нелинейными уравнениями
 Нелинейные уравнения с двумя неизвестными Нелинейные уравнения с двумя неизвестными |
 Системы из двух уравнений, одно из которых линейное Системы из двух уравнений, одно из которых линейное |
 Однородные уравнения второй степени с двумя неизвестными Однородные уравнения второй степени с двумя неизвестными |
 Системы из двух уравнений, одно из которых однородное Системы из двух уравнений, одно из которых однородное |
 Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное |
 Примеры решения систем уравнений других видов Примеры решения систем уравнений других видов |
Видео:3B Однородные тригонометрические уравнения второй степени и уравнения, приводящиеся к нимСкачать

Нелинейные уравнения с двумя неизвестными
Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
| z = f (x , y) , | (1) |
причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .
Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
| f (x , y) = 0 , | (2) |
где f (x , y) – любая функция, отличная от функции
где a , b , c – заданные числа.
Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1 . Решить уравнение
| x 2 – 4xy + 6y 2 – – 12 y +18 = 0 . | (3) |
Решение . Преобразуем левую часть уравнения (3):
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y) 2 + 2(y – 3) 2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
решением которой служит пара чисел (6 ; 3) .
Пример 2 . Решить уравнение
| sin (xy) = 2 . | (5) |
вытекает, что уравнение (5) решений не имеет.
Ответ : Решений нет.
Пример 3 . Решить уравнение
| ln (x – y) = 0 . | (6) |
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
где y – любое число.
Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Системы из двух уравнений, одно из которых линейное
Определение 4 . Решением системы уравнений
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4 . Решить систему уравнений
 | (7) |
Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
Таким образом, решениями системы (7) являются две пары чисел

Ответ : (– 1 ; 9) , (9 ; – 1)
Видео:10й класс; Математика; Однородные тригонометрические уравнения I, II степениСкачать

Однородные уравнения второй степени с двумя неизвестными
Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
где a , b , c – заданные числа.
Пример 5 . Решить уравнение
| 3x 2 – 8xy + 5y 2 = 0 . | (8) |
Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
Ответ . Решениями уравнения (8) являются все пары чисел вида
( y ; y) или
где y – любое число.
Следствие . Левую часть уравнения (8) можно разложить на множители
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6 . Решить систему уравнений
 | (9) |
рассматривая его как квадратное уравнение относительно неизвестного x :

В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .

из второго уравнения системы (9) получаем уравнение
которое корней не имеет.
Ответ : (– 2 ; 2) , (2 ; – 2)
Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7 . Решить систему уравнений
 | (10) |
Решение . Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
 | (11) |
рассматривая его как квадратное уравнение относительно неизвестного x :

В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
которое корней не имеет.

из второго уравнения системы (11) получаем уравнение

корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ : (– 2 ; 3) , (2 ; – 3)
Видео:Однородное уравнение второй степениСкачать

Примеры решения систем уравнений других видов
Пример 8 . Решить систему уравнений (МФТИ)
Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
из которой находим
 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что 
Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9 . Решить систему из двух уравнений с тремя неизвестными
 | (17) |
Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Ответ : (4 ; 4 ; – 4)
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
Видео:Однородное уравнениеСкачать

Алгебра и начала анализа. Урок по теме «Однородные тригонометрические уравнения» (10-й класс)
Разделы: Математика
Класс: 10
- ввести понятие однородных тригонометрических уравнений I и II степени ;
- сформулировать и отработать алгоритм решения однородных тригонометрических уравнений I и II степени;
- научить учащихся решать однородные тригонометрических уравнений I и II степени;
- развивать умение выявлять закономерности, обобщать;
- стимулировать интерес к предмету, развивать чувство солидарности и здорового соперничества.
Тип урока: урок формирования новых знаний.
Форма проведения: работа в группах.
Оборудование: компьютер, мультимедийная установка
I. Организационный момент
Приветствие учащихся, мобилизация внимания.
На уроке рейтинговая система оценки знаний (учитель поясняет систему оценки знаний, заполнение оценочного листа независимым экспертом, выбранным учителем из числа учащихся). Урок сопровождается презентацией . Приложение 1.
II. Актуализация опорных знаний..
Домашняя работа проверяется и оценивается независимым экспертом и консультантами до урока и заполняется оценочный лист.
Учитель подводит итог выполнения домашнего задания.
Учитель: Мы продолжаем изучение темы “Тригонометрические уравнения”. Сегодня на уроке мы познакомимся с вами с еще одним видом тригонометрических уравнений и методами их решения и поэтому повторим изученное. Все виды тригонометрических уравнений при решении сводятся к решению простейших тригонометрических уравнений.
Проверяется индивидуальное домашнее задание, выполняемое в группах. Защита презентации “Решения простейших тригонометрических уравнений”
(Оценивается работа группы независимым экспертом)
III. Мотивация обучения.
Учитель: нам предстоит работа по разгадыванию кроссворда. Разгадав его, мы узнаем название нового вида уравнений, которые научимся решать сегодня на уроке.
Вопросы спроецированы на доску. Учащиеся отгадывают, независимый эксперт заносит в оценочный лист баллы отвечающим учащимся.
Разгадав кроссворд, ребята прочитают слово “однородные”.
IV. Усвоение новых знаний
Учитель: Тема урока “Однородные тригонометрические уравнения”.
Запишем тему урока в тетрадь. Однородные тригонометрические уравнения бывают первой и второй степени.
Запишем определение однородного уравнения первой степени. Я на примере показываю решение такого вида уравнения, вы составляете алгоритм решения однородного тригонометрического уравнения первой степени.
Уравнение вида аsinx + bcosx = 0 называют однородным тригонометрическим уравнение первой степени.
Рассмотрим решение уравнения, когда коэффициенты а и в отличны от 0.
Пример: sinx + 
Разделив обе части уравнения почленно на cosx, получим
Внимание! Делить на 0 можно лишь в том случае, если это выражение нигде не обращается в 0. Анализируем. Если косинус равен 0, то получается и синус будет равен 0, учитывая что коэффициенты отличны от 0, но мы знаем, что синус и косинус обращаются в нуль в различных точках. Поэтому эту операцию производить можно при решении такого вида уравнения.
Алгоритм решения однородного тригонометрического уравнения первой степени:
- Деление обеих частей уравнения на cosx, cosx
0
Уравнение вида аsin mx + bcos mx = 0 тоже называют однородным тригонометрическим уравнение первой степени и решат также деление обеих частей уравнения на косинус mх.
Уравнение вида a sin 2 x + b sinx cosx + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.
Пример: sin 2 x + 2sinx cosx – 3cos 2 x = 0
Коэффициент а отличен от 0 и поэтому как и предыдущем уравнении соsх не равен0 и поэтому можно воспользоваться способом деления обеих частей уравнения на соs 2 х.
Получим tg 2 x + 2tgx – 3 = 0
Решаем путем введения новой переменной пусть tgx = а , тогда получаем уравнение
Возвращаемся к замене
 |  |
Ответ:
Если коэффициент а = 0, то уравнение примет вид 2sinx cosx – 3cos 2 x = 0 решаем способом вынесения общего множителя cosx за скобки
Если коэффициент с = 0, то уравнение примет вид sin 2 x +2sinx cosx = 0
решаем способом вынесения общего множителя sinx за скобки .
Алгоритм решения однородного тригонометрического уравнения первой степени:
- Посмотреть, есть ли в уравнении член asin 2 x.
- Если член asin 2 x в уравнении содержится (т.е. а
0), то уравнение решается делением обеих частей уравнения на cos 2 x и последующим введение новой переменной.
- Если член asin 2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx.
Однородные уравнения вида a sin 2 m x + b sin mx cos mx + c cos 2 mx = 0 решаются таким же способом
Алгоритм решени однородных тригонометрических уравнений записан в учебнике на стр. 102.
V. Формирование навыков решения однородных тригонометрических уравнений
Открываем задачники стр. 53
1-я и 2-я группа решают № 361 в)
3-я и 4-я группа решают № 363 в)
Показывают решение на доске, объясняют, дополняют. Независимый эксперт оценивает.
Решение примеров из задачника
№ 361в)
sinx – 3cosx = 0
делим обе части уравнения на cosx 
№ 363в)
sin 2 x + sinxcosx – 2cos 2 x = 0
разделим обе части уравнения на cos 2 x, получим
tg 2 x + tgx – 2 = 0
решаем путем введения новой переменной
пусть tgx = а , тогда получаем уравнение
а 2 + а – 2 = 0
Д = 9
а1 = 1 а2 = –2
возвращаемся к замене
 |  |
VI. Самостоятельная работа
- 2 cosx –
2 = 0
- tg2x +1 = 0
- 2cos 2 x – 3cosx +1 = 0
- 3 sin 2 x + sinx cosx – 2 cos 2 x = 0
По окончанию самостоятельной работы меняются работами и взаимопроверка. Правильные ответы проецируются на доску.
Потом сдают независимому эксперту.
Решение самостоятельной работы
VII. Подведение итогов урока
- С каким видом тригонометрических уравнений мы познакомились на уроке?
- Алгоритм решения тригонометрических уравнений первой и второй степени.
VIII. Задание на дом
§ 20.3 читать. № 361(г), 363(б), повышенной трудности дополнительно
Если вписать верные слова, то получится название одного из видов тригонометрических уравнений.
- Значение переменной, обращающее уравнение в верное равенство? (Корень)
- Единица измерения углов? (Радиан)
- Числовой множитель в произведении? (Коэффициент)
- Раздел математики, изучающий тригонометрические функции? (Тригонометрия)
- Какая математическая модель необходима для введения тригонометрических функций? (Окружность)
- Какая из тригонометрических функций четная? (Косинус)
- Как называется верное равенство? (Тождество)
- Равенство с переменной? (Уравнение)
- Уравнения, имеющие одинаковые корни? (Равносильные)
- Множество корней уравнения? (Решение)
| № пп | Фамилия имя | Домашнее задание | Презентация | Познавательная активность уч-ся | Решение уравнений | Самостоятельная работа | Оценка |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 |
Рейтинговая система оценки знаний
- Домашнее задание – 12 баллов (на дом было задано 3 уравнения 4 х 3 = 12)
- Презентация – 1балл
- Активность уч-ся – 1ответ – 1 балл (4 балла максимально)
- Решение уравнений 1 балл
- Самостоятельная работа – 4 балла
“5” – 22 балла и более
“4” – 18 – 21 балл
“3” – 12 – 17 баллов
За высокую активность ставится дополнительная оценка.
🌟 Видео
Решение однородных показательных уравнений второй степениСкачать

Решение однородных тригонометрических уравнений 1-ой и 2-ой степениСкачать

Однородные уравнения 2Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Однородные тригонометрические уравнения II степени. Видеосправочник по математике #4Скачать

Решение однородных уравнений второй степениСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Однородные тригонометрические уравненияСкачать

Как решать однородные тригонометрические уравненияСкачать

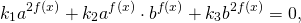
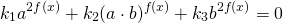
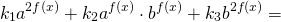
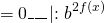
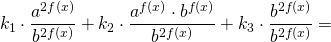
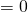
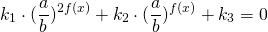
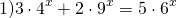
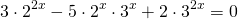
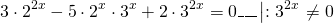
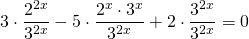
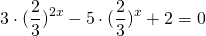
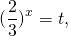
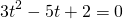
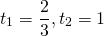
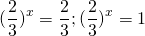
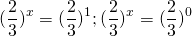
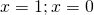
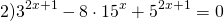
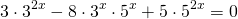
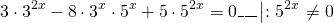
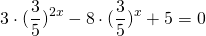
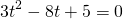
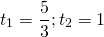
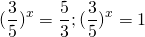
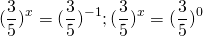
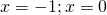
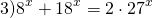
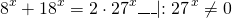
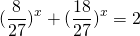
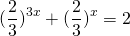
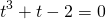
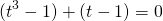
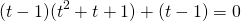
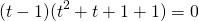
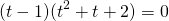
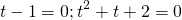
































 2 = 0
2 = 0
