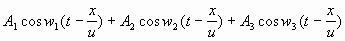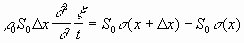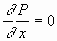§ 1. Понятие упругой волны. Поперечные и продольные волны. . 2
§ 2. Фронт волны. Длина волны. . 3
Глава II. Волновое уравнение.
§ 1. Математические сведения. . 4
§ 2. Упругие волны в стержне.
1) волновое уравнение. . 5
§ 3. Упругие волны в газах и жидкостях.
волновое уравнение; . 8
случай идеального газа . 9
Список использованной литературы. . 11
§1. Понятие волны. Поперечные и продольные волны.
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v . Процесс распространения колебаний в пространстве называется волной .
Частицы среды , в которой распространяется волна, не вовлекаются волной в поступательное движение , они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
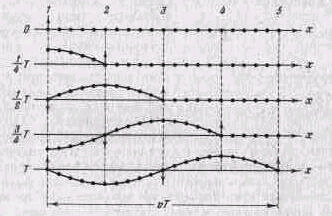
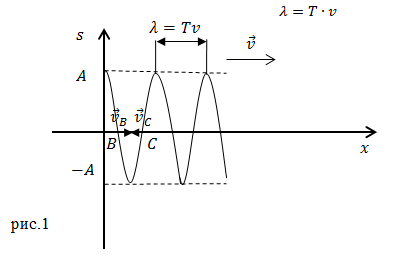
На рис. 1 показано движение частиц при распространении в среде поперечной волны. Номерами 1, 2 и т. д. обозначены частицы, отстоящие друг от друга на расстояние, равное 1/ 4vТ , т. е. на расстояние, проходимое волной за четверть периода колебаний,
совершаемых частицами. В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2 . По прошествии еще четверти периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигнет крайнего верхнего положения, а третья частица начнет смещаться вверх из положения равновесия. В момент времени, равный Т, первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. Волна к моменту времени T, пройдя путь vТ, достигнет частицы 5.
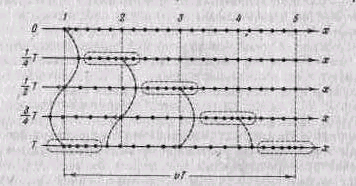
На рис. 2 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведения частиц в поперечной волне, могут быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево. Из рисунка видно, что при распространении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц (места сгущения частиц обведены на рисунке пунктиром), перемещающиеся в направлении распространения волны со скоростью v.
§2. Фронт волны. Длина волны.
На рис. 1 и 2 показаны колебания частиц, положения равновесия которых лежат на оси х. В действительности колеблются не только частицы, расположенные вдоль оси х, а совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны (или волновым фронтом ). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства,охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.
Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер.
Рассмотрим случай, когда плоская волна распространяется вдоль оси х. Тогда все точки среды, положения равновесия которых имеют одинаковую координату х (но различные значения координат y и z), колеблются в одинаковой фазе.
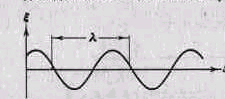
На рис. 3 изображена кривая, которая дает смещение 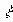
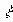
Расстояние 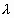
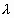
где v – скорость волны, Т – период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2П. Заменив в соотношении (1.1) Т через 1/ 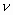
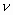
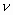
Рассмотрев кратко основные понятия, связанные с волной, перейдем к описательной стороне, т.е. волновому уравнению.
§1. Математические сведения.
Этот параграф является математическим введением к тому динамическому рассмотрению волн, которое будет дано в $2. Рассмотрим произвольную функцию
f(at-bx) (2.3) от аргумента аt—bх. Продифференцируем ее дважды по t :
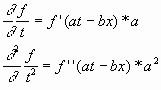
Здесь штрих означает дифференцирование по аргументу at—bx. Продифференцируем теперь нашу функцию дважды по х:
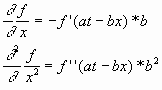
Сравнивая (2.4) и (2.5), мы убеждаемся, что функция (2.3) удовлетворяет уравнению
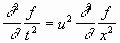
Легко видеть, что этому же уравнению удовлетворяет произвольная функция
f(at+bx) (2.7) (2.7) аргумента at+bx, а также сумма функций вида (2.3) и (2.7).
Функции (2.3) и (2.7) изображают при положительных a, b плоские волны, распространяющиеся, не деформируясь, со скоростью и в сторону соответственно возрастающих или убывающих значений х **).
Уравнение (2.6)—дифференциальное уравнение в частных производных, играющее в физике очень важную роль. Оно называется волновым уравнением. В математических курсах доказывается, что оно не имеет решений, отличных от тех, которые могут быть представлены функциями вида (2.3) и (2.7) или суперпозицией таких функций, например,
f 1 (at — bх) + f 2 (at+bx).
Всякий раз, когда из физических соображений можно установить, что та или иная физическая величина s удовлетворяет уравнению вида
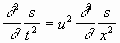
мы сможем на основании сообщенных здесь математических сведений заключить, что процесс изменений этой величины носит характер плоской, волны, распространяющейся в ту или другую сторону со скоростью и, или суперпозиции таких волн.
Вид функций f 1 , f 2 определяется характером движения источника волн, а такжеявлениями, происходящими на границе среды.
Пусть источником волнявляется плоскость х =0, причем на этой плоскости величина S колеблется но закону s =Acoswt. В этом случае от плоскости х= 0 распространяются вправо и влево волны
s= Acos(wt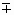
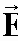
Из линейности волнового уравнения следует, что если ему удовлетворяют функции s 1 , s 2 ,s 3 , . в отдельности, то ему удовлетворяет также функция
S == S 1 + S 2 + S 3 + .
Рассмотрим несколько примеров.
а) Волновому уравнению удовлетворяют синусоидальные бегущиеволны
s 1 = Aсоs(wt — kx ), s 2 = Acos(wt+kx).
На основании принципа суперпозиции волновому уравнению удовлетворяет стоячая волна
являющаяся суперпозицией только что рассмотренных синусоидальных бегущих волн.
б) Волновому уравнению на основании принципа суперпозиции удовлетворяет всякая функция вида
S=
Это—функция вида f(at—bx); она изображает несинусоидальную волну, распространяющуюся без деформации всторону возрастающих х.
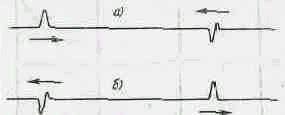
в) Пусть волны S 1 , S 2 , имеющие вид коротких импульсов, распространяются навстречу одна другой. В некоторый момент моментальный снимок суперпозиции S 1 + S 2 этих волн имеет вид, показанный на рис. 4,а. Через некоторое время моментальный снимок волны будет иметь вид, показанный на рис. 4, б, – волны пройдут “одна сквозь другую” и притом каждая так, как будто другой не существует.
§2. Упругие волны в стержне.
1. волновое уравнение.
В предыдущем параграфе мы рассмотрели математическую сторону волнового уравнения. В этом же параграфе я хотел бы на конкретном примере рассмотреть как работает тот математический аппарат.
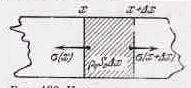
Применим второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+

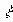
слева стоит произведение массы куска на ускорение д 2 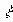
Разделим уравнение на S 0 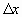
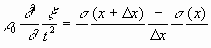
Перейдя к пределу при 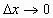
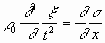
справедливое в каждой точке стержня. Оно указывает, что ускорение данной точки пропорционально частной производной напряжения по ж в этой точке.
Подставляя в (2.8) соотношение (2.7), получим:
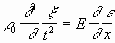
Вспомнив теперь формулу , содержащую определение деформации, и подставив ее в (2.9), получаем:
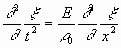
Это—волновое уравнение. Оно указывает, что смещение распространяется но стержню в виде волн
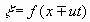
или образует суперпозицию таких волн. Скорость распространения этих волн (скорость звука в стержне)
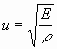
(мы опускаем для краткости индекс 0 у р). Эта скорость тем больше, чем жестче и чем легче материал. Формула (2.12)—одна из основных формул акустики.
Наряду со смещением 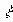
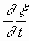
.движутся отдельные плоскости х = const (не смешивать с u ), деформация 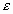
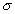
v=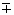
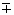
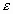
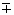
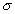
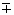
Таким образом, смещение, скорость, деформация и напряжение распространяются в виде связанных определенным образом между собой недеформирующихся волн, имеющих одну и ту же скорость и одинаковое направление распространения.
На рис.5 показан пример “моментальных снимков”, относящихся к одному и тому же моменту времени, смещения, деформации и скорости в одной и той же упругой волне. Там, где смещение имеет максимум или минимум, деформация и скорость равны нулю, так как они обе пропорциональны производной f» <x 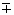
Сравнивая формулы (2.13а), (2.13в) и принимая во внимание (2.12) мы видим, что
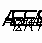
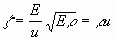
есть величина, не зависящая от вида функции f и целиком определяемая свойствами материала. Эта величина называется удельным акустическим сопротивлением материала. Она является, как мы видим, наряду с u его важнейшей акустической характеристикой. Название величины 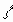
§ 2. Упругие волны в газах и жидкостях
Мы рассматриваем здесь газ или жидкость (так же как твердое тело в предыдущих параграфах) как сплошную непрерывную среду, отвлекаясь от его атомистической структуры. Под смещением 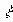
Будем считать, что рассматриваемый газ или жидкость находятся в очень длинной цилиндрической трубе, образующие которой параллельны оси х, и что смещение зависит только от одной координаты х. Мы можем применить к столбу газа или жидкости, заполняющему трубу, те же рассуждения, что и к стержню (§ 1). Мы придем, таким образом, к уравнению
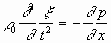
где р = — 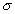
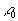
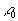
Уравнение (2.16) применимо и в случае плоских волн в неограниченной жидкой или газообразной среде (можно мысленно выделить цилиндрический столб, параллельный направлению распространения и применить к нему те же рассуждения, что к столбу, заключенному в трубе).
Как известно из термодинамики, р есть функция плотности данной массы газа (или жидкости) и ее температуры. Температура в свою очередь изменяется при сжатии и разрежении. Теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями. В термодинамике показывается, что в этом случае (если можно пренебречь внутренним трением и некоторыми другими явлениями температура является однозначной функцией плотности , и следовательно, давление также.
При заданной деформации 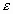
В газах и в жидкостях за некоторыми исключениями (например вода, при температуре ниже 4° С) температура растет при сжатии и уменьшается при расширении.
Есть однозначная функция плотности:
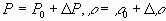
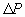
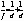
Подставляя первую формулу (2.18) в (2.16) и принимая во внимание, что при равновесии давление не зависит от х, т. е.
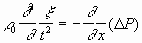
Найдем теперь связь между 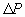
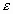
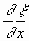
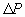
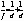
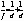
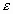
а) Подставляя (6.28) в (6.27), имеем:
P 0 +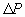
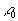
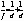
разлагая f( 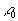
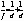
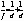
P 0 +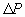
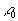
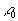
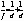
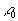
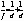
Так как P 0 = f( 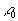
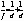
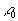
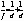
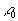
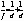
Здесь мы сделаем существенное предположение: будем считать уплотнения и разрежения настолько малыми, что допустимо пренебречь в разложении (2.20) членами, пропорциональными ( 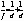
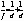
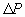
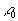
Тем самым мы ограничиваем себя исследованием волн малой интенсивности.
f’ (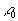
б) Объем V 0 в результате деформации превращается в объем
V=V 0 (1+ 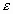
так как здесь поперечный размер (в отличие от твердого стержня) остается, постоянным, а длина превращается в . Но произведение плотности на объем, равное массе рассматриваемой порции вещества, не меняется:
Подставляя (2.18) и (2.21), получаем:
Пренебрегая и здесь высшими степенями малой величины , получаем:
Подставляя, наконец, (2.22) в (2.19), мы получаем волновое уравнение
Отсюда заключаем, что рассматриваемые малые деформации распространяются в виде плоских не деформирующихся волн; скорость распространения (скорость звука) тем больше, чем сильное в данной среде возрастает давление при адиабатическом возрастании плотности; она раина квадратному корню из производной давления по плотности, взятой при значении последней в отсутствие волны ( ).
2. Случай идеального газа . Идеальным газом называется газ, для которого справедливо уравнение состояния
где p – давление, V—объем одного моля, R— универсальная газовая постоянная, равная 8,3143 эрг/град, T—температура, измеренная по термодинамической шкале (“абсолютная температура”), или
где М— масса 1 моля, = M/V— плотность.
Воздух, кислород, азот, водород и многие другие газы при комнатной температуре и давлении порядка атмосферного можно рассматривать с достаточным для акустики приближением как идеальные газы.
Как учит термодинамика, в случае идеального газа соотношение (2.17) имеет вид
постоянная величина (С и С — теплоемкости газа соответственно при постоянном давлении и постоянном объеме). Следовательно, здесь
Еще задолго до Лапласа вопросом о скорости звука в воздухе занимался Ньютон. Он считал, что
т. е. не учитывал изменения температуры воздуха при распространении в нем звуковой волны, вследствие чего получил для скорости звука соотношение
Это соотношение можно получить из уравнения (2.24), подставляя в него (2.26а) вместо (2.26).
Для воздуха ( =1,4) при комнатной температуре (20° С, Т =293°) формула Ньютона дает u =290 м/сек, формула Лапласа и =340 м/сек. Сравнивая эти значения с теми, которые дает опыт (гл. V, § 3), мы видим, что формула Лапласа, в отличие от формулы Ньютона, хорошо согласуется с опытом. Формула Лапласа хорошо подтверждается на опыте и для других газов (но крайней мере при не очень высоких частотах.
Этим оправдывается предположение о том, что сжатие и разрежение газа в звуковой волне являются практически адиабатическими процессами.
Список использованной литературы.
- Горелик, Колебания и волны,
- И.В. Савельев, курс общей физики, т.2, М, 1988г.
- Б.М. Яворский, А.А. Пинский, Основы физики, т.2, М., 1972г.
Амплитуда вынужденных колебаний реактора при очень малой частоте 2 мм, а при резонансе 16 мм. Предполагая, что декремент затухания меньше единицы, определить его.
Две волны Х 1 =Аsin( wt-kl) и Х 2 =Аsin (wt+kl) с одинаковыми частотами 4Гц распространяются со v =960 см/сек. Они интерферируют между собой и образуют стоячую волну. Определить амплитуды точек стоячей волны через каждые 20 см, начиная отсчет от узла. Определить величину смещения и скорость этих точек для момента времени 7/24 сек.
Между приемником и стенкой расположен источник звуковых колебаний с частотой – 100 Гц. Линия, проведенная через приемник и источник, нормальна к стенке, которая движется к источнику вдоль этой линии со v= 7 м/с. Скорость звука 340 м/с. Возможно ли возникновение акустического биения.
Для рецензии и заметок:
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Видео:Продольные и поперечные волныСкачать
Продольные и поперечные волны
Отвлечемся от внутреннего строения вещества для того, чтобы исследовать законы распространения механических волн. Вещество будем рассматривать как сплошную среду, непрерывно изменяющуюся в пространстве.
Частицей, изучая колебания, будем называть малый элемент объема среды, размеры которого много больше, чем расстояния между молекулами, при этом частицу среды принимаем за материальную точку.
Рассматривая механические волны, будем считать вещества, в которых они распространяются, упругими, внутренние силы, возникающие в них при малых деформациях, пропорциональными величине деформации.
При возбуждении колебания, в каком- либо месте упругой среды, в результате взаимодействия частиц среды, оно распространяется в веществе от точки к точке с некоторой конечной скоростью. Процесс распространения колебаний называют волной. Важным свойством волнового процесса является то, что в нем не происходит переноса массы, каждая частица выполняет колебания около положения равновесия. В волне от частицы к частице передается состояние колебательного движения и энергия колебаний. Волна переносит энергию.
В зависимости от направления колебаний частицы вещества по отношению к направлению распространения волны, волны делят на продольные и поперечные.
Видео:🌊 Продольные и поперечные волны ⚛ ФизикаСкачать
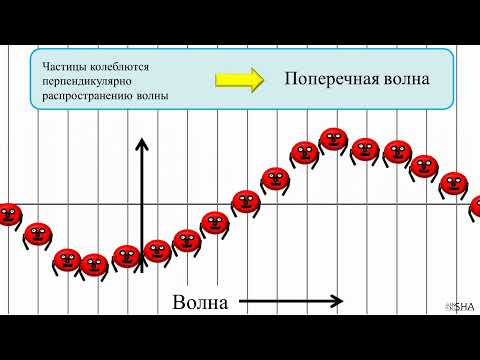
Продольные волны
Если частицы совершают колебания в направлении распространения волны, то такую волну называют продольной.
Продольные волны распространяются в веществе, в котором возникают силы упругости, при деформации растяжения и сжатия в веществе в любом агрегатном состоянии.
Так, например, волны звука, распространяющиеся в воздухе, относят к продольным волнам. Продольные волны, имеющие частоты от 17 до 20
000 Гц называют звуковыми. Скорость распространения акустических волн зависит от свойств среды и ее температуры.
При распространении продольной волны в среде возникают чередования сгущений и разрежений частиц, перемещающихся в направлении распространения волны со скоростью $v$. Все время существования волны, элементы среды выполняют колебания у своих положений равновесия, при этом разные частицы совершают колебания со сдвигом по фазе. В твердых телах скорость распространения продольных волн больше, чем скорость поперечных волн.
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (1) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа.
Скорость распространения продольных волн в тонком стержне, вызванных его продольным растяжением и сжатием равна:
где $E$ — модуль Юнга вещества стержня.
Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Поперечные волны
Поперечной волной называют такую волну, в которой колебания частиц среды происходят в направлениях перпендикулярных к направлению распространения волны.
Механические волны могут быть поперечными только в среде, в которой возможны деформации сдвига (среда обладает упругостью формы). Следовательно, в жидкостях и газах механических поперечных волн не наблюдают. Поперечные механические волны возникают в твердых телах. Примером таких волн являются волны, которые распространяются в натянутых струнах.
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
где $G$ — модуль сдвига среды; $rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Приведенная здесь скорость распространения упругих волн называется фазовой скоростью.
Видео:Физика 11 класс (Урок№2 - Механические волны.)Скачать

Уравнение продольной и поперечной волны
Основной задачей при изучении волн является установление закона изменения во времени и пространстве физических величин, которые однозначно характеризуют движение волны. При рассмотрении упругих волн такой величиной служит, например, смещение ($s$) частиц среды от их положений равновесия. Функция $s$ в зависимости от координат пространства и времени называется уравнением волны.
Самым простым видом волн являются гармонические волны. В таких волнах параметры $s$ для всех частиц среды, которые охвачены волной, совершают гармонические колебания с одинаковыми частотами. Для реализации данного волнового процесса необходимо, чтобы источник гармонических волн совершал незатухающие гармонические колебания.
Уравнение одномерной волны записывают как:
$k$ — волновое число; $lambda $ — длина волны; $A$ — амплитуда волны в точке (если среда не поглощает энергию, то амплитуда колебаний совпадает с амплитудой колебаний источника волн); $left[omega t-kx+varphi right]$ — фазой волны; $omega $- циклическая частота колебаний; $varphi $ — начальная фаза.
Видео:Механические модели волн. 1.Скачать

Примеры задач с решением
Задание: Поперечная волна распространяется по натянутой струне со скоростью $v=2frac$, период колебаний точек струны равен T= 1 с, амплитуда колебаний составляет 0,05 м. Какими будут смещение и скорость малого элемента струны, который находится на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c?
Решение: Основой для решения задачи служит уравнение одномерной волны:
где $s$ — смещение точки струны, совершающей колебания; $x$ — расстояние от источника волны до рассматриваемой точки; $k=frac$ — волновое число; $v$ — скорость распространения волны.
Циклическую частоту $omega $ найдем (при T=1 c) как:
Тогда волновое число при $v=2frac$ равно:
Уравнение для нашей волны в учетом данных задачи приобретет вид:
Смещение точки струны, находящейся на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c будет равно:
Скорость рассматриваемой точки струны найдем как:
Ответ: $s_1=-0,05$ м; $frac
Задание: Плоская одномерная волна распространяется в упругой среде. Изобразите на графике направление скорости частиц среды в точках $s=0, $при t=0 для продольной и поперечной волн.
Решение: Уравнением одномерной плоской волны служит выражение:
При $t=0 c$ из выражения (2.1) получаем:
В продольной волне частицы смещаются вдоль направления скорости движения волны (рис.1).
В продольной волне частицы совершают колебания поперек направления скорости движения волны рис.2.
📹 Видео
Упругие механические волны. 1 часть. 11 класс.Скачать

Волновое уравнение для волн в упругой среде.Скачать

Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Физика 9 класс. §28 Распространение колебаний в среде. ВолныСкачать

Уравнения математической физики. Одномерное волновое уравнениеСкачать

Урок 95 (осн). Механические волны. ЗвукСкачать

74. Упругие волныСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Лекция 2 ВолныСкачать

5.6 Механические волны. Виды волнСкачать
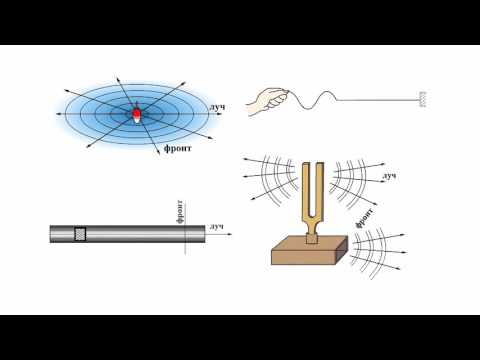
Распространение колебаний в упругих средах Продольные и поперечные волны convertedСкачать

Физика 9 класс (Урок№12 - Волновые явления. Длина волны. Скорость распространения волн.)Скачать

Получение уравнения плоской бегущей волны.Скачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать