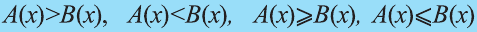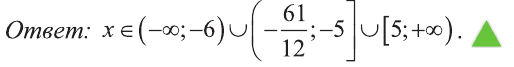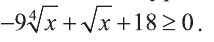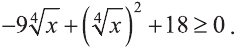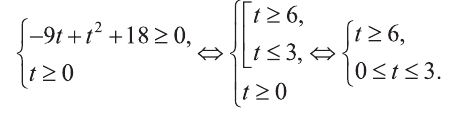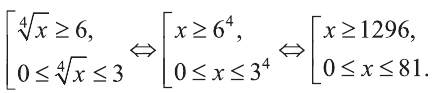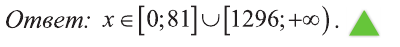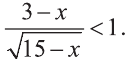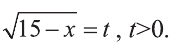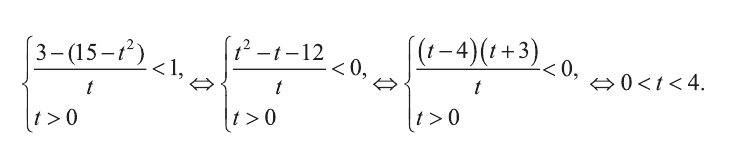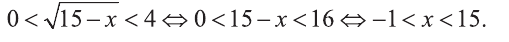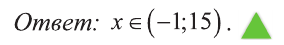Неравенство квадратное уравнение в знаменателе

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

1. Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

1. Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя .

1. Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя .

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

1. Нанести нули числителя и нули знаменателя на ось x .

Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые .

Если знак неравенства строгий ,
при нанесении на ось x нули числителя выколотые .

Если знак неравенства нестрогий ,
при нанесении на ось x нули числителя жирные.

1. Расставить знаки на интервалах.

1. Выбрать подходящие интервалы и записать ответ.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

1. Приравниваем числитель к нулю f ( x ) = 0.

x = 1 – это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

1. Приравниваем знаменатель к нулю g ( x ) = 0.

x = − 3 – это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x .

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Привести неравенство к виду f ( x ) g ( x ) ≤ 0.

3 ( x + 8 ) − 5 x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

− 5 x − 37 x + 8 ≤ 0

1. Приравнять числитель к нулю f ( x ) = 0.

x = − 37 5 = − 37 5 = − 7,4

x = − 7,4 – ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

1. Приравнять знаменатель к нулю g ( x ) = 0.

x = − 8 – это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x .

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

1. Приравнять числитель к нулю f ( x ) = 0.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

x 1 = 1, x 2 = − 1 – нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

1. Приравнять знаменатель к нулю g ( x ) = 0.

x = 0 – это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x .

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Если вас интересуют более сложные неравенства (с корнем чётной степени кратности, например), посмотрите видео «Метод интервалов: сложные случаи».

Спасибо за просмотр этого урока! Если у вас остались вопросы, напишите их в комментариях.

Видео:Решение квадратных неравенств | МатематикаСкачать

Квадратные неравенства. Как решать квадратные неравенства?

Квадратными неравенствами называют неравенства, которые можно привести к виду (ax^2+bx+c) (⋁) (0), где (a),(b) и (с) — любые числа (причем (a≠0)), (x) – неизвестная переменная, а (⋁) – любой из знаков сравнения ((>),( к вадратные уравнения , но со знаком сравнения вместо знака равно.
Примеры:

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Как решать квадратные неравенства?

Квадратные неравенства обычно решают методом интервалов . Ниже приведен алгоритм, как решать квадратные неравенства с дискриминантом больше нуля. Решение квадратных неравенств с дискриминантом равным нулю или меньше нуля – разобраны отдельно.

Приведите неравенство к виду (ax^2+bx+c⋁0).
Примеры:

(x^2-6x-16 корни (x_1) и (x_2). Затем запишите исходное выражение в виде (a(x-x_1 ) (x-x_2 )) Подробнее об этом можно почитать здесь .

(x^2-6x-16=0) (-9x^2+x+8=0)
(D=36-4 cdot 1 cdot (-16)=100=10^2) (D=1-4 cdot (-9) cdot 8=289)
(x_1=frac=-2) (x_1=frac=frac=-frac) (x_2=frac=8) (x_2=frac=frac=1)
((x-8)(x+2) )) то точки должны быть выколоты, если неравенство нестрогое (со знаком (≤) или (≥)), то точки должны быть закрашены.

Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
(-) знак плюс если перед скобками ничего не стоит или стоит положительное число
(-) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки.

Заштрихуйте подходящие интервалы, то есть числовые промежутки :
(-) со знаком «(+)», если в неравенстве стояло «(>0)» или «(≥0)»
(-) со знаком «(-)», если в неравенстве стояло «( )) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде ((x_1;x_2)) – скобки круглые. При нестрогих знаках неравенства ((≤) или (≥)) — границы интервала ВХОДЯТ в решение, и ответ записывается в виде ([x_1;x_2]), с квадратными скобками на точках.

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Рациональные неравенства и их системы с примерами решения

Содержание:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Простые рациональные неравенства и их системы

Рациональные неравенства одной переменной и методы их решения

Пусть А(х) и В(х) — рациональные выражения. Отношения вида

Пример:

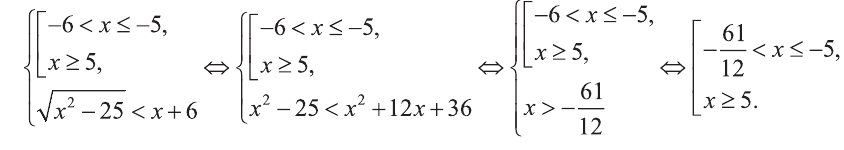
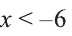
Решите неравенство: 2(2х-5)(Зх-8)(5-4х) 0, то мы можем возвести обе части заданного неравенства в квадрат: При заданное неравенства обязательно выполняется:

Замена переменной

Этот метод аналогичен соответствующему методу замены переменной, использованному при решении иррациональных уравнений.

Пример:

Решите неравенство:

Решение:

Выпишем неравенство в виде:

Введем новую переменную: 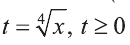В этом случае

Значит:

Пример:

Решите неравенство:

Решение:

Введем новую переменную:

Отсюда, 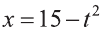и получим рациональное неравенство от переменной t:

Из последнего неравенства найдем х:

• Геометрические задачи и методы их решения
• Прямые и плоскости в пространстве
• Интеграл и его применение
• Первообразная и интегра
• Перпендикулярность в пространстве
• Векторы и координаты в пространстве
• Множества
• Рациональные уравнения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📸 Видео

Решение неравенства методом интерваловСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Метод интервалов #3Скачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать

Как решать неравенства? 9 - 11 класс. Вебинар | Математика TutorOnlineСкачать

Неравенства с модулем | Математика | TutorOnlineСкачать

Классический способ решения рациональных неравенств #ShortsСкачать

Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать