Неоднородное уравнение колебаний струны пример (6 видео)

Содержание

Лекция 2. Вывод уравнения колебания струны
Начальные условия и граничные условия.
Электронная библиотека
🔥 Видео

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Лекция 2. Вывод уравнения колебания струны

Рассмотрим струну длины l

Струной будем называть тонкую туго натянутую упругую нить.

При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).

Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной U_x.

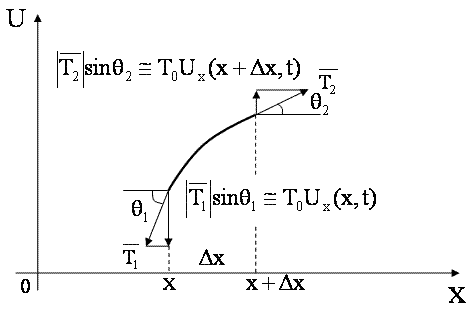
Рис. 3

Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной U_x 2 можно пренебречь). С ледовательно, в соответствии с законом Гука _.

Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .

Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)

При выводе этой формулы учитываем, что при малых колебаниях

По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=U_tt, поэтому

ρ ∆ xU_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]+ γ ( x , t ) ∆ x .

Разделим обе части равенства на Δx и устремим Δx к нулю:

ρ ( x ) U_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]/ ∆ x + γ ( x , t ) .

Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде

U_tt = a 2 U_xx + f ( x , t ),где a 2 = T ₀/ ρ ; f ( x , t )= γ ( x , t ) / ρ .

В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны

Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).

Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.

Начальные условия и граничные условия.

Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.

Для волнового уравнения U_tt = a 2 U_xx задаются два начальных условия U | _{t =0} = φ ( x ), U_t | _{t =0} = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), U_t ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения U_tt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.

Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | _{x =0} = 0, U | _{x = l} = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, U_x |_х=0= 0 , U_x |_х= _l = 0. Такие условия возникают в следующей задаче.

Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).

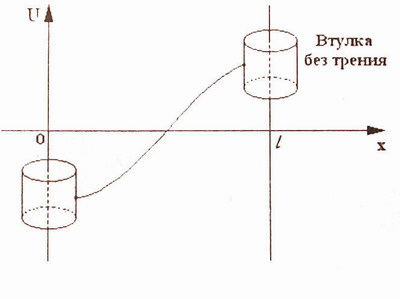
рис.4

Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T ₀ U_x ( O , t ) и T ₀ U_x (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).

Как было уже сказано, волновое уравнение U_tt = a 2 U_xx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:

Граничные условия (5), (6) и (7) называются однородными, если правые части g₁(t) и g₂(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.

Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .

К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|_Γ=О, в пространстве U|_Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.

При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), U_t (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.

Видео:Неоднородное уравнение колебания струныСкачать

Электронная библиотека

Здесь мы покажем, как применяются ряды Фурье при решении задачи о колебании струны. Под струной мы понимаем тонкую гибкую нить, не оказывающую сопротивления изгибу.

Рассмотрим струну, которая в начальный момент совмещена с отрезком оси Ох. Будем считать, что концы х = 0 и x = l закреплены на оси Ох. Пусть струна растягивается силами и , приложенными к её концам и направленными вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить самой себе, под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдет дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна станет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.

Сделаем ряд предположений. Во-первых, считаем, что, выводя струну из состояния равновесия, мы придаем ей форму некоторой линии. Поскольку концы струны закреплены на оси Ох, то на функцию U(x) линии надо наложить требования U(0) = U(l) = 0. Во-вторых, будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. В-третьих, колебания предположим малыми, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во все время движения струна будет сохранять пологую (гладкую) форму, это значит, что угол , образуемый касательной к струне с осью Ох, мал, чтобы можно было считать . Наконец, считаем струну однородной, причем массу единицы длины струны в её нерастянутом состоянии считать равной её плотности .

Возьмем какую-либо точку струны, имевшую в начальный момент t = 0 абсциссу х. Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса х не будет меняться. Ордината её у будет зависеть от времени, а также от того, о какой точке идет речь, а именно от абсциссы х этой точки, т.е. ордината будет функцией от х и t. Эту функцию в дальнейшем будем обозначать через U(x, t). Ясно, что она должна удовлетворять граничным условиям:

и начальным условиям:

первое из (4.10) выражает, что струне придана форма, а второе означает, что точки струны имеют начальные скорости (мы, предположим, что ).

Переведем физическую задачу на язык математики, т.е. выведем дифференциальное уравнение, которому должна удовлетворять искомая функция U(x,t). Для этого выделим на струне элементарный участок, который при t = 0 совпадает с отрезком [x,x+dx] оси Ох. В момент t это будет дуга линии U(x ,t). Длина этой дуги:

пренебрегая (мы сделали допущение, что ), получим: ds = dx (т.е. струна не растягивается). Масса выделенного участка равна: . К этому элементу будут приложены растягивающие его силы. Пусть натяжение в точке х будет равно . Тогда к концам нашего элемента будут приложены силы и .

Они направлены по касательным в этих точках. Обозначим через и соответствующие углы в точках струны (рис. 4.1). Обозначим равнодействующую сил, приложенных к концам элемента, через , а ускорение элемента через . Тогда векторное уравнение движения элемента имеет вид:

Спроектируем это уравнение на ось Ох, находим:

( означает проекцию силы на ось Ох, а – численные значения натяжения в точке, абсцисса которой х).

Поскольку точки струны движутся перпендикулярно оси Ох, то , стало быть . Но

так как . Сопоставляя это с равенством , находим, что . Это значит, что величина натяжения не меняется вдоль струны. Но, так как на концах струны это натяжение есть , вместо F_x, F_x₌_dx будем писать: .

Спроектируем уравнение (4/11) на ось Оу:

Так как , а то (4.13) дает:

Тогда уравнение будет иметь вид:

где . Уравнение (4.14) называется уравнением свободных колебаний струны или волновым уравнением.

Таким образом, механическая задача свелась к чисто математической (получили математическую модель процесса колебания струны): найти такое решение уравнения (4.14), которое удовлетворяет начальным и граничным условиям (4.9) и (4.10). Существуют разные способы решить эту задачу. Один из способов был предложен в XYIII веке Д. Бернулли. Позже, уже в XIX веке, этот способ систематически применялся Фурье для решения целого ряда термодинамических задач, почему он и получил название метода Фурье. Этот способ мы рассмотрим далее. Он требует сначала решения одной важной задачи, которая носит название задачи о собственных значениях и собственных функциях. Однако решим одну вспомогательную задачу: найти функцию U = U(x, t), удовлетворяющую требованиям:

Отличие этой задачи от той, которую нам надо решить, состоит в том, что от искомой функции U(x ,t) мы не требуем, чтобы она удовлетворяла начальным условиям где , но зато требуем, чтобы она имела специальный вид X(x)T(t) и была отличной от тождественного нуля.

Измененная задача решается довольно просто и имеет бесконечное множество решений, из которых удается составить и решение нашей основной задачи.

Итак, пусть имеем первое условие (4.15).

Из него вытекает, существование такой точки , что . Тогда , т.е. . Подставим в граничные условия:

Отсюда видно, что искомая функция X(x) должна удовлетворять условиям:

Подставляя из четвертого условия (4.15.) во второе, получим:

Обратим внимание, на то, что правая часть (4.15) не зависит от . Следовательно, и левая часть от не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного , ибо . Значит, левая (и правая) часть равенства должна быть постоянной величиной. Обозначим ее (пока неизвестную) через .

Допустим, что . Тогда из (4.17) следует . Отсюда и , т.е. должна быть линейной функцией. Подставляя в X(0 )= X(l) = 0, получим:

т.е. , а с ним и , что противоречит допущению первому из (4.15). Таким образом, не существует решения вспомогательной задачи для .

Допустим, что , т.е. , где можно считать положительным. Тогда

Общее решение этого уравнения имеет вид:

Решая эту систему, находим . Это приводит к , что противоречит первому условию (4.15). Итак, неравенство невозможно.

Пусть , т.е. , где . Тогда

Решив это уравнение, получим:

Граничные условия дают: . Заменяя на С, имеем , а второе условие дает . Это возможно лишь при . Значит, для возможны значения , что приводит к следующим выражениям для :

причем при каждом может принять любое (отличное от 0) значение. Заметим, что здесь решена задача о собственных значениях и собственных функциях. Поэтому числа и функции называются соответственно: собственными числами, а функции собственными функциями, которые соответствуют собственным числам (значениям).

Выбрав возможное значение , и подставив в (4/17), получим:

где А и В – произвольные постоянные. Обозначая Т буквой Т_n и полагая , , получаем бесконечное множество решений вспомогательной задачи:

Отметим, что наше уравнение и условия линейны и однородны, т.е. такие, что сумма функций , которая удовлетворяет им, также будет решением. Поэтому функция

при условии сходимости ряда также будет решением. Чтобы функция (4.22) была решением исходной задачи надо подобрать и так, чтобы выполнялись начальные условия (4.10).

Первое условие с (4.10) дает:

Дифференцируя (4.22), получим:

Чтобы удовлетворить соотношению (4.24), надо положить . Соотношение (4.23) говорит, что коэффициенты должны равняться коэффициентам разложения функции , заданной на [0,l], по функциям в ряд Фурье. Поэтому

Таким образом, искомое решение имеет вид

где определяется по (4.25).

1) Полученное решение носит формальный характер, так как мы не исследовали сходимость ряда (4.26). Однако можно показать, что если функция гладкая на [0,l], то ряд сходится и его сумма U(x,t) удовлетворяет исходному уравнению и начальным и краевым условиям.

2) Примененный метод решения задачи обычно называют методом Фурье или методом разделения переменных или методом собственных функций.

Решение (4.22) с учётом , можно записать в виде:

Каждый член этого ряда представляет собой так называемую стоячую волну, при которой точки струны совершают гармоническое колебательное движение с одинаковой фазой , с амплитудой и частотой .

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00