Для модели идеального смешения принимается ряд допущений. Допускается, что в результате интенсивного перемешивания устанавливаются абсолютно одинаковые условия в любой точке реактора: концентрации реагентов и продуктов, степени превращения реагентов, температура, скорость химической реакции и т. д. Например, в некоторый момент времени τj во всех точках ректора (рис. 5.1) выполняются следующие условия:
где x, у, z – пространственные координаты.
В проточном реакторе идеального смешения концентрации элементов реакции в выходном потоке в рассматриваемый момент времени τi строго равны концентрациям тех же веществ в реакторе.
Чтобы перечисленные допущения могли быть выполнены, необходимо принять еще одно допущение: переход от одной концентрации к другой в реакторе идеального смешения не должен иметь протяженности во времени. Изменение концентрации исходного реагента от начальной cJ,0 во входном потоке в данный момент времени τi до концентрации в реакторе сJ в этот же момент времени должно происходить мгновенно (скачкообразно).
Приблизиться к режиму идеального смешения можно, обеспечив интенсивное перемешивание реакционной смеси механическими мешалками разного типа или циркуляционными насосами, создающими высокую кратность циркуляции. Смешение, близкое к идеальному смешению, легче выполнить в емкостных аппаратах с приблизительно равным диаметром и высотой.
Так как в реакторе идеального смешения концентрации элементов реакции равномерно распределены по объему, то уравнение материального баланса (4.7), выведенное для элементарного объема, можно распространить на полный объем реактора.
Рассмотрим два частных случая: периодический реактор идеального смешения и проточный реактор идеального смешения, работающий в стационарном режиме.
Периодический реактор идеального смешения.В периодический реактор все реагенты вводят до начала реакции, а все продукты выводят из него только по окончании процесса. В ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, изменяется лишь ее состав. При составлении математического описания принимают, что реакционная смесь однородна по объему аппарата и ее состав зависит только от времени пребывания в периодическом реакторе.
Рис. 5.1. Схемы реакторов идеального смешения
с механическим перемешивающим устройством (а)
и циркуляционным контуром (б)
Из общего уравнения материального баланса (4.7) в случае периодического реактора идеального смешения можно исключить два первых оператора, описывающих явления конвективного и диффузионного переноса вещества в аппарате. При отсутствии перемещения потока через реактор в произвольный момент времени между началом и окончанием процесса средняя линейная скорость элемента потока равна нулю, следовательно, и конвективный перенос в непроточном реакторе отсутствует. Заключение об отсутствии диффузионного переноса вытекает из допущений модели идеального смешения, так как диффузия возможна лишь при наличии градиента концентраций, а при равномерном распределении концентраций по объему он равен нулю. (Этот вывод справедлив не только для периодического, но и для проточного реактора идеального смешения.)
Следовательно, уравнение материального баланса для периодического реактора идеального смешения примет вид
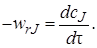
В уравнении (5.1) частная производная заменена на полную, так как в соответствии с допущениями идеального смешения концентрация с внутри реактора является функцией только одной переменной – времени.
Уравнение материального баланса периодического реактора идеального смешения (5.1) совпадает с уравнением (3.2), дающим определение скорости химического превращения. Из одинакового вида уравнений косвенно можно сделать вывод, что гидродинамическая обстановка в периодическом реакторе идеального смешения не накладывает ограничений на химическую кинетику.
Для проведения расчетов по уравнению (5.1) в его левую часть вместо wrJ(cJ)вводят конкретное кинетическое уравнение. Тогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации сJ,f):
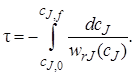
Если вещество J – исходный реагент, то концентрацию cs можно выразить через его степень превращения:
и уравнение (5.2) примет вид
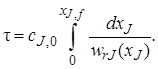
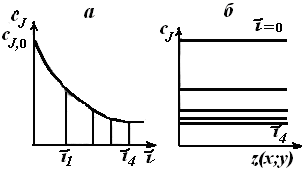
Уравнения (5.2) и (5.3) позволяют также рассчитать зависимость концентрации реагента сJ или его степени превращения хJ от времени пребывания в реакторе (продолжительности реакционного цикла). В разные моменты времени условия в периодическом реакторе различные (концентрация реагентов, продуктов, скорость реакции и т. д.), однако в каждый данный момент времени из-за допущения об идеальности эти параметры строго одинаковы в объеме реактора (рис. 5.2).
Время, рассчитанное по уравнению (5.2) или (5.3), является «чистым» временем, необходимым для проведения химического превращения. Однако для осуществления процесса в периодическом реакторе кроме этого «реакционного» времени нужно затратить вспомогательное время на загрузку реагентов, выведение реактора на нужный технологический режим, разгрузку и очистку. Полное время одного цикла работы периодического реактора суммируется из основного τхр и вспомогательного τвсп.
Рис. 5.2. Изменение концентрации исходного реагента
в периодическом реакторе идеального смешения во времени (а)
и по объему аппарата (б)
Наличие τвсп как составной части времени цикла приводит к снижению производительности химического реактора (количество продукта, получаемого в единицу времени) и является одним из существенных недостатков периодических процессов вообще. Другие их недостатки – большие затраты ручного труда, сложность решения задач автоматизации (так как условия в реакторе во времени постоянно меняются).
Однако периодические реакторы обычно можно приспособить к широкому диапазону условий реакций, что удобно при необходимости производить на одной установке различные химические продукты, например, в промышленности химических реактивов.
Периодические реакторы с интенсивным перемешиванием, приближающимся к идеальному смешению, применяют в производствах реактивов, органических красителей, лекарственных препаратов – там, где для достижения достаточной глубины превращения требуется сравнительно длительное время, а объемы производства невелики.
Периодические реакторы смешения часто применяют в микробиологической промышленности для культивирования аэробных микроорганизмов. Процесс культивирования для большинства микроорганизмов длится 48–72 ч, т. е. достаточно длителен. Интенсивное перемешивание в ферментаторе позволяет обеспечить равномерное распределение температуры, что особенно важно в таких процессах, так как даже небольшие локальные разогревы могут привести к гибели микроорганизмов. Изолированность реакционной системы в периодическом реакторе позволяет устранить опасность отравления микроорганизмов случайными примесями, которые могут попасть в аппарат при непрерывной подаче реагентов.
Окончательное решение о целесообразности применения периодического или непрерывного процесса можно вынести лишь на основании экономической оценки (сравнения расходов на эксплуатацию, амортизацию, электроэнергию, пар, сырье и т. д.). Как правило, при проведении такого сравнения оказывается, что периодические процессы выгодны при относительно невысокой производственной мощности в тех случаях, когда получают дорогостоящие продукты.
Проточный реактор идеального смешения в стационарном режиме.Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме.
Рассмотрим уравнение материального баланса для стационарного проточного реактора идеального смешения без циркуляции. Получим его, опять упрощая общее уравнение материального баланса (4.7). Для любого реактора идеального смешения, и в частности для проточного, из уравнения можно исключить оператор, описывающий диффузионный перенос. При стационарном режиме работы реактора из уравнения исключается производная дсJ/дτ,не равная нулю только при наличии накопления вещества в реакторе.
Таким образом, в уравнении остаются только два члена, описывающие конвективный перенос вещества J и расход или образование этого вещества в ходе химической реакции.
Оператор конвективного переноса (переноса импульса), записанный в уравнении (4.7) в дифференциальной форме, можно представить для проточного реактора идеального смешения в конечно-разностной форме. В соответствии с допущениями модели идеального смешения в проточном реакторе происходит дискретное конечное (а не бесконечно малое) изменение концентрации ∆сJ сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации ∆сJ к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью 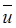
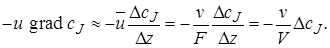
В выражении (5.4) ∆сJ равно разности концентраций на выходе из реактора cif и на входе в реактор сJ,0. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
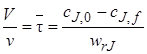
Это же уравнение можно получить и другим путем. Как указывалось, в качестве элементарного объема для реактора идеального смешения можно принять полный объем реактора V. При стационарном режиме работы реактора не происходит изменения постоянных по объему концентраций элементов реакции и во времени, следовательно, в качестве элементарного промежутка времени можно принять любой конечный временной интервал, например единицу времени (1 с, 1 мин или 1 ч).
Количество вещества J, которое за единицу времени войдет в реактор с конвективным потоком, будет равно v0cJ,0,где v0 – объемный расход реакционного потока на входе в аппарат. За это же время выйдет из реактора с конвективным потоком количество вещества J = vfcJ,f,а расход вещества J (или его образование) в ходе химической реакции составит wrJ V. При этом скорость wrJ определяется концентрацией cJ,f.
Стационарность процесса в проточном реакторе можно обеспечить, если объемные расходы на входе v0 и выходе vf равны между собой
(v0 = vf = v).
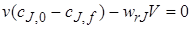
Очевидно, что уравнение (5.6) тождественно уравнению (5.5).
Величина 
Действительное время пребывания частиц в проточном реакторе смешения является случайной величиной в отличие от времени пребывания реагентов в периодическом реакторе. Пусть, например, в реактор введено N одинаковых частиц. В периодическом реакторе все они будут находиться равное время от загрузки до выгрузки. В проточном реакторе идеального смешения эти частицы мгновенно и равномерно распределяются по всему объему аппарата, и так как из аппарата непрерывно выходит поток продуктов, то в момент ввода частиц в реактор какое-то их количество может сразу же оказаться в выходном потоке. Некоторые частицы, равномерно распределяясь в новых порциях реакционной смеси, вошедшей в аппарат, могут находиться в нем бесконечно долго. Отсюда можно сделать вывод, что действительное время пребывания частиц в проточном реакторе – это случайная величина, которая может изменяться от 0 до ∞. Непрерывную случайную величину можно задать с помощью вероятностных характеристик, в частности функций распределения случайной величины. Использование в качестве характеристики времени пребывания частиц в проточном реакторе величины 
Для решения практических задач удобно концентрацию реагента cJ,fвыразить через его степень превращения хJ,f:
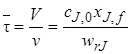
Уравнения материального баланса (5.5)–(5.7) для проточного реактора идеального смешения в стационарном режиме имеют ряд отличий от соответствующих уравнений для периодического реактора (5.2) и (5.3). Следует отметить, что балансовые уравнения стационарного реактора идеального смешения записываются сразу в виде конечного алгебраического уравнения в отличие от дифференциальной формы исходных уравнений для периодического реактора.
В уравнение для периодического реактора скорость wr,Jследует подставлять в виде функциональной зависимости от концентрации wr,J(cj) или степени превращения wr,J(xj) и лишь после интегрирования уравнения возможна подстановка числовых значений. Этот факт, как и дифференциальная форма уравнений материального баланса, отражает зависимость параметров процесса в периодическом реакторе от времени. В стационарном режиме в любой точке реактора идеального смешения в любой момент времени концентрация постоянна. Следовательно, скорость реакции характеризуется каким-то одним конкретным числовым значением, определяемым этой концентрацией. Это число может быть сразу поставлено в уравнение материального баланса.
Пример 5.1.Рассчитать среднее время пребывания реагентов в проточном реакторе идеального смешения, необходимое для достижения степени превращения исходного реагента хА,f= 0,8.
В реакторе протекает реакция второго порядка 2А 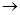
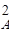
Решение. Для определения 
Таким образом, для достижения степени превращения хА = 0,8 необходимо, чтобы соотношение между объемом реактора и объемным расходом через него 
Уравнения материального баланса для проточного реактора могут быть использованы не только для определения среднего времени пребывания 

Решение этой задачи не вызывает никаких затруднений, если скорость реакции описывается сравнительно простыми кинетическими уравнениями (уравнениями первого и второго порядка). Например, для реакции первого порядка А 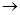
Зачастую скорость сложных реакций с невыясненным до конца механизмом выражают в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным и приходится прибегать к численным методам расчета. В качестве примера рассмотрим весьма наглядный графический метод определения концентрации реагентов на выходе из стационарного проточного реактора идеального смешения.
Запишем уравнение материального баланса (5.5) в следующем виде:
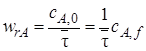
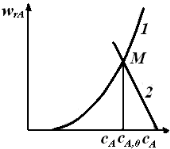
Уравнение (5.8) представляет собой равенство двух разных функций от концентрации. В левой части уравнения записана функция wrА(сА), представляющая собой кинетическое уравнение реакции. В соответствии с законом действующих масс скорость химических реакций пропорциональна концентрациям реагентов, следовательно, wrA(cA) – это возрастающая функция, которую легко представить графически (рис. 5.3, линия 1). Она пересекает ось абсцисс в точке, соответствующей равновесной концентрации сА,е для обратимых реакций, или исходит из начала координат в случае необратимых реакций.
Рис. 5.3. Зависимость скорости реакции от концентрации реагента
на выходе из проточного реактора идеального смешения,
используемая для определения конечной концентрации
В правой части уравнения (5.8) записана соответствующая уравнению материального баланса стационарного реактора идеального смешения линейная функциональная зависимость скорости реакции от концентрации исходного реагента, имеющая отрицательный угловой коэффициент (–1/ 
Уравнению (5.8) удовлетворяют такие значения концентраций сА, при которых значения функций, стоящих в левой и правой частях этого уравнения, равны. Иначе – такие концентрации, при которых графики этих функций пересекаются. Как видно, линии 1 и 2 пересекаются в единственной точке М.Абсцисса этой точки и есть искомая концентрация реагента на выходе из реактора идеального смешения.
Дата добавления: 2015-06-17 ; просмотров: 7957 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Модели реакторов идеального вытеснения и идеального смешенияСкачать

Виды химических реакторов. Реакторы идеального смешения и идеального вытеснения
ТЕМА 4 . Химические реакторы
План лекции:
4.1 Виды химических реакторов. Реакторы идеального смешения и идеального вытеснения.
4.2 Реакторы для гомогенных процессов
4.3. Реакторы для гетерогенных процессов с твердой фазой
4.4. Реакторы для газо-жидкостных процессов
Химический реактор – устройство, предназначенное для проведения в нём химических превращений.
Химический реактор – понятие обобщённое, относится к реакторам, колоннам, башням, автоклавам, камерам, печам, контактным аппаратам, полимеризаторам, дожигателям, гидрогенизаторам, окислителям и другим аппаратам, названия которых происходят из-за их назначения или даже внешнего вида.
Виды химических реакторов. Реакторы идеального смешения и идеального вытеснения
При классификации реакторов принимают во внимание следующие основные признаки:
1) характер операции, протекающей в реакторе;
2) режим движения реакционной среды;
3) тепловой режим;
4) фазовое состояние реагентов.
По первому признаку реакторы делят на периодические, непрерывные и полунепрерывные. Реакторы непрерывные, т.е. с непрерывной подачей реагентов и отводом продуктов, в свою очередь, подразделяются по характеру движения реакционной среды (т.е. по гидродинамической обстановке в реакторе) на реакторы идеального вытеснения и реакторы идеального смешения.
Реакторы периодическиехарактеризуются единовременной загрузкой реагентов. При этом процесс складывается из трех стадий: загрузки сырья, его обработки (химическое превращение) и выгрузки готового продукта. После завершения последовательности этих стадий они повторяются вновь, т.е. работа реактора осуществляется циклически. Продолжительность одного цикла, проводимого в периодическом реакторе, определяется по уравнению
где τп – полное время цикла; τ – рабочее время (затрачиваемое на проведение химической реакции); τвсп – вспомогательное время (загрузка реагентов и выгрузка продукта).
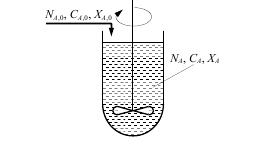
Реактор идеального смешения периодический представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты (рис. 4.1). В таком реакторе создается весьма интенсивное перемешивание, поэтому в любой момент времени концентрация реагентов одинакова во всем объеме реактора и изменяется лишь во времени, по мере протекания химической реакции. Такое перемешивание можно считать идеальным.
Рис.4.1 Реактор идеального смешения периодический
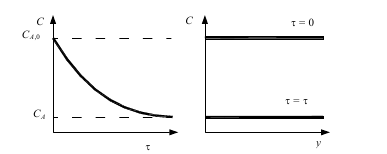
Изменение концентрации исходного реагента А во времени и в объеме реактора показано на рис. 10. Обозначения, приведенные на рис. 4.1 и 4.2 имеют следующие значения: NA,0, NA– количество исходного реагента Aв реакционной смеси в начале и конце процесса; CA,0, СA– начальная и конечная концентрации реагента Aв реакционной смеси; XA,0, XA – начальная и конечная степень превращения реагента A; τ – время; y – пространственная координата (координата места).
Рис. 4.2. Распределение концентрации реагента в периодическом реакторе идеального смешения: а) по времени, б) по месту ( по объему)
Периодические химические процессы по своей природе всегда являются нестационарными (неустановившимися), так как в ходе химической реакции параметры процесса изменяются во времени (например, концентрация веществ, участвующих в реакции, т.е. происходит накопление продуктов реакции). Реакторы периодического действия просты по конструкции, требуют небольшого числа вспомогательного оборудования, поэтому они особенно удобны для проведения опытных работ по изучению химической кинетики. В промышленности они обычно используются в малотоннажных производствах и для переработки относительно дорогостоящих химических продуктов. Большинство же промышленных процессов оформляется с использованием реакторов непрерывного действия.
В реакторах непрерывного действия (или проточных реакторах) питание реагентами и отвод продуктов реакции осуществляется непрерывно. Если в периодическом реакторе можно непосредственно, по часам, измерить продолжительность реакции, то в реакторе непрерывного действия этого сделать нельзя, так как при установившемся режиме в этих реакторах параметры не меняются со временем. В связи с этим для непрерывных реакторов применяют понятие условного времени пребывания реагентов в системе (времени контакта)
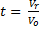
где Vr – объем реактора; V0 – объем реакционной смеси, поступающей в реактор в единицу времени (объемный расход реагентов).
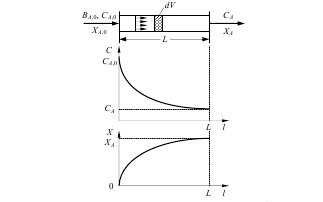
Реактор идеального вытеснения (РИВ) представляет собой трубчатый аппарат, в котором отношение длины трубы L к ее диаметру d достаточно велико. В реактор непрерывно подаются исходные реагенты, которые превращаются в продукты реакции по мере перемещения их по длине реактора (рис. 4.3). Гидродинамический режим в РИВ характеризуется тем, что любая частица потока движется только в одном направлении по длине реактора, обратное (продольное) перемешивание отсутствует; отсутствует также перемешивание по сечению реактора. Предполагается, что распределение вещества по этому сечению равномерное, т.е. значения параметров реакционной смеси одинаковые. Каждый элемент объема реакционной массы dVr движется по длине реактора, не смешиваясь с предыдущими и последующими элементами объема, и ведет себя как поршень в цилиндре, вытесняя все, что находится перед ним. Поэтому такой режим движения реагентов называется иногда поршневым или режимом полного вытеснения. Состав каждого элемента объема последовательно изменяется по длине реактора вследствие протекания химической реакции. Концентрация исходного реагента А постепенно меняется по длине реактора от начального значения CА,0 до конечного СА (рис.4.3). Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же. При составлении математического описания РИВ исходят из дифференциального уравнения материального баланса, преобразуя его с учетом указанных выше особенностей этого реактора. В реальном реакторе гидродинамическая обстановка отличается от обстановки в идеальном реакторе. Например, в реальном реакторе вытеснения, помимо поршневого движения основного потока по длине реактора, возможно перемешивание потока в продольном и радиальном направлениях. Степень отклонения показателей реального реактора от
Рис.4.3 Реактор идеального вытеснения и зависимости концентрации реагента СА и степени превращения ХА от длины реактора
идеального зависит от трех величин: коэффициента продольного перемешивания (конвективной диффузии) DL линейной скорости потока w и длины реактора L. Эти величины сведены в безразмерный комплекс DL/(wL).
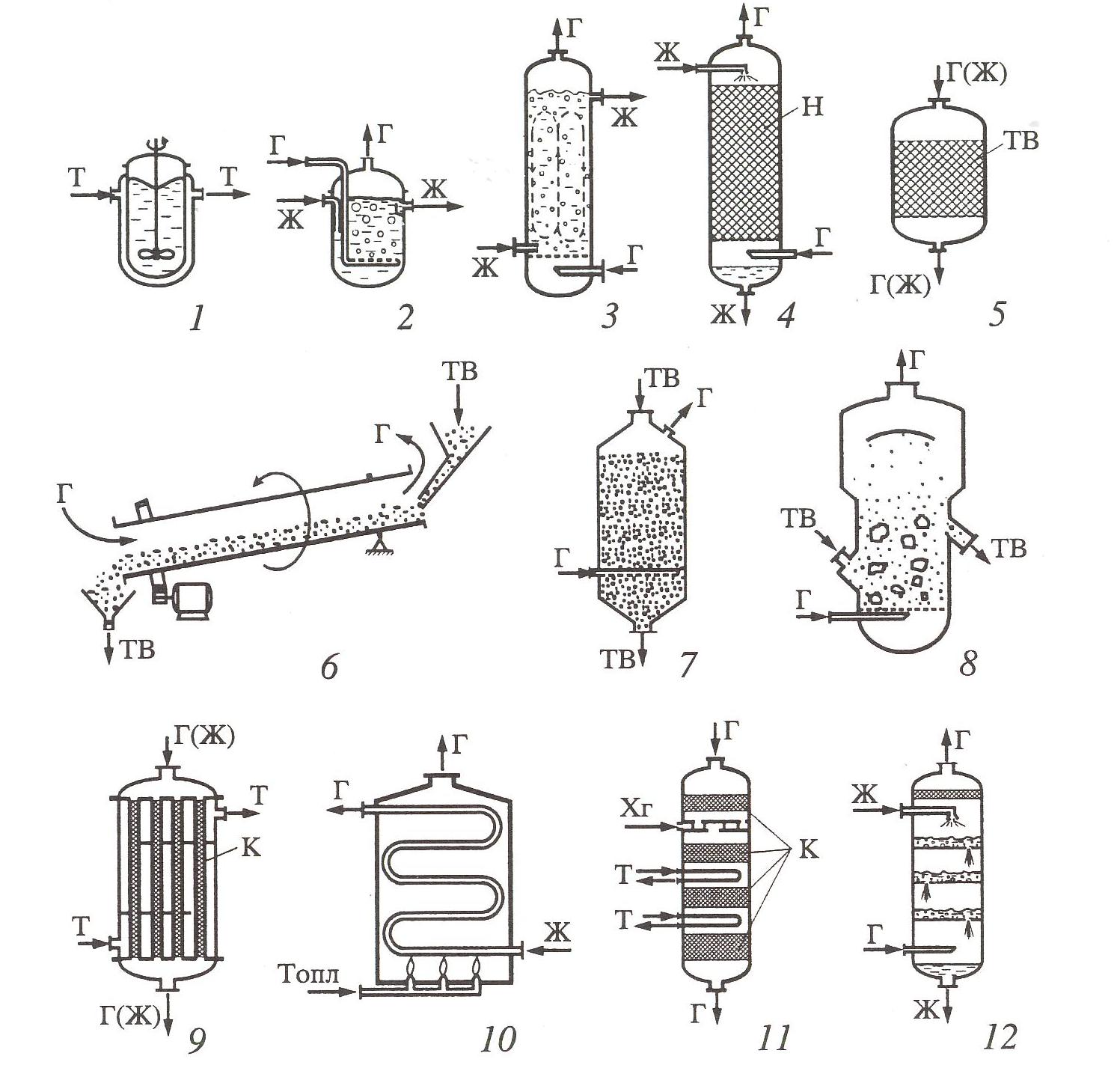
Общий вид реактора и схемы некоторых из них приведены на рис. 4.4.
Ёмкостный реактор 1 оснащён мешалкой, которая перемешивает реагенты (чаще жидкости, суспензии), помещаемые внутрь аппарата. Температурный режим поддерживается с помощью теплоносителя, циркулирующего в рубашке реактора или во встроенном в него теплообменнике. После проведения реакции продукты выгружают, и после очистки реактора цикл повторяется. Процесс периодический.
Ёмкостный реактор 2 является проточным, т.к. реагенты (чаще газ, жидкость, суспензия) непрерывно проходят через него. Газ барботирует через жидкость. Колонный реактор 3 характеризуется отношением высоты к диаметру, которое для промышленных реакторов составляет 4-6 (в емкостных реакторах это отношение около 1). Взаимодействие газа и жидкости такое же, как в реакторе 2.
Рис.4.4. Схемы химических реакторов:
Г – газ; Ж-жидкость; Т-теплоноситель; Н – насадка; ТВ – твердый реагент; К – катализатор; Хг –холодный газ; Топл. –топливо.
Насадочный реактор 4 оснащен кольцами Рашига или другими небольшими элементами – насадкой. Взаимодействуют газ и жидкость. Жидкость стекает по насадке, а газ движется между элементами насадки.
Реакторы 5-8 в основном используют для взаимодействия газа с твёрдым реагентом. В реакторе 5 твёрдый реагент неподвижен, газообразный или жидкий реагент непрерывно проходит через него. Процесс периодический по твёрдому веществу.
Ректоры 6-8 модифицированы таким образом, чтобы и по твёрдому реагенту процесс являлся непрерывным. Твёрдый реагент продвигается вдоль вращающегося наклонно установленного круглого реактора 6 или просыпается через реактор 7. В реакторе 8 газ подается снизу под большим давлением так, что твёрдые частицы оказываются во взвешенном состоянии, образуя псевдоожиженный или кипящий слой, обладающий некоторыми свойствами жидкости.
Трубчатый реактор 9 по виду подобен кожухотрубному теплообменнику. Через трубки, в которых протекает реакция, проходят газообразные или жидкие реагенты. Обычно в трубки загружен катализатор. Температурный режим обеспечивают циркуляцией теплоносителя в межтрубном пространстве.
Реакторы 5 и 9 используют также для проведения процессов на твёрдом катализаторе.
Трубчатый реактор 10 часто применяют для осуществления высокотемпературных гомогенных реакций, в том числе в вязкой жидкости (например, пиролиз тяжёлых углеводородов). Нередко такие реакторы называют печами.
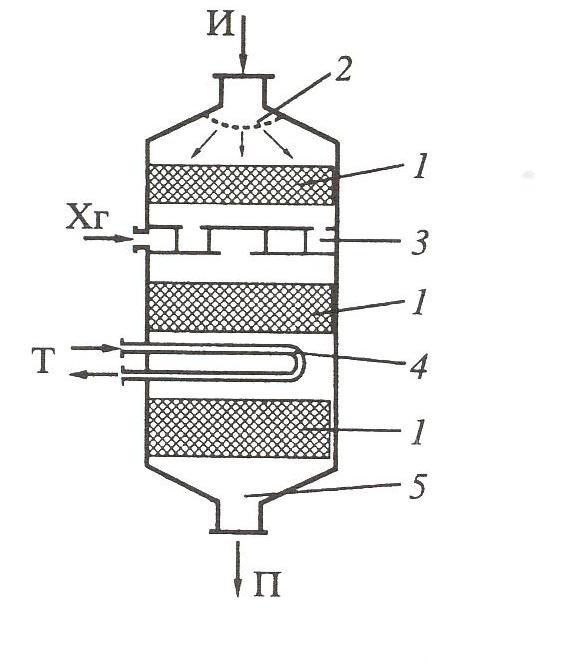
Многослойный реактор 11 оснащён системой, позволяющей охлаждать или нагревать реагент, находящийся между несколькими слоями твёрдого вещества, выполняющего роль, например, катализатора. На рисунке показано охлаждение исходного газообразного вещества холодным газом, введенным между верхними слоями катализатора, и теплоносителем через систему теплообменников, помещенных между другими слоями катализатора.
Многослойный реактор 12 предусмотрен для проведения в нём газожидкостных процессов.
Приведенные на рис 4.4 схемы отображают лишь часть применяемых в промышленности реакторов. Однако проведенная далее систематизация конструкций реакторов и протекающих процессов, позволяет разобраться и провести исследование в любом из них.
Для всех реакторов характерны общие структурные элементы, представленные в реакторе на рис. 4.5, аналогичном 11-му на рис.4.4.
Реакционную зону 1, в которой протекает химическая реакция, представляют несколько слоёв катализатора. Она есть во всех реакторах: в реакторах 1-3 на рис.4.4 – это слой жидкости, в реакторах 4, 5, 7 – слой
Рис. 4.5. Структурные элементы химического реактора:
1-реакционная зона; 2-входное и распределительное устройство; 3 – смеситель; 4 – теплообменник; 5 – выходное устройство; Хг –холодный газ; Т – теплоноситель; И и П – исходный и конечный продукты соответственно.
насадки или твёрдого компонента, в реакторах 6, 8 – часть объёма реактора с твёрдым компонентом, в реакторах 9, 10 – внутренний объём трубок, где протекает реакция.
Исходная реакционная смесь подаётся через верхний штуцер. Чтобы обеспечить равномерно распределённое прохождение газа через реакционную зону, обуславливающее однородный контакт реагентов, установлен распределитель потока. Это – устройство ввода 2. В реакторе 2 на рис. 4.4 распределителем газа является барботер, в реакторе 4 – разбрызгиватель.
Между первым сверху и вторым слоями два потока смешиваются в смесителе 3. Между вторым и третьим слоями помещен теплообменник 4. Эти структурные элементы предназначены для изменения состава и температуры потока между реакционными зонами. Теплообмен с реакционной зоной (отвод теплоты, выделяющейся в результате протекания экзотермических реакций или подогрев реагирующей смеси) осуществляется через поверхность встроенных теплообменников или через внутреннюю поверхность рубашки реактора (аппарат 1 на рис. 4.4), либо через стенки труб в реакторах 9, 10. Реактор может быть оснащён устройствами разделения потоков. Продукты выводятся через выходное устройство 5.
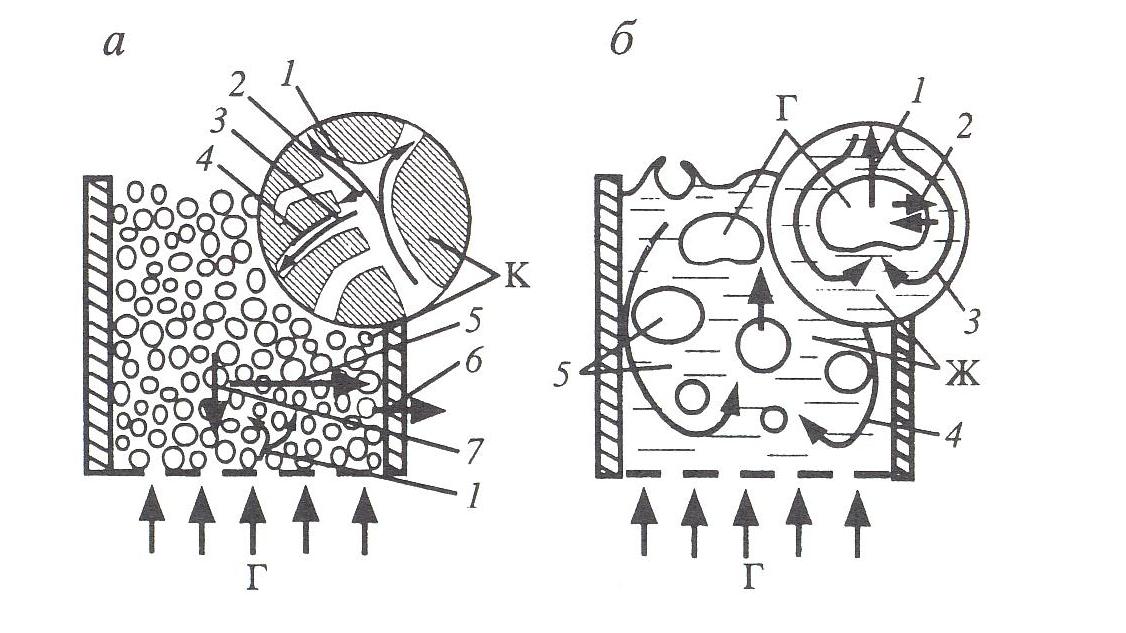
В теплообменниках и устройствах ввода, вывода, смешения, разделения, распределения потоков протекают физические процессы. Химические реакции осуществляются в основном в реакционных зонах, которые будут дальнейшим объектом исследования. Процесс, происходящий в реакционной зоне, представляет собой совокупность частичных этапов, которые схематически показаны на рис. 4.6 для каталитического и газожидкостного взаимодействия.
Рис.4.6. Схема потоков в каталитическом (а) и газожидкостном (б) процессах.
Рис.4.6,а представляет схему реакционного процесса с участием катализатора, через неподвижный слой которого проходит общий (конвективный) поток газообразных реагентов (1). Реагенты диффундируют к поверхности зерен (2) и проникают в поры катализатора (3), на внутренней поверхности которых протекает реакция (4). Образующиеся продукты реакции обратным путем отводятся в поток. Выделяющаяся в результате химического превращения теплота за счёт теплопроводности переносится по слою (5), а от слоя через стенку – к хладагенту (6). Возникающие градиенты концентраций и температуры вызывают дополнительные потоки теплоты и вещества (7) к основному конвективному движению реагентов в слое.
На рис.4.6,б представлен процесс в слое жидкости, через который барботирует газ. Между пузырями (1) газа и жидкостью происходит массообмен реагентами (2). Динамика жидкости складывается из движения около пузырей (3) и циркуляции в масштабе слоя (4). Первое – подобно турбулентной диффузии, второе аналогично циркуляционному конвективному движению жидкости через реакционную зону. В жидкости и, в общем случае, в газе протекает химическое превращение (5).
Приведенные примеры показывают сложную структуру процессов, протекающих в реакционной зоне. Если учесть множество схем и конструкций существующих реакторов, то разнообразие процессов в них многократно возрастает. Необходим научный метод, позволяющий систематизировать это многообразие, найти общность в нём, выработать систему представлений о закономерностях явлений и связей между ними, т.е. создать теорию химических процессов и реакторов.
Видео:Химические реакторыСкачать

Математические модели процессов в идеальных реакторах
Читайте также:
|
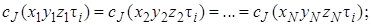
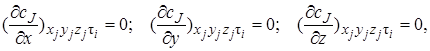
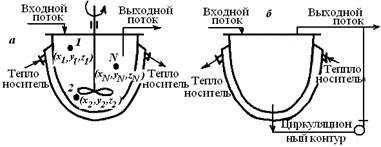
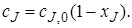
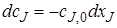
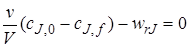
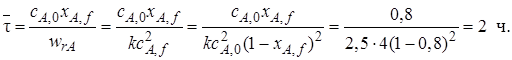
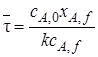
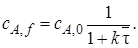
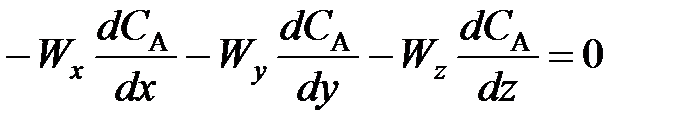 ; (77)
; (77)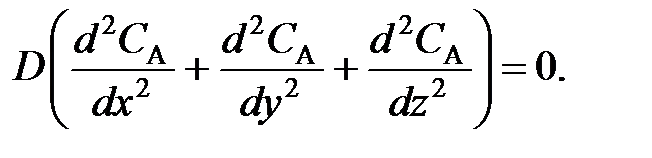 (78)
(78)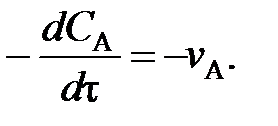 (79)
(79) . Поэтому перед
. Поэтому перед 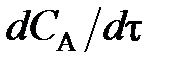 и vA ставят знак «–», чтобы скорость являлась положительной величиной.
и vA ставят знак «–», чтобы скорость являлась положительной величиной. (80)
(80)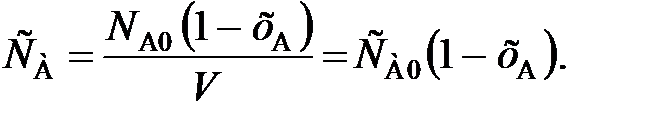 (81)
(81)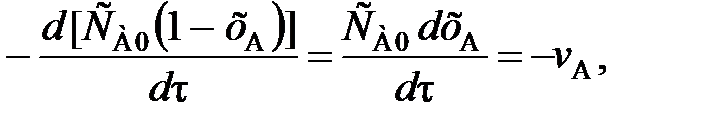 (82)
(82)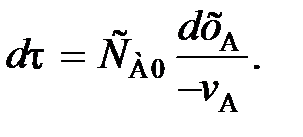 (83)
(83)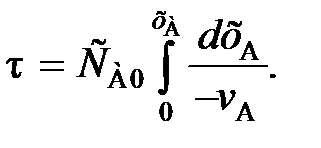 (84)
(84)
 (85)
(85)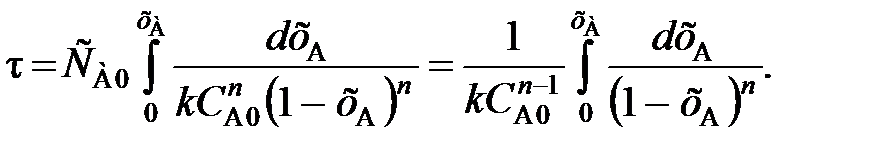 (86)
(86)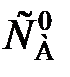 = k. (87)
= k. (87)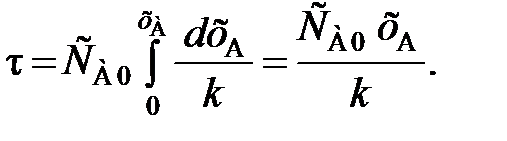 (88)
(88)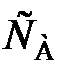 = k
= k 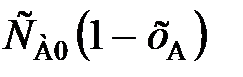 , (89)
, (89)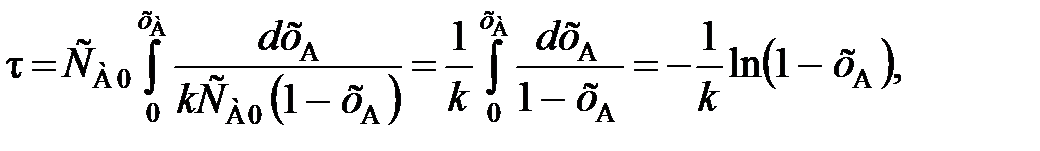 (90)
(90)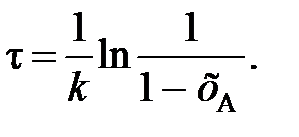 (91)
(91)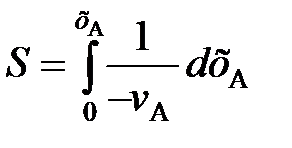 . (92)
. (92)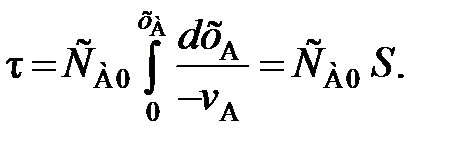 (93)
(93)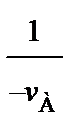
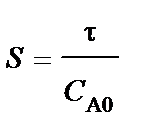
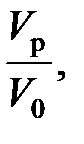 (94)
(94)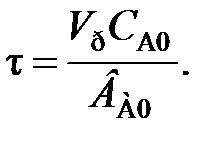 (95)
(95)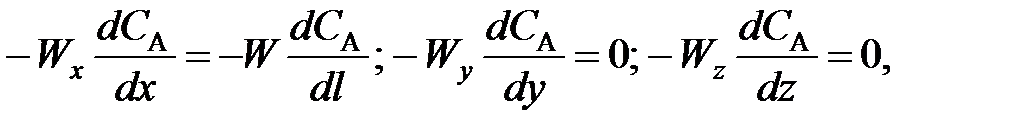 (96)
(96)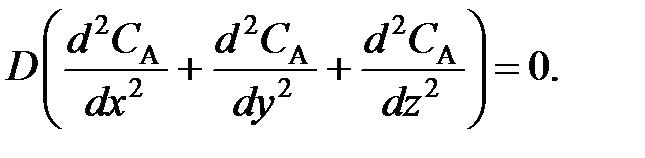 (97)
(97)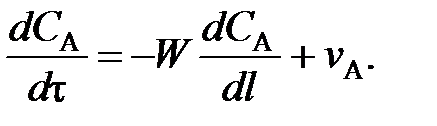 (98)
(98)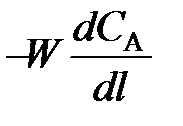 и от расхода вещества на химическую реакцию vА.
и от расхода вещества на химическую реакцию vА. (99)
(99)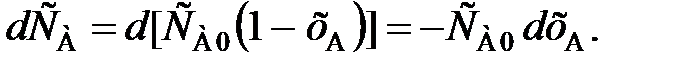 (100)
(100)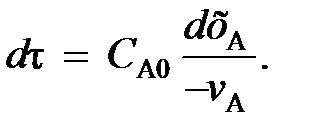 (102)
(102)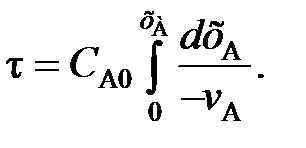 (103)
(103)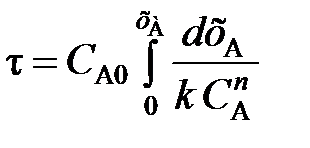 (104)
(104)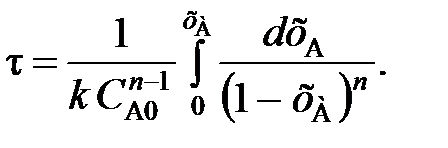 (105)
(105) (106)
(106)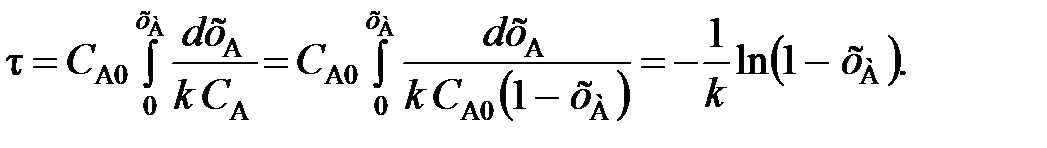 (107)
(107)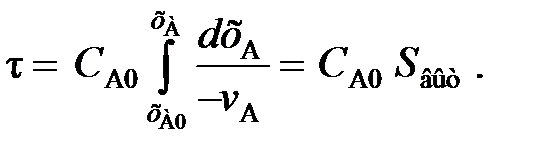 (108)
(108)
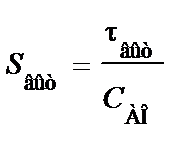
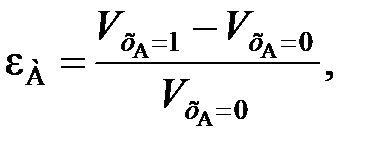 (109)
(109)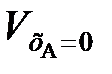 ,
, 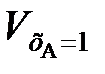 – объемы реакционной смеси соответственно при хА = 0 и хА = 1.
– объемы реакционной смеси соответственно при хА = 0 и хА = 1.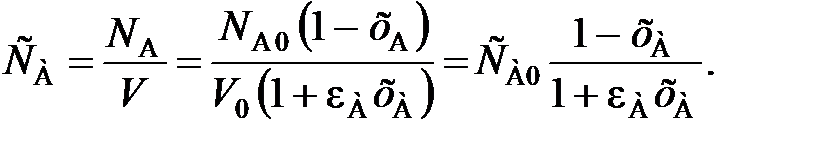 (111)
(111)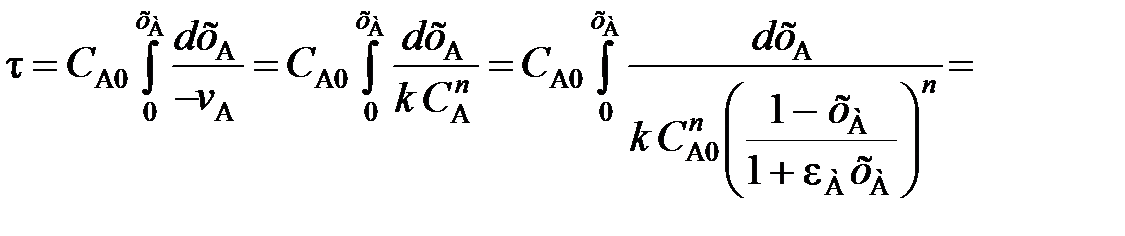
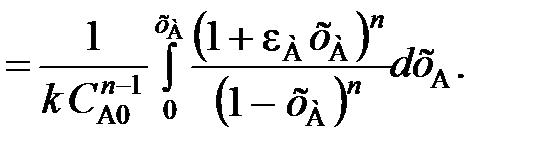 (112)
(112)
















