Нелинейное дифференциальное уравнение второго порядка примеры решений

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Нелинейное дифференциальное уравнение второго порядка примеры решений

Мир математических уравнений

Точные решения > Обыкновенные дифференциальные уравнения > Нелинейные обыкновенные дифференциальные уравнения второго порядка

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

3. Нелинейные обыкновенные дифференциальные уравнения второго порядка

3.1. Дифференциальные уравнения вида y′′ = f(x, y)

1. y′′ = f(y). Автономное уравнение.
2. y′′ = Ax n y m . Уравнение Эмдена—Фаулера.
3. y′′ + f(x)y = ay −3 . Уравнение Ермакова.
4. y′′ = f(ay + bx + c).
5. y′′ = f(y + ax 2 + bx + c).
6. y′′ = x −1 f(yx −1 ). Однородное уравнение.
7. y′′ = x −3 f(yx −1 ).
8. y′′ = x −3/2 f(yx −1/2 ).
9. y′′ = xk−2 f(x −k y). Обобщенно-однородное уравнение.
10. y′′ = yx −2 f(x n y m ). Обобщенно-однородное уравнение.
11. y′′ = y −3 f(y(ax 2 + bx + c) −1/2 ).
12. y′′ = e −ax f(e ax y).
13. y′′ = yf(e ax y m ).
14. y′′ = x −2 f(x n e ay ).
15. y′′ = (ψ′′/ψ)y + ψ −3 f(y/ψ), ψ = ψ(x).

3.2. Дифференциальные уравнения вида f(x, y)y′′ = g(x, y, y′)

1. y′′ − y′ = f(y). Автономное уравнение.
2. y′′ + f(y)y′ + g(y) = 0. Уравнение Льенарда.
3. y′′ + [ay + f(x)]y′ + f′(x)y = 0.
4. y′′ + [2ay + f(x)]y′ + af(x)y 2 = g(x).
5. y′′ = ay′ + e 2axf(y).
6. y′′ = f(y)y′.
7. y′′ = [e αxf(y) + α]y′.
8. xy′′ = ny′ + x 2n + 1 f(y).
9. xy′′ = f(y)y′.
10. xy′′ = [x k f(y) + k − 1]y′.
11. x 2 y′′ + xy′ = f(y).
12. (ax 2 + b)y′′ + axy′ + f(y) = 0.
13. y′′ = f(y)y′ + g(x).
14. xy′′ + (n + 1)y′ = xn − 1 f(yx n ).
15. g(x)y′′ + 1/2 g′(x)y′ = f(y).
16. y′′ = −ay′ + e ax f(ye ax ).
17. xy′′ = f(x n e ay )y′.
18. x 2 y′′ + xy′ = f(x n e ay ).
19. yy′′ + (y′) 2 + f(x)yy′ + g(x) = 0.
20. yy′′ − (y′) 2 + f(x)yy′ + g(x)y 2 = 0.
21. yy′′ − n(y′) 2 + f(x)y 2 + ay 4n − 2 = 0.
22. yy′′ − n(y′) 2 + f(x)y 2 + g(x)yn + 1 = 0.
23. yy′′ + a(y′) 2 + f(x)yy′ + g(x)y 2 = 0.
24. yy′′ = f(x)(y′) 2 .
25. y′′ − a(y′) 2 + f(x)e ay + g(x) = 0.
26. y′′ − a(y′) 2 + be 4ay + f(x) = 0.
27. y′′ + a(y′) 2 − 1/2 y′ = e x f(y).
28. y′′ + α(y′) 2 = [e βxf(y) + β]y′.
29. y′′ + f(y)(y′) 2 + g(y) = 0.
30. y′′ + f(y)(y′) 2 − 1/2 y′ = e x g(y).
31. y′′ = xf(y)(y′) 3 .
32. y′′ = f(y)(y′) 2 + g(x)y′.
33. y′′ = f(x)g(xy′ − y).
34. y′′ = yx −2 f(xy′/y).
35. gy′′ + 1/2 g′y′ = f(y)h(y′g 1/2 ), g = g(x).
36. y′′ = f((y′) 2 + ay).

Веб-сайт EqWorld содержит обширную информацию о решениях различных классов обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, интегральных уравнений, функциональных уравнений и других математических уравнений.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

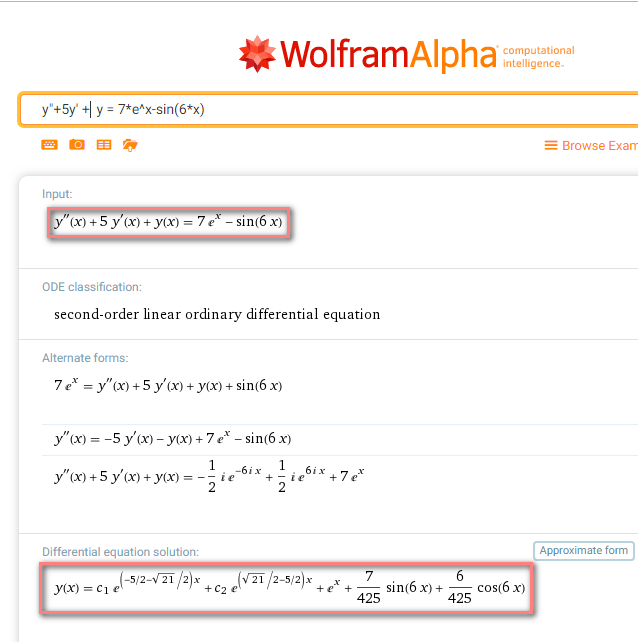
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Мгновенный глубокий сон с мягким дождем на дорожке ночью😴Расслабляющие звуки дождя для сна и стрессаСкачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:Дифференциал функцииСкачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Примеры решений дифференциальных уравнений второго порядка методом Лагранжа

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Видео:Как распознать талантливого математикаСкачать

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

📽️ Видео

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

17. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Ч2Скачать