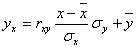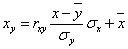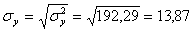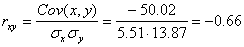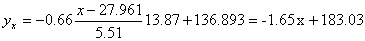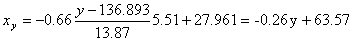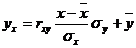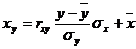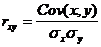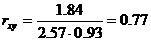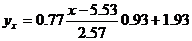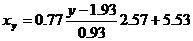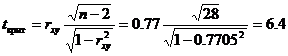Видео:Парная регрессия: линейная зависимостьСкачать
Корреляционная таблица
Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и 
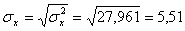
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Видео:Математика #1 | Корреляция и регрессияСкачать
Задача по эконометрике 3
Задача 3. Определить выборочное уравнение прямой линии регрессии Y на Х по данным корреляционной таблицы. Найти интервал для истинного значения коэффициента корреляции.
Так как данные наблюдений между признаками Х и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то для упрощения вычислений можем перейти к условным вариантам:
,
,
где С1, С2 – «ложные нули» вариант Х и Y соответственно (новые начала отсчета); h1, h2 – шаги (разности между двумя соседними вариантами).
С1=40; h1=10; 
С2=15; h2=5;
Итого
5
10
54
17
14
Итого nu
2
10
6
64
15
3
100
Вычислим групповые средние ūi и νi
Определяем теперь χ и ȳ по формулам:
Вычислим коэффициент корреляции.
При переходе к условным вариантам коэффициент корреляции вычисляется по формуле:
Так как коэффициент корреляции положителен, то делаем вывод о положительной связи между рассматриваемыми признаками, т.е. с увеличением значений признака Х значения признака Y тоже растут.
Найдем уравнение прямой регрессии Y на Х по формуле:
— искомое выборочное уравнение прямой линии регрессии Y на Х
Найдем доверительный интервал для коэффициента корреляции при доверительной вероятности 0,95 по формуле:
Для k=n-2=100-2=98 t=tтабл=1,984
С вероятностью 0,95 истинное значение коэффициента корреляции лежит в пределах от 0,566 до 0,734.
Видео:Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать
Найти выборочное уравнение прямой линии регрессии Y на Х по данным
- Реферат.Справочник
- Решенные задачи по высшей математике
- Найти выборочное уравнение прямой линии регрессии Y на Х по данным
Условие
Найти выборочное уравнение прямой линии регрессии Y на Х по данным, привеенным в корреляционной таблице. X Y 10 15 20 25 30 35 20 1 5 7 4 40 2 4 6 5 60 3 5 4 6 80 10 2 3 5 100 2 4 4 8 10
Решение
Составим дополнительную таблицу.
Х
10 15 20 25 30 35
Y 20 1 5
7
4 17
40 2
4
6 5 17
60
3 5 4 6
18
80 10
2 3
5 20
100 2 4
4 8 10 28
15 12 11 18 20 24 100
Уравнение линейной регрессии по : .
Коэффициент корреляции: .
Математические ожидания найдем по формулам:
и
Дисперсии найдем по формулам:
и
Ковариацию найдем по формуле:
Промежуточные вычисления сделаем в таблице:
10 20 15 17 150 340 1500 6800
15 40 12 17 180 680 2700 27200
20 60 11 18 220 1080 4400 64800
25 80 18 20 450 1600 11250 128000
30 100 20 28 600 2800 18000 280000
35
24
840
29400
Сумма 100 100 2440 6500 67250 506800
Математические ожидания:
и
Дисперсии:
и
Ковариация равна:
Коэффициент корреляции:
Уравнение линейной регрессии по : .
📺 Видео
Линейная регрессияСкачать
Эконометрика. Линейная парная регрессияСкачать
Метод наименьших квадратов. Линейная аппроксимацияСкачать
Линейная регрессияСкачать
Эконометрика Линейная регрессия и корреляцияСкачать
Составляем уравнение прямой по точкамСкачать
Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать
9 класс, 7 урок, Уравнение прямойСкачать
Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Уравнение прямой по графику. ПримерыСкачать
Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать
Метод наименьших квадратов. Регрессионный анализ.Скачать
Расчет коэффициента корреляции в ExcelСкачать
Построение уравнения линейной регрессии методом наименьших квадратов.Скачать
Линейная регрессия. Постановка задачиСкачать
Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать
