Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Результат
Примеры комплексных выражений
- Деление комплексных чисел
- Умножение комплексных чисел
- Комплексные уравнения
- Возведение комплексного числа в степень
- Корень из комплексного числа
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Найти корень из комплексного числа онлайн, подробное решение
Онлайн калькулятор предназначен для вычисления корня -ой степени из комплексного числа, с описанием подробного хода решения на русском языке. Для нахождения корня -ой степени, сначала необходимо выбрать (алгебраическую, тригонометрческую или показательную) форму представления комплексного числа. Далее приведены минимальные теоретические сведения, необходимые для понимания решения, выдаваемого калькулятором.
Согласно теории, корень -ой степени из любого числа ( ) имеет ровно значений. Например:
Пример, по интереснее:
где — мнимая единица. Можете попробовать возвести все значения в куб, и действительно получите . Возникает вопрос: как найти все значений корня -ой степени из числа? Для этого необходимо использовать формулу Муавра, причем комплексное число должно быть записано в тригонометрической форме. Наш калькулятор автоматически осуществит перевод введенного числа в тригонометрическую форму, если потребуется.
Видео:Решение, дано комплексное число z=−1+√3i. Найти корни уравнения ω3+z=0, пример 2Скачать
Решение уравнений с комплексными числами
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:
где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:
Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
Найдем корни уравнения:
Ответ:
Пример 3. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
Пример 4. Найти корни уравнения
Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
🎬 Видео
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
Комплексные корни квадратного уравненияСкачать
АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать
Решение, дано комплексное число z=−2+2√3i. Найти корни уравнения ω3+z=0, пример 4 Высшая математикаСкачать
Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать
Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать
Откуда три корня? ➜ Решите уравнение z³=1Скачать
Как решают уравнения в России и СШАСкачать
🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать
КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать
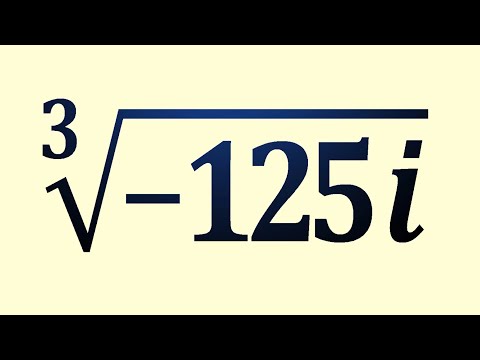
Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать
Как считать корни? #shortsСкачать
СЛОЖИТЕ ДВА КОРНЯСкачать
Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать
Математика Один из корней уравнения 3x^2 +5x +2m =0 равен -1. Найдите второй корень.Скачать
