Условие
Дано комплексное число a . Требуется: 1) записать
число a в алгебраической и тригонометрической формах; 2) найти все корни
уравнения z^(3) + a= 0 и изобразить их на комплексной плоскости
a=(2sqrt(2))/(1-i)
Решение
Умножаем и числитель и знаменатель на[m] (1+i)[/m]
[m]a=2cdot (cosfrac+icdot sin frac)[/m] — тригонометрическая форма
Извлекаем кубический корень из числа (-а).
Для этого применяем формулу Муавра.
Представляем число ( -a) в тригонометрической форме:
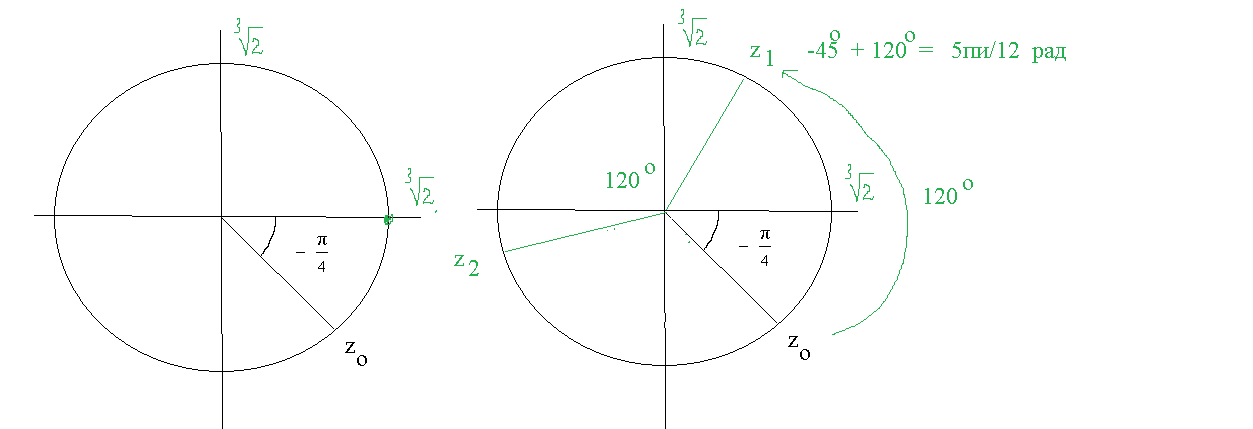
Эта точка находится на окружности радиуса [m] r=sqrt[3] [/m] на луче (-π/4)
Эта точка находится на окружности радиуса [m] r=sqrt[3] [/m] на луче (-π/4)+(2π/3)=5π/12
Эта точка находится на окружности радиуса [m] r=sqrt[3] [/m] на луче (5π/12)+(2π/3)=13π/12
Три точки делят окружность 360 ° на [b]три[/b] равные части ( потому что корень третьей степени)
по 120 ° между ними . 
Видео:Комплексные корни квадратного уравненияСкачать
Найти все корни уравнения 3 2 2z a и изобразить их на комплексной плоскости
. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке
© Контрольная работа РУ — примеры решения задач
Видео:Изобразить область на комплексной плоскостиСкачать
Комплексные числа по-шагам
Видео:Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
Результат
Примеры комплексных выражений
- Деление комплексных чисел
- Умножение комплексных чисел
- Комплексные уравнения
- Возведение комплексного числа в степень
- Корень из комплексного числа
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
🔥 Видео
Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать
Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать
Извлечение корня из комплексного числаСкачать
ТФКП. Как найти все значения корня из комплексного числаСкачать
Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать
Решение, найти и изобразить на комплексной плоскости корни уравнения z^2+9=0. пример 12Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Тригонометрическая форма комплексного числаСкачать
Число корней уравнения в кольце. Теорема РушеСкачать
Биквадратное уравнение. Комплексные корни.Скачать
Возведение в степень и извлечение корня из комплексного числаСкачать
10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать
11 класс, 10 урок, Извлечение корней из комплексных чиселСкачать
Комплексные корни квадратных уравнений. 11 класс.Скачать
10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать
Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать
