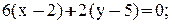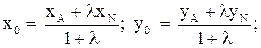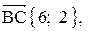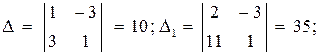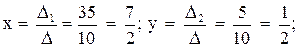Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Уравнение высоты треугольника по координатам формула
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Даны координаты вершин треугольника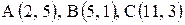 
.
1) Вычислить длину стороны 
.
2) Составить уравнение линии .
3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.
4) Найти точку пересечения медиан.
5) Найти косинус внутреннего угла при вершине В.
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.
А
1. Длина стороны ВС равна модулю вектора 
.
; 
.
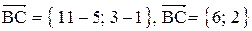
2. Уравнение прямой ВС: 
; 
; 
.
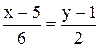
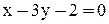
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку 
перпендикулярно вектору 
: 
. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: 
.
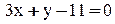
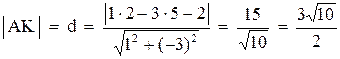
4. Найдем координаты точки N – середины стороны ВС:
; 
; 
.
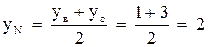
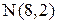
Точка пересечения медиан О делит каждую медиану на отрезки в отношении 
.
Используем формулы деления отрезка в данном отношении 
:
.
5. Косинус угла при вершине В найдем как косинус угла между векторами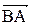 
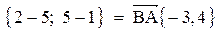
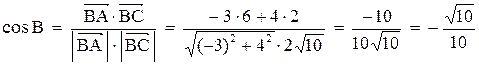
и 
; 
.
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы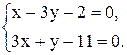 
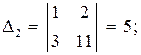
Систему решим по формулам Крамера: 
.
Точка К является серединой отрезка АМ.
.
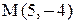
Контрольные варианты к задаче 2
Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение линии ВС;
3) составить уравнение высоты, проведенной из вершины А;
4) вычислить длину высоты, проведенной из вершины А;
5) найти точку пересечения медиан;
6) вычислить внутренний угол при вершине В;
7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
| 1. | 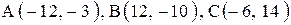 . | 2. |  . |
| 3. |  . | 4. |  . |
| 5. |  . | 6. |  . |
| 7. |  . | 8. |  . |
| 9. | 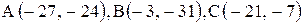 . | 10. |  . |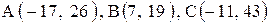
| 11. | 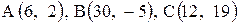 . | 12. |  . |
| 13. |  . | 14. |  . |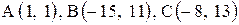
| 15. | 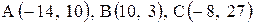 . | 16. |  . |
| 17. | 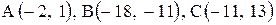 . | 18. |  . |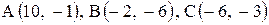
| 19. | 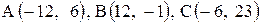 . | 20. |  . |
| 21. | 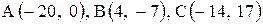 . | 22. |  . |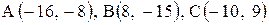
| 23. | 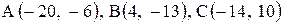 . | 24. |  . |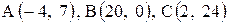
| 25. |  . | 26. |  . |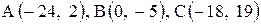
| 27. | 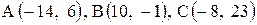 . | 28. |  . |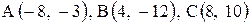
| 29. | 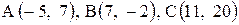 . | 30. |  . |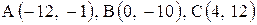
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10637 – 
| 8008 – 
или читать все.
| ЛУЧШИЙ ОТВЕТ |
Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @
Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)
Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:
Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0
Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9
Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:
y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.
10 = (32/3) + d,
d = -2/3
Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0
Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: XE = 6, YE = -1
Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.
(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0
Это уравнение медианы AE.
Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:
S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)
Видео:Вычисляем высоту через координаты вершин 1Скачать
Найти уравнение высоты ad опущенной из вершины a на сторону bc
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
🎦 Видео
Уравнения стороны треугольника и медианыСкачать
Математика без Ху!ни. Смешанное произведение векторовСкачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
найти уравнение высоты треугольникаСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Задача 6 №27611 ЕГЭ по математике. Урок 61Скачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
№496. Основание D высоты CD треугольника ABC лежит на стороне АВ, причем AD=BC.Скачать
Задача 6 №27436 ЕГЭ по математике. Урок 50Скачать
Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать
Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать
Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать
Разбор Задачи №16 из Варианта Ларина №285Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
