Найти уравнение траектории движения частицы

Видео:Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

• прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
• и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение траектории движения

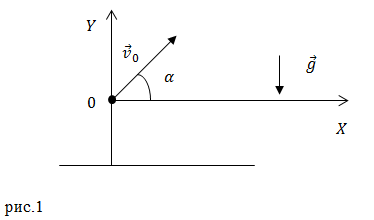
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

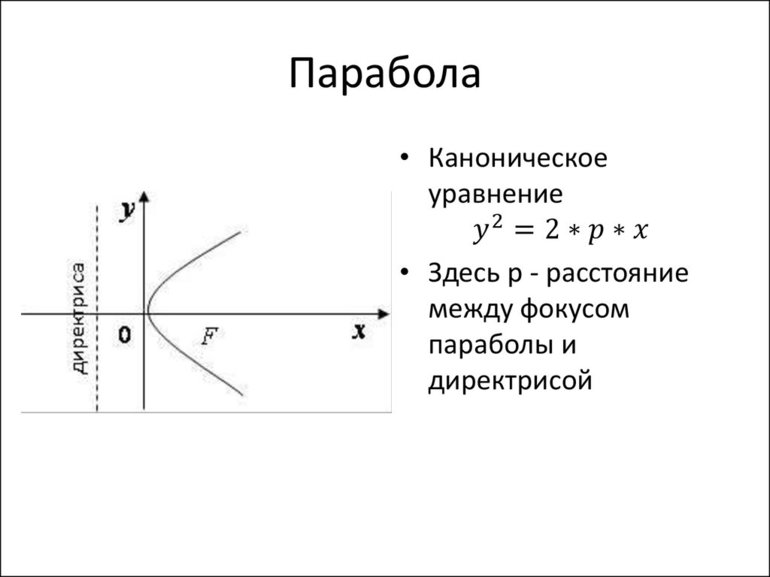
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Видео:Кинематика точки Задание К1Скачать

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

• Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
• При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
• Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Видео:Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

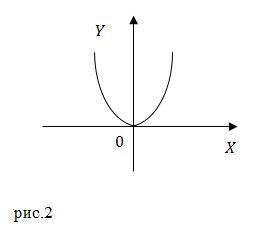
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Движение частицы в центральном поле

12.1. Сохранение момента импульса в центральном поле.

Сила называется центральной, если для всех точек поля она направлена к одной и той же точке (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил, или силовым центром.

Уже из определения следует, что центральные силы консервативны.

Итак, центральная сила:

. (12.1)

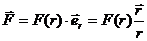
Поскольку эта сила консервативна, то можно ввести потенциальную энергию:

(12.2)

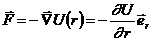
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:

. (12.3)

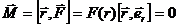
Тогда из уравнения моментов (11.5) получаем, что момент импульса есть постоянная величина.

При движении частицы в центральном поле полный момент импульса сохраняется, несмотря на то, что система (одна частица) не является замкнутой.

. (12.4)

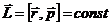
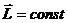
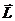
Так как , т.е. величина и направление вектора

сохраняются, а вектор момента импульса всегда

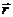
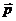
перпендикулярен к векторам и , то движение частицы

происходит в плоскости, перпендикулярной к 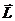. Отсюда следует,

что частица в поле центральных сил движется по плоской орбите.

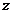
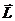
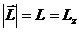
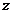
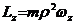
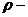
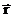
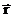
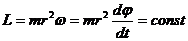
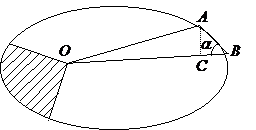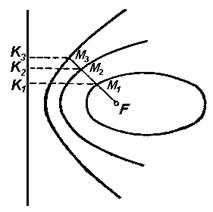
Если ось направлена по вектору , то , а траектория частицы лежит в плоскости, перпендикулярной оси . Выше мы получили, что , где проекция радиус-вектора на плоскость, в которой лежит траектория частицы. В нашем случае, начало координат и вектор лежит в плоскости орбиты, поэтому

. (12.5)

Пусть частица движется в в поле центральных сил по плоской траектории, представляющей собой замкнутую кривую.

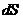
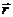
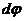
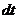
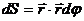
Площадь элементарного сектора, описываемая радиус-вектором при повороте на за время :

.

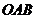
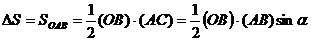
Выберем за начало отсчета точку О и найдем площадь сектора , показанного на рисунке.

.

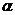
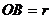
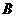
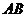
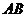
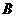
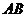
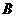
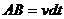
Здесь — угол между (длина радиус-вектора, проведенного к точке ) и . Будем сжимать отрезок к точке . В пределе – касательная к траектории частицы в точке , т.е. .

Тогда можем записать

. (12.6)

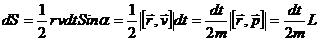
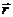
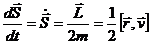
Вводя понятие секториальной скорости как площади, описываемой радиусом-вектором в единицу времени, получаем

. (12.7)

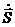
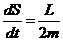
Т.о., мы получили математическое выражение 2-го закона Кеплера, устанавливающего постоянство секториальной скорости планеты при движении в центральном поле:

. (12.8)

Этому закону подчиняется, например, движение планет по эллиптическим орбитам.

Примечание: Закон сохранения момента импульса частицы, движущейся в центральном поле иногда

называют “интегралом площадей”.

Итак, свойства движения частицы в центральном поле:

1) движение плоское, плоскость проходит через точку 0, определенный относительно которой момент импульса частицы сохраняется.

2) секториальная скорость постоянна (II закон Кеплера).

12.2. Закон сохранения энергии в центральном поле.

Центральные силы консервативны, следовательно, полная энергия частицы в системе «силовой центр – частица» (замкнутая система) сохраняется.

. (12.9)

Поскольку задача плоская, удобно воспользоваться полярными координатами и представить импульс частицы в виде суммы радиальной и азимутальной составляющих:

.

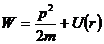
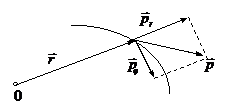
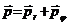
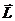
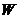
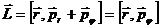
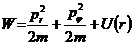
В полярных координатах выражения для момента импульса и полной энергии частицы приобретают вид:

; (12.10)

. (12.11)

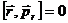
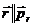
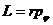
В выражении (12.10) , т.к. , и

, (12.10а)

т.к. траектория частицы плоская и .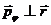

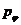
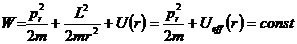
Если, воспользовавшись (12.10), исключить из уравнения (12.11) азимутальную составляющую импульса частицы , то полную механическую энергию частицы можно записать как

. (12.12)

Примечание. Величину 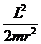называют центробежной энергией.

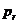
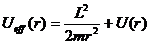
Уравнение (12.12) содержит только одну неизвестную – радиальную компоненту импульса . Поэтому оно может формально рассматриваться как уравнение для энергии одномерного – радиального – движения частицы. В этом случае роль потенциальной энергии играет функция

. (12.13)

Т.о., можно сказать, что задача о движении частицы в центральном поле сводится к нахождению условий финитности (инфинитности) одномерного движения частицы в радиальном направлении в поле, описываемом эффективной потенциальной функцией .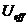

12.3. О траектории движения частицы.

Представим компоненты импульса, записанного в полярных координатах, следующим образом:

(12.14)

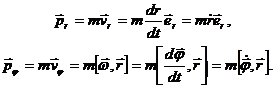
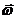
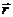
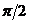
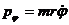
Далее, т.к. угол между вектором угловой скорости и радиус-вектором равен , то

.

Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем

. (12.15)

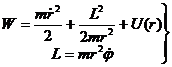
Из второго уравнения (12.15) получаем

.

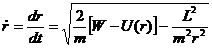
Разделяя переменные, находим в неявном виде зависимость :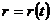

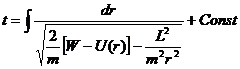
. (12.16)

Из первого уравнения (12.15) имеем

.

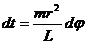
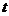
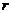
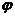
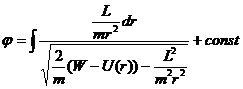
Исключив из уравнений (12.15) время , находим уравнение траектории частицы в центральном поле в полярных координатах (связь между и ):

. (12.17)

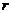
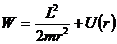
Значения , при которых энергия частицы равна

, (12.18)

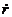
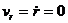
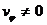
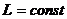
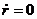
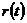
определяют границы области движения по расстоянию от центра поля. При выполнении равенства (12.18) радиальная скорость обращается в нуль. Однако равенство нулю ( ) радиальной составляющей скорости не означает, что частица остановилась, т.к. азимутальная (угловая) компонента скорости отлична от нуля ( ), поскольку в центральном поле . Равенство определяет “точку поворота” траектории, в которой функция достигает либо максимального, либо минимального значения, после чего начинает, соответственно, убывать или возрастать.

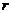
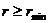
Если область допустимого изменения ограничена лишь условием , то движение частицы инфинитно – её траектория приходит из бесконечности и уходит на бесконечность.

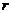
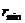
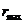
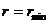
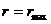
Если область изменения имеет две границы и , то движение является финитным и траектория частицы лежит внутри кольца, ограниченного окружностями и , определяющими границы движения. Однако траектория при этом может оставаться незамкнутой.

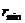
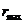
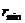
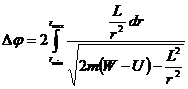
За время прохождения одной петли (от до и снова до ) радиус-вектор частицы совершит поворот на угол

. (12.19)

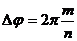
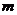
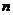
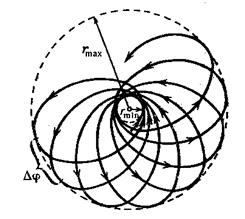
Условие замкнутости траектории: траектория будет замкнутой, если , где и — целые

числа, т.е. за одну петлю радиус-вектор должен повернуться

на угол, равный рациональной части от .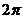

Тогда через 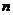повторений этого периода времени радиус-

вектор точки, сделав 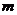полных оборотов, совпадет со своим

первоначальным значением, т.е. траектория замкнется.

Однако такой исход является скорее исключением,

нежели правилом. Существуют лишь два типа центральных

полей, в которых все траектории финитных движений

замкнуты. Это поля, где зависимость потенциальной энергии

от расстояния от центра поля имеет вид:

.

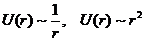
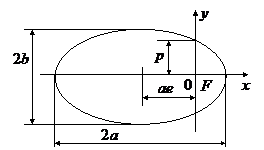
Задача Кеплера (Кеплерова задача) — задача о движении частицы в поле центральных сил, убывающих обратно пропорционально квадрату расстояния от центра поля. Этому закону подчиняются силы гравитационного притяжения между точечными массами (или телами, обладающими сферической симметрией), а также кулоновские силы, действующие между точечными электрическими зарядами. Поэтому такие поля являются важнейшим случаем центральных полей.

В таком поле потенциальная энергия частицы определяется выражением

, (13.1)

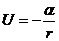
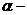
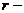
где постоянная величина, расстояние от центра поля.

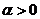
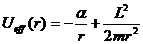
Рассмотрим случай, когда , т.е. сила, действующая на частицу массой, направлена к центру поля и

является силой притяжения. Зависимость эффективной

(13.2)

от расстояния от центра поля показана на рисунке.

При стремится к , а при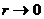

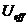
она стремится к нулю со стороны отрицательных

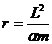
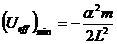
значений; при функция имеет минимум,

. (13.3)

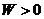
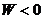
Из рисунка видно, что движение частицы будет инфинитным при , и финитным при .

Форму траектории получаем интегрированием формулы (12.15) после подстановки :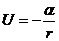

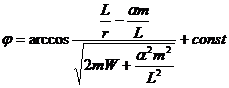
. (13.4)

Выбирая начало отсчета угла так, чтобы постоянная интегрирования обращалась в нуль ( ), и введя обозначения

, , (13.5)

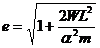
получим уравнение траектории в виде:

. (13.6)

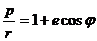
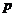
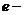
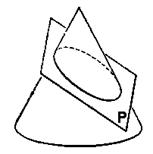
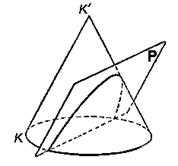
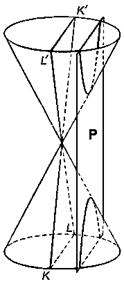
Приложение. Выражение (13.6) – уравнение конического сечения с фокусом в начале координат в полярных координатах; и так называемые параметр и эксцентриситет орбиты, соответственно.

Коническими сечениями называют эллипс, параболу и гиперболу, т.к. их можно получить на поверхности

круглого конуса в пересечении с плоскостью 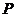, не проходящей через

вершину конуса. При этом поверхность конуса предполагается

неограниченно продолженной в обе стороны от вершины.

Если плоскость 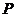не параллельна ни одной образующей конуса, то

коническое сечение есть эллипс. Эллипсом называется геометрическое

место точек, сумма расстояний от которых до двух данных точек,

называемых его фокусами, есть величина постоянная. Отношение

фокусного расстояния эллипса к длине его большой оси называется

эксцентриситетом эллипса .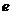

Если плоскость 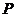параллельна только одной из образующих конуса

( ), то коническое сечение есть парабола. Параболой

называют геометрическое место точек, равноотстоящих

от данной точки, называемой фокусом, и данной прямой

называемой директрисой. Исходя из её определения,

эксцентриситет параболы принимают равным единице

( ).

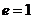
Если плоскость параллельна двум образующим конуса

( и ), то коническое сечение есть гипербола.

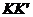
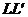
Гиперболой называется геометрическое место точек, разность

расстояний от которых до двух данных точек, называемых

фокусами, есть величина постоянная. Величина, определяемая

как отношение фокусного расстояния к длине действительной

оси (длина отрезка, соединяющего вершины гиперболы), называется

эксцентриситетом гиперболы .

Из аналитической геометрии известно, что все эллипсы (кроме

окружности), параболы и гиперболы обладают следующим свойством: для

каждой из этих линий остается неизменным отношение

,

где расстояние от

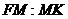
произвольной её точки до

данной точки (фокуса), а

расстояние от точки

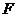
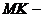
до данной прямой

Обобщая сказанное, можно дать

общее определение конического

сечения (эллипса, гиперболы и

параболы): коническое сечение есть

геометрическое место точек, отношение

расстояний которых до данной точки

(фокуса) и до данной прямой (директрисы) есть величина постоянная .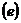

для эллипса ;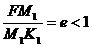

для параболы ;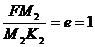

для гиперболы .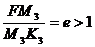

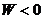
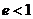
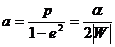
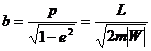
Из (13.5) следует, что при эксцентриситет , т.е. орбита является эллипсом и движение частицы финитно. Большая и малая полуоси эллипса, согласно формулам аналитической геометрии, равны

, (13.7)

. (13.8)

расстояние между фокусами эллипса.

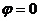
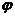
Из уравнения (13.6) следует, что точка с является ближайщей к центру (перигелий орбиты), что, вообще говоря, является следствием сделанного выбора начала отсчета угла .

Наименьшее и наибольшее расстояния частицы от центра поля (фокуса эллипса) составляют (из 13.6)

; (13.9)

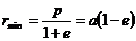
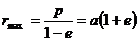
и зависят только от энергии частицы, поскольку из (13.7),

следует, что большая полуось эллипса 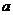зависит только от

энергии, но не от момента импульса частицы).

Примечание. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце –

первый закон Кеплера.

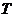
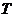
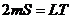
Время обращения по эллиптической орбите (период ) можно определить с помощью закона сохранения импульса частицы в форме “интеграла площадей”. Интегрируя выражение (12.8) по времени от нуля до , получаем

, (13.10)

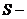
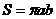
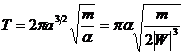
где площадь орбиты. Для эллипса , и используя (13.7) и (13.8), находим

. (13.11)

Тот факт, что квадрат периода обращения должен быть пропорционален кубу линейных размеров орбиты, составляет содержание третьего закона Кеплера.

Отметим, что период обращения, как следует из (13.11) зависит только от энергии частицы.

При 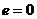, когда энергия частицы достигает минимума (13.3), эллипс вырождается в окружность.

В случае если энергия частицы 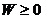, её движение инфинитно.

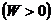
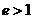
Если энергия частицы положительна , то эксцентриситет её орбиты (см. 13.5), т.е. траектория движения является гиперболой, огибающей фокус (центр поля). Расстояние перигелия от центра

поля определяется выражением

, (13.12)

(13.13)

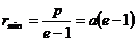
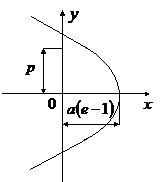
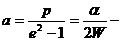
В случае, когда полная энергия частицы

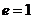
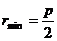
эксцентриситет кривой , т.е. частица движется по параболе,

. (13.14)

Этот случай реализуется, если частица начинает свое движение

из состояния покоя на бесконечности.

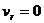
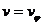
Используя выражение (13.9, 13.12 и 13.14) и соответствующие значения эксцентриситета, можно найти скорость частицы в перигелии при движении по всем рассмотренным траекториям. В точке поворота (перигелии) , поэтому .

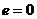
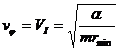
По окружности ( ) будет двигаться частица, имеющая скорость

,

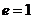
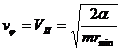
движению по параболе ( ) будет соответствовать скорость

.

Если скорость частицы лежит в интервале

,

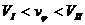
то её траекторией является эллипс ( ).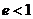

,

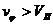
то траектория частицы имеет форму гиперболы ( ).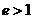

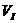
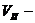
В небесной механике и первая и вторая космические скорости.

Обратимся теперь к движению в поле отталкивания, в котором потенциальная энергия частицы определяется выражением

, (13.15)

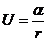
где .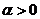

В этом случае эффективная потенциальная энергия частицы

(13.16)

монотонно убывает от бесконечности до нуля

при изменении расстояния от центра поля от нуля до

бесконечности 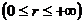. Очевидно, что полная

энергия частицы 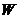может быть только положительной

и её движение инфинитно. Все вычисления в этом случае

полностью аналогичны приведенным выше.

Траектория частицы является гиперболой

, (13.17)

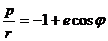
где характеристики кривой по-прежнему определяются

Двигаясь по такой траектории, частица проходит мимо центра поля, как показано на рисунке. Расстояние

. (13.18)

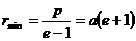
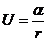
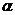
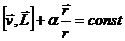
В заключение рассмотрения задачи Кеплера укажем, что при движении в поле центральных сил, котором потенциальная энергия частицы определяется выражением с любым знаком , существует интеграл движения (сохраняющийся во времени вектор), специфический именно для этого поля:

, (13.19)

что легко проверить непосредственным вычислением, взяв от него производную по времени.

Сохраняющийся вектор (13.19) направлен вдоль большой оси от фокуса к перигелию и равен по величине 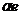. Проще всего в этом убедиться, рассмотрев его значение в перигелии.

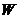
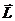
Интеграл движения, наряду с такими сохраняющимися величинами, полная энергия и момент импульса частицы, является однозначной функцией состояния (положения и скорости) частицы.

Видео:Волькенштейн 1.6 * (Сборник задач по физике, 2006)Скачать

Уравнение траектории тела — определение и формулы

Видео:кинематика точкиСкачать

Общие сведения

Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.

В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.

Существует несколько видов механического перемещения (во времени) физической точки:

• равномерное и равноускоренно прямолинейное;
• по дуге;
• гармоническое колебание.

При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.

Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.

Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.

Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.

Видео:ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Горизонтальное перемещение

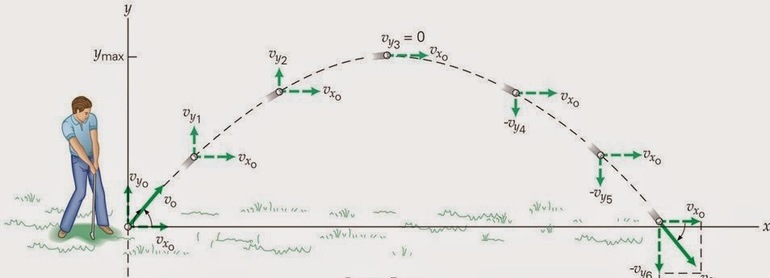
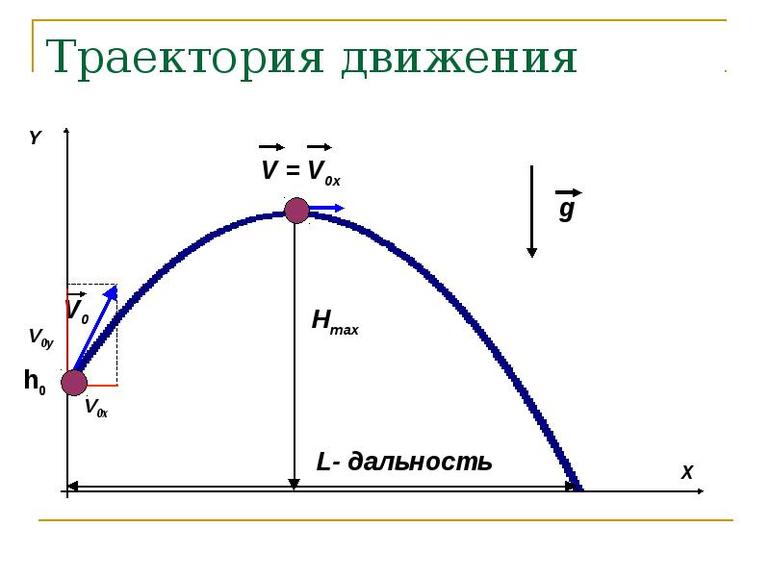
Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).

Таким образом, система начальных условий будет выглядеть так: x (t = 0) = 0; y (t = 0) = 0; v0x = v0; voy = 0. Вектор ускорения постоянный, поэтому a = g. Если тело представить как совокупность материальных точек, движущихся по одинаковому пути, то путь можно определить как сумму перемещений по прямым. Уравнение скорости примет вид: v (t) = v0 + gt. Об изменении положения можно сказать, что оно выполняется с постоянной скоростью и ускорением в горизонтальной плоскости, являясь равномерным. Значит, проекцию на оси ординаты и абсциссы можно записать как vx = v0; vy = -gt.

Скорость перемещения рассчитывают по формуле: V = √‎(V 2 x + V 2 y). После подстановки полученных ранее выражений равенство примет вид: V = √‎(V 2 0 + g 2 t 2 ). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2 ) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.

Так как s0 = y (t = 0) = h0, то скалярные выражения для координат изменяющей положение частицы можно представить в виде системы: x = V0t; y = h0 — (gt 2 / 2). Перемещение происходит по прямой как отдельное движение в двух плоскостях, при этом из формулы следует, что изменение положения будет соответствовать правой половине направленной вниз параболы. Учитывая то, что время можно определить из отношения икса к начальной скорости (t = x /V0), можно записать окончательную формулу для вычисления траектории движения тела: y = h0 — (gx 2 ) / (2 2 V0) .

Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.

Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.

Видео:10.1.04. Уравнение траекторииСкачать

Движение тела под углом

Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.

Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.

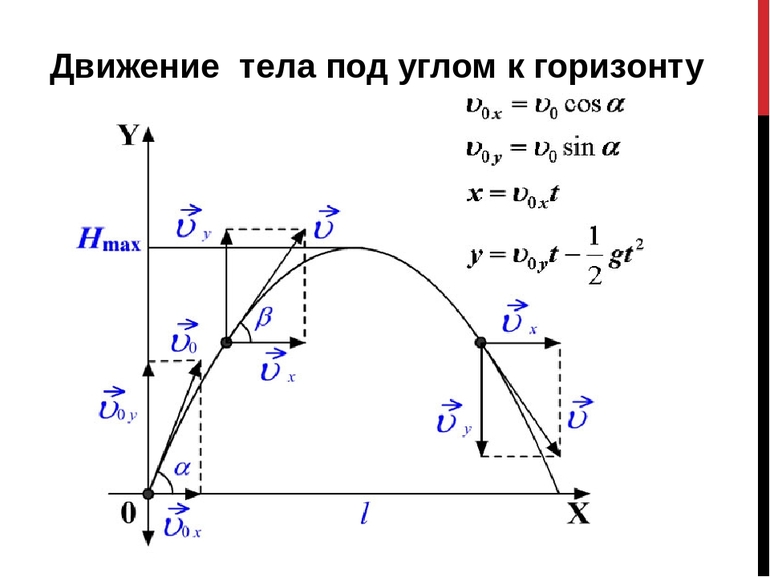
Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:

• ускорения: ax = 0, ay = — g, az = 0;
• радиус-вектора: rx (t) = V0 * cosat, ry (t) = v * sin (at — (g * t2)/2)), rz (t) = 0;
• скорости: vx (t) = V0 * cosa, vy (t) = V0 * sin (a — gt), vz (t) = 0.

Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).

Если полученную формулу для времени подставить в уравнение для игрек координаты, то вместо временного параметра появится икс. То есть можно будет вывести зависимость абсциссы от ординаты: y = V 0 * sinat — (g * t 2 ) / 2 = (tga) * x — (g / 2 * V0 * cos 2 a) * x 2 . Значение t нужно подставить в каждое слагаемое, но при этом учесть, что отношение синуса к косинусу называют тангенсом. Альфа в формуле — это угол между направлением начальной скорости и горизонтальным направлением (угол броска). После исключения времени из этих уравнений получим уравнение траектории.

В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.

Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Решение задач

Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.

Вот два таких задания:

1. Пусть имеется тело, движение которого описывается равенствами: x = Vx * t; y = y0 + Vy * t. Нужно определить траекторию его перемещения, учитывая, что Vx = 20 см/с, Vy = 2 м/с, Yo = 0,2 м. Для решения задачи нужно записать систему, определяемую исходными данными. Затем из первого равенства выразить время: t = x / Vx. Полученную формулу можно подставить в выражение нахождения координат абсциссы: y = y0 + (Vy * x) / Vx. Если теперь использовать исходные данные, то уравнение, описывающее траекторию, примет вид: y = 0.2 + 4x. Равенство напоминает собой формулу прямой: y = k * x + b. Исходя из этого можно утверждать, что траектория пути также будет представлять собой прямую линию. Действительно, в этом можно убедиться, если построить график движения. Для этого нужно взять несколько произвольных значений для икса, подставить их в формулу и найти вторую координату.
2. Следующая задача довольно интересная. Нужно составить траекторию движения для тела, движущегося равномерно со скоростью два метра в секунду, при отклонении пути от оси икс на 60 градусов. За начало координат нужно принять точку (0, 0). Тогда начальный радиус-вектор тоже будет равен нулю: R = 0. Для успешного решения примера понадобится вспомнить скалярные уравнения для проекции при равномерном движении. Так как по условию вектор задан, то можно найти его проекцию на ось игрек: Vx = v * cos60 = 1; Vy = v * cos30 = √‎3. Отсюда: x = Vx * t = t; y = Vy * t = √‎3t.

Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.

Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

🎦 Видео

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Кеплерова задача. Часть 1. Уравнение траекторииСкачать

Кинематика. Закон движения. Урок 3Скачать

Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

Уравнение движенияСкачать

55. Движение частиц в электромагнитных поляхСкачать

Кинематика точки в плоскости. ТермехСкачать

Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Движение в центральном полеСкачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать