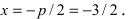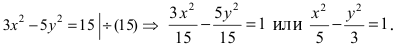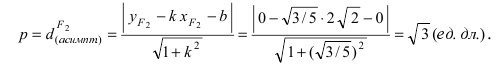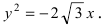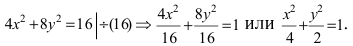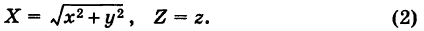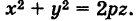Глава VI. Простейшие криволинейные поверхности и тела вращения.
§ 75*. Поверхности вращения
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение
y = f(x), х 
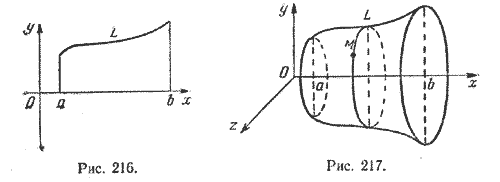
Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).
Очевидно, точка M с координатами (х; у; z), где х 
Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).
Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид
y 2 + z 2 = (f(x)) 2 , х 
Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,
В частности, если кривая L задана уравнением
то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид
т. е. просто y 2 заменяем на y 2 + z 2 .
2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.
Пусть в плоскости хОу эллипс задан уравнением
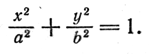
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим
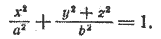
Это уравнение обычно записывают так:
При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:
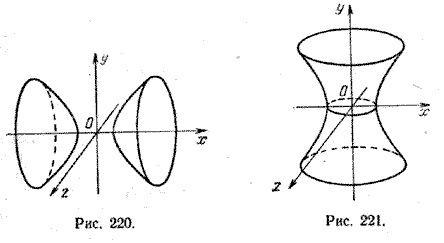
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).
Пусть в плоскости хОу гипербола задана уравнением
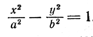
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим
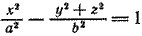
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим
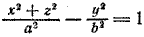
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.
Составим уравнение гиперболы:
Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим
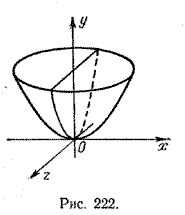
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).
Пусть на плоскости хОу парабола задана уравнением
Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим
Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.
Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).
Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.
Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим
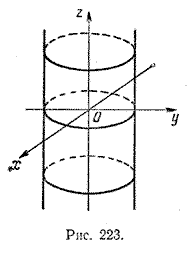
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.
Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение
Эта цилиндрическая поверхность изображена на рис. 223.
Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.
В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.
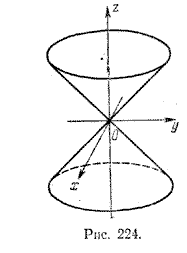
Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид
Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).
Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.
Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.
Видео:560. Уравнение поверхности вращенияСкачать

Парабола — определение и вычисление с примерами решения
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы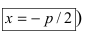
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 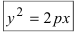
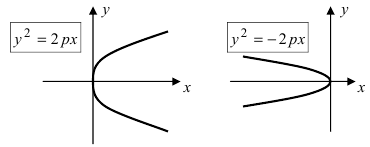
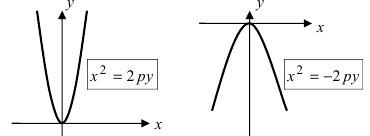
Рис. 35а. Параболы и их уравнения.
Рис. 356. Параболы и их уравнения.
Найдем координаты точек пересечения параболы с координатными осями:
— точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью ординат.
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 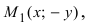
Пример:
Дано уравнение параболы 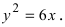
Решение:
Так как из уравнения параболы 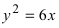
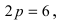
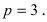
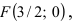
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 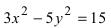
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 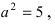
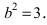
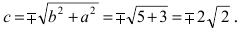
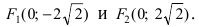
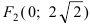
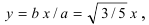
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 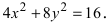
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 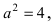
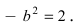
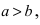
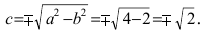
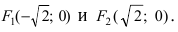
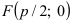
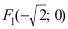
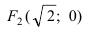

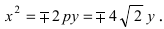
Видео:§64 Поверхности вращенияСкачать

Уравнение параболоида вращения
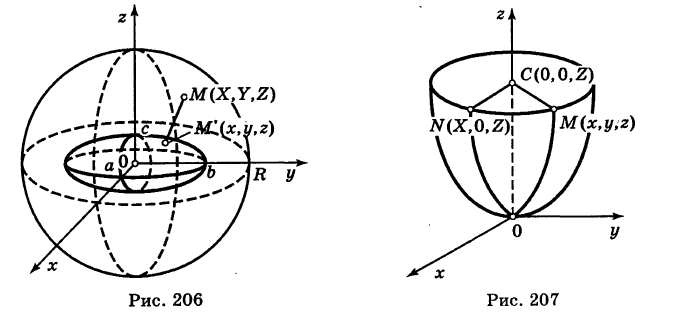
Пусть вертикальная парабола
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 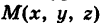
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Поверхности второго порядка. Поверхности вращения.
Поверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M0(x0,y0,z0)
этой поверхности окружность, проходящая через эту точку в плоскости z=z0 с центром в (0,0,z0) и радиусом

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением
F(x 2 +y 2 ,z)=0, то S — поверхность вращения вокруг оси OZ.
Эллипсоид:


Мнимый эллипсоид.
где a > 0, b > 0, c > 0. Эта поверхность не имеет ни одной вещественной точки.
Свойства эллипсоида.
1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что 

2. Эллипсоид обладает:
- центральной симметрией относительно начала координат,
- осевой симметрией относительно координатных осей,
- плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается
Однополостной гиперболоид.
Свойства однополостного гиперболоида.
1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что
2. Однополостной гиперболоид обладает:
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается
эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
 |  |
Двуполостной гиперболоид.
Свойства двуполостного гиперболоида.
1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует,
что 
2. Двуполостный гиперболоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при
получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям
Ox и Oy, – гипербола.
 |  |  |
 |  |
В случае, если a=b≠0, перечисленные выше (эллипсоид, однополостной гиперболоид, двуполостной
гиперболоид, эллиптический параболоид) поверхности являются поверхностями вращения.
Эллиптический параболоид.
Свойства эллиптического параболоида.
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует,
что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает:
- осевой симметрией относительно оси Oz,
- плоскостной симметрией относительно координатных осей Oxz и Oyz.
3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а
плоскостями, ортогональными осям Ox и Oy – парабола.
Уравнение эллиптического параболоида имеет вид:
Если a=b, то эллиптический параболоид представляет собой поверхность вращения, образованную
вращением параболы, параметр которой 
вершину и фокус данной параболы.
Пересечение эллиптического параболоида с плоскостью z=z0>0 является эллипсом.
Пересечение эллиптического параболоида с плоскостью x=x0 или y=y0 является параболой.
🌟 Видео
Поверхности второго порядкаСкачать

Как легко составить уравнение параболы из графикаСкачать

Поверхность вращения.Скачать

§24 Каноническое уравнение параболыСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядка. Поверхности вращенияСкачать
Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Лекция 5. Поверхности вращения. часть 1.Скачать

Площадь поверхности вращенияСкачать

Лекция 16 Поверхности второго порядка. Поверхности вращения. Неполное уравнение поверхностей.Скачать

Лекция 5. Поверхности вращения. Часть 2.Скачать

Площадь эллипсоида + вывод формулы площади поверхности вращенияСкачать

Поверхности вращенияСкачать

Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Лекция 15 Вывод уравнения параболы. Неполное (смещенное) уравнение кривой второго порядка.Скачать

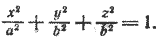
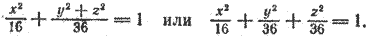
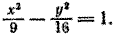
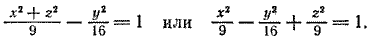
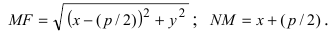
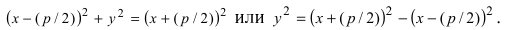
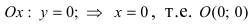 — точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью абсцисс;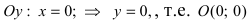 — точка пересечения параболы с осью ординат.
— точка пересечения параболы с осью ординат.