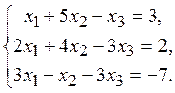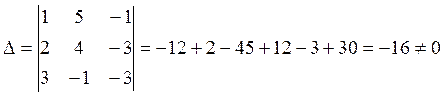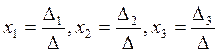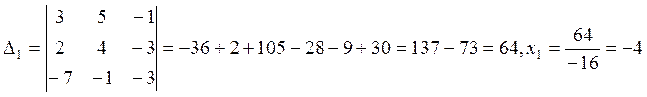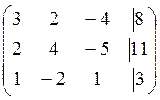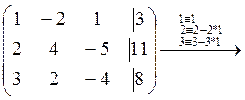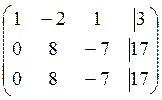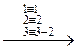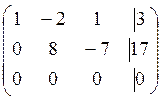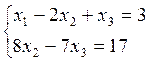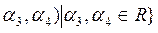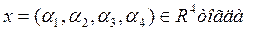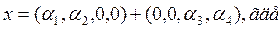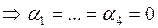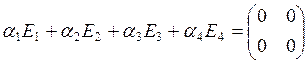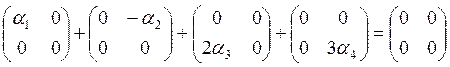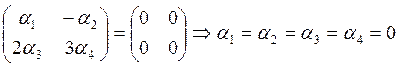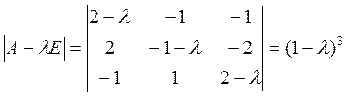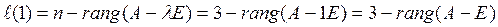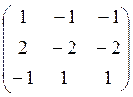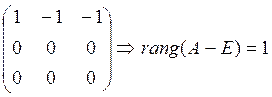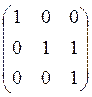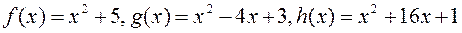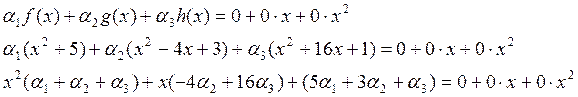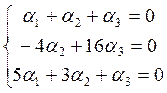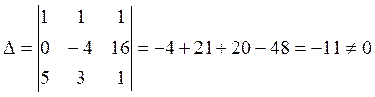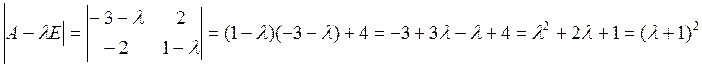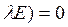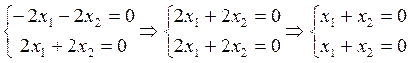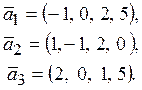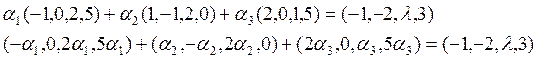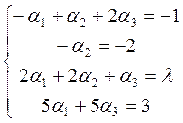Найти систему линейных уравнений подпространство решений которой совпадает с линейной об (6 видео)

Способы описания подпространств линейного пространства

Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.

Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .

Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.

Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .

Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:

1) составить из данных столбцов матрицу размеров ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,

– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.

Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.

Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.

Содержание

Переход от одного способа описания подпространств к другому
23. Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений
Исследование системы на совместимость и решение методом Крамера. Решение системы линейных алгебраических уравнений методом Гаусса
Страницы работы
Содержание работы
📹 Видео

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Переход от одного способа описания подпространств к другому

Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений .

Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.

Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .

Решение. 1. Составляем матрицу и блочную матрицу:

2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):

Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу

3. Из последних строк матрицы составляем матрицу искомой системы.

4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .

Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.

1. Найти фундаментальную систему решений однородной системы . Искомая размерность .

2. Представить заданное пространство как линейную оболочку .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;

– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;

– из последних столбцов матрицы составить фундаментальную матрицу .

Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.

Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.

Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6

Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .

2. Столбцы являются искомым базисом, так как они линейно независимы и .

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

23. Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений

Пусть дано N-Мерное линейное пространство L и пусть в нём зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть М – линейное подпространство в L .

Определение 30. Будем говорить, что Система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов.

Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга R с n Переменными задаёт в любом N-Мерном пространстве Ln (если в нём зафиксирован базис) (N–r )-мерное линейное подпространство.

Справедливо и обратное утверждение. А именно, имеет место следующая теорема.

Теорема 30. Если в линейном N-Мерном пространстве Ln Зафиксирован базис, то любое его К-мерное линейное подпространство можно задать системой линейных однородных уравнений с N Неизвестными ранга (N – к).

Доказательство. Пусть в Ln зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть Lк – линейное К-мерное подпространство в Ln. Выберем в Lк Любой базис А = (А1, а2,… , ак). Пусть В матричной форме А = Е × А, где А = .

Так как А – базис, то ранг матрицы А Равен К.

Получили параметрические уравнения, определяющие Lк .

После исключения параметров получится система (N – к) линейных однородных уравнений. Векторы А1, а2, … , ак являются её линейно независимыми решениями. Все остальные решения являются их линейными комбинациями.

Следовательно, система векторов (А1, а2, … , ак) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (N – к).

Пример. В пространстве L5 зафиксирован базис Е = (Е1, Е2, е3, е4 , Е5 ). Найти систему линейных однородных уравнений, задающих L3 = , если А1 = (1, –2, 2, 0, 1), А2 = (0, 4, 7, 0, 1), А3 = (–2, 3, –1, 0, 0).

Решение. Найдём ранг системы векторов (А1, а2, а3 ). Для этого достаточно найти ранг матрицы . Минор . Окаймляющий минор ¹ 0, следовательно, ранг матрицы равен 3, т. е. векторы А1, а2, а3 линейно независимы и подпространство L3 – трёхмерное. Согласно доказанной теоремы, оно может быть задано системой линейных однородных уравнений ранга 2.

D Î L3 Û D = с1А1 + С2А2 + С3А3 . Отсюда D Î L3 Û Х1 = с1 – 2с3 , х2 = –2с1 + 4с2 + 3с3 , х3 = 2с1 + 7с2 – с3 , х4 = 0, х5 = с1 + с2. Если из первого, второго и пятого уравнений выразить С1, с2 и С3 И подставить их в третье и четвёртое уравнения, то получим следующую систему

Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.

Видео:Исследование систем линейных уравнений на совместностьСкачать

Исследование системы на совместимость и решение методом Крамера. Решение системы линейных алгебраических уравнений методом Гаусса

Страницы работы

Содержание работы

1. Исследовать систему на совместимость и решить методом Крамера.

Т-ма Крамера: крамеровская система имеет единственное решение.

Крамеровская система – это система, удовлетворяющая следующим 2-м условиям:

1) число уравнений системы = числу неизвестных

2) определитель, составленный из коэффициентов при неизвестных, отличен от 0

Система совместима, т.е. имеет хотя бы одно решение.

2. Решить систему линейных алгебраических уравнений методом Гаусса

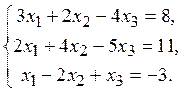
Решение:Выпишем расширенную матрицу системы

Приведем эту матрицу к ступенчатому виду. Для этого мы можем делать элементарные преобразования строк.

Т-ма Кронекери-Копелли: СЛУ совместима 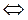, когда ранг матрицы = рангу расширенной матрицы системы.

Ранг матрицы – число ненулевых строк в ступенчатом виде матрицы

С – расширенная матрица системы, А – матрица системы

r(A)=2 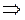r(C)=r(A) и по теореме Кронекери-Копелли система совместима. От ступенчатой матрицы переходим к ступенчатой системе:

Т. к. число уравнений системы 4 на прямую сумму подпространств размерности 2.

R 4 – множество строк длины 4 (4-х мерное арифметическое пространство)

Если А и В – подпространства пространства V, то через А+В обозначают множество

В случае, если А∩В= – нулевое подпространство, то такая сумма V=A+B называется прямой и в этом случае пишут V=A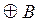. В нашем случае Ø=(0,0,0,0)

Пусть теперь А= <(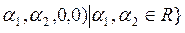B=<(0,0,

Проверим, что пространство задаётся в виде А+В

Пусть

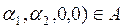
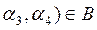
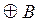
а=( в==(0,0,, значит R 4 =A.

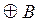
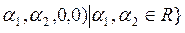
Ответ: R 4 =A, где А= <(B=<(0,0,

4. Докажите, что в пространстве M(2, R) система векторов 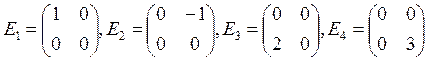линейно независима.

Система векторов а₁,а₂,а₃,а₄ линейно независима, если в любой системе вида

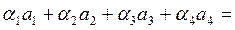
В нашем случае, пусть

Значит, система векторов Е₁, Е₂, Е₃, Е₄ линейно независима.

5. Найдите жорданову нормальную форму матриц: .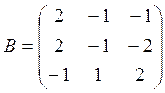

Жорданова нормальная форма матрицы состоит из клеток Жордана вдоль главной диагонали, а все остальные элементы такой матрицы нулевые.

Клетка Жордана – это матрица вида:

Если размер клетки n*n, то она обозначается символом Y_n(a).

Пример: Y₁(a)=а, Y₂(a)=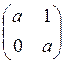, Y₃(a)=

В искомой матрице записывают характеристический многочлен матрицы А и находят его корни.

Характеристический многочлен имеет единственный корень 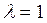кратности 3.

Надо выяснить, какой из 3-х случае нам подходит:

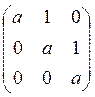
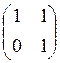
Y₁=, Y₂=, Y₃=(1)

Число всех клеток Жордана вычисляют по формуле:

A-E =

Значит, 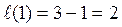. Искомая матрица имеет вид: Y=

Ответ: Y=

6. Исследовать, являются ли векторы

векторного пространства 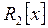линейно зависимыми.

Пусть

Это приводит к системе:

Т. к. определитель системы ≠ 0, то система имеет единственное нулевое решение. Значит, система векторов f(x), g(x), h(x) являются линейно независимыми.

Ответ: линейно независимы.

7. Найти собственные значения и собственные векторы линейного оператора пространства R 2 , заданного в некотором базисе матрицей

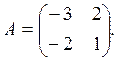
Характеристический многочлен имеет единственный корень 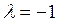кратности 2.

Значит, 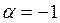— собственное значение линейного оператора.

Найдем собственный вектор, отвечающий найденному собственному значению:

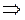
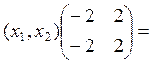
Пусть х = (х₁, х₂) х(А-

Пусть х₂=t →x₁=-t, где t – любое число

Ответ: собственное значение λ = -1, собственный вектор (-t, t), t – любое число.

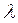
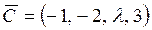
8. Найти все значения , при которых вектор линейно выражается через векторы

Мы должны найти все λ, для которых уравнение 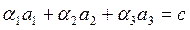(1)

имеет решение

что приводит к системе:

Уравнение (1) имеет решение ↔, когда данная система имеет решение. А согласно теореме Кронекери-Копелли данная система совместима ↔ ранг матрицы системы совпадает с рангом расширенной матрицы.