 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравненияхПрактика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
2sin x sin 2x – 2sin 2 x = 0,

Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1( · ).
Ответ:
Пример 2. tg x + tg 2x – tg 3x = 0.
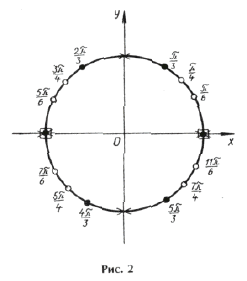
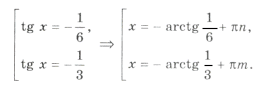
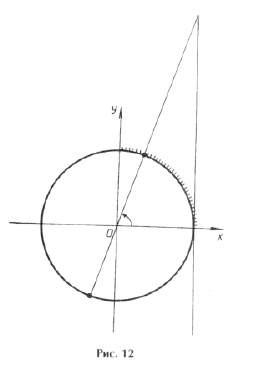
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1( o ) входит в серию x3( · ), поэтому ответ можно записать одной формулой:
Пример 3.
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
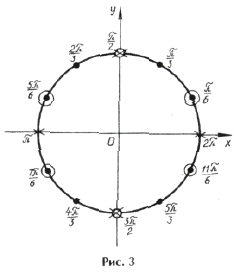
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin 2 x + sin 2 2x = sin 2 3x.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2 p ) = 0.
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
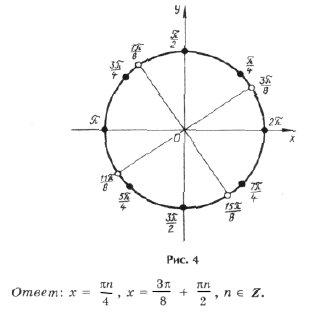
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1( · ) и x3(О), которые не совпадают.
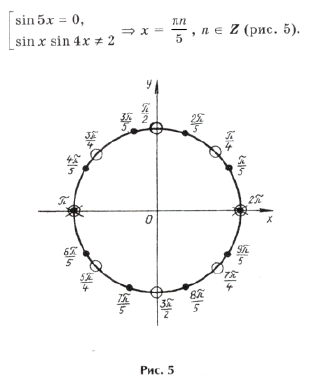
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
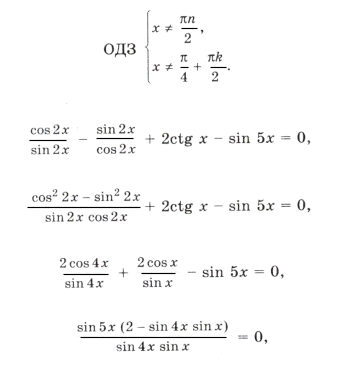
Учитывая ОДЗ, получим
Пример 7.
Иногда случается, что часть серии входит в ответ, а часть нет.
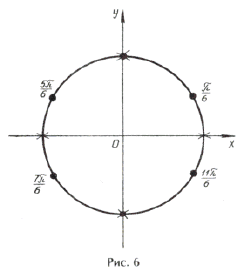
Нанесем на тригонометрический круг (рис. 6) все числа серии 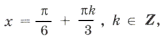
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2 p .
Пример 8. sin 2 2x + sin 2 3x + sin 2 4x + sin 2 5x = 2.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p ]. Это будут:
Сразу видно, что серия x1 содержится в серии x3, а серии x2 и x3 не пересекаются. Значит, ответ можно записать в виде .
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2 p k имеет посторонние корни, удовлетворяющие условию x № 3 p n, n О Z. Пусть p + 2 p k = 3 p n; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2 p k будет при k = 3m + 1, m О Z.
Пример 10. cos 7x (sin 5x – 1) = 0.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Ответ можно записать в виде
.
Пример 11.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Пример 12.
Решением уравнения является пересечение серий x1 и x2;
,
где
– целое число;
Пример 13.
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку
,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2 p l, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство
,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
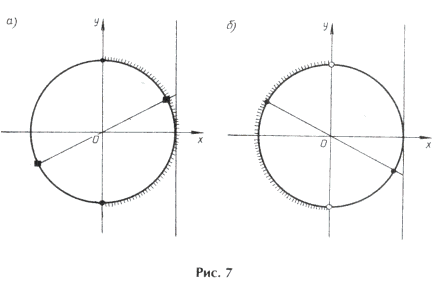
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2 p ].
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как
то
Пример 16. Найти все решения уравнения
принадлежащие отрезку
.
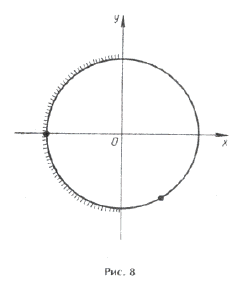
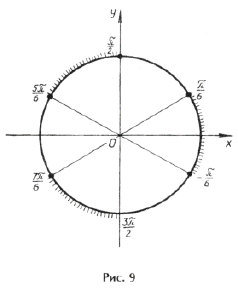
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку
принадлежит только один промежуток из ОДЗ, а именно
.
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos 2 3x Ю sin 2x = cos 6x,
Из серии
при n = 2 имеем
Из серии
при n = 5 имеем
Пример 17.
Ответ:
Пример 18. Найти все корни уравнения
которые удовлетворяют условию
.
10sin 2 x = – cos 2x + 3 Ю 10sin 2 x = 2sin 2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при
.
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут
.
Пример 19.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Ответ:
Пример 21.
а)
Но ctg x 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:

Л. Максименко,
Р. Зинченко,
г. АнгарскСодержание
- Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств
- Простейшие случаи
- Координатная прямая и числовые промежутки как объединение их частей
- Как определить пересечение и объединение при помощи изображений числовых множеств
- Операции над множествами
- Пересечение множеств
- Объединение множеств
- Решение неравенств, содержащих знак ≠
- Решение совокупностей неравенств
- 🌟 Видео
Видео:Объединение и пересечение числовых промежутков. 6 класс.Скачать
Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств
Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.
Видео:Множества. Операции над множествами. 10 класс алгебраСкачать
Простейшие случаи
Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.
Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.
Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.
Из указанных определений логически следуют следующие правила:
— чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;
— чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.
Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.
Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.
Рассмотрим применение полученных правил на практических примерах.
Исходные данные: числовые множества А = и В = . Необходимо найти объединение и пересечение исходных множеств.
Решение
- Определим объединение исходных множеств. Запишем все элементы, к примеру, множества А : 3 , 5 , 7 , 12 . Добавим к ним недостающие элементы множества В : 2 , 8 , 11 и 13 . В конечном итоге имеем числовое множество: . Упорядочим элементы полученного множества и получим искомое объединение: А ∪ B = .
- Определим пересечение исходных множеств. Согласно правилу, переберем один за другим все элементы первого множества A и проверим, входят ли они во множество B . Рассмотрим первый элемент — число 3 : он не принадлежит множеству B , а значит не будет являться элементом искомого пересечения. Проверим второй элемент множества A , т.е. число 5 : оно принадлежит множеству B , а значит станет первым элементом искомого пересечения. Третий элемент множества A – число 7 . Оно не является элементом множества B , а, следовательно, не является элементом пересечения. Рассмотрим последний элемент множества A : число 1 . Оно также принадлежит и множеству B , и соответственно станет одним из элементов пересечения. Таким образом, пересечение исходных множеств – множество, состоящее из двух элементов: 5 и 12 , т.е. А ∩ В = .
Ответ: объединение исходных множеств – А ∪ B = ; пересечение исходных множеств — А ∩ В = .
Все вышесказанное относится к работе с двумя множествами. Что же касается нахождения пересечения и объединения трех и более множеств, то решение этой задачи возможно свести к последовательному нахождению пересечения и объединения двух множеств. Например, чтобы определить пересечение трех множеств A , В и С , возможно сначала определить пересечение A и B , а затем найти пересечение полученного результата с множеством C . На примере это выглядит так: пусть будут заданы числовые множества: А = , В = и С = . Пересечение первых двух множеств составит: А ∩ В = , а пересечение полученного множества с множеством А ∩ В = . В итоге: А ∩ В ∩ С = .
Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.
Т.е., чтобы найти объединение трех и более множеств указанного типа, необходимо к элементам первого множества добавить недостающие элементы второго множества, затем – третьего и т.д. Для пояснения возьмем числовые множества: А = , В = , С = . К элементам первого множества A добавится число 3 из множества B , а затем – недостающие числа 4 и 5 множества C . Таким образом, объединение исходных множеств: А ∪ В ∪ С = .
Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:
Найдем пересечение исходных множеств. Очевидно, что множество B имеет меньше всего элементов, поэтому именно их мы будем проверять, определяя, входят ли они в остальные множества. Число 1 множества B является элементом и прочих множеств, а значит является первым элементом искомого пересечения. Второе число множества B – число 0 – не является элементом множества A , а, следовательно, не станет элементом пересечения. Продолжаем проверку: число 2 множества B является элементом прочих множеств и становится еще одной частью пересечения. Наконец, последний элемент множества B – число 12 – не является элементом множества D и не является элементом пересечения. Таким образом, получаем: A ∩ B ∩ C ∩ D = .
Видео:Пересечение множеств. Объединение множеств. 5 класс.Скачать
Координатная прямая и числовые промежутки как объединение их частей
Отметим на координатной прямой произвольную точку, например, с координатой — 5 , 4 . Указанная точка разобьет координатную прямую на два числовых промежутка – два открытых луча (-∞, -5,4) и (-5,4, +∞) и собственно точку. Нетрудно увидеть, что в соответствии с определением объединения множеств любое действительное число будет принадлежать объединению ( — ∞ , — 5 , 4 ) ∪ ∪ ( — 5 , 4 , + ∞ ) . Т.е. множество всех действительных чисел R = ( — ∞ ; + ∞ ) возможно представить в виде полученного выше объединения. И наоборот, полученное объединение будет являться множеством всех действительных чисел.
Отметим, что заданную точку возможно присоединить к любому из открытых лучей, тогда он станет простым числовым лучом ( — ∞ , — 5 , 4 ] или [ — 5 , 4 , + ∞ ) . При этом множество R будет описываться следующими объединениями: ( — ∞ , — 5 , 4 ] ∪ ( — 5 , 4 , + ∞ ) или ( — ∞ , — 5 , 4 ) ∪ [ — 5 , 4 , + ∞ ) . .
Подобные рассуждения действительны не только относительно точки координатной прямой, но и относительно точки на любом числовом промежутке. Т.е., если мы возьмем любую внутреннюю точку любого произвольного промежутка, его возможно будет представить, как объединение его частей, полученных после деления заданной точкой, и самой точки. К примеру, задан полуинтервал ( 7 , 32 ] и точка 13 , принадлежащая этому числовому промежутку. Тогда заданный полуинтервал можно представить в виде объединения ( 7 , 13 ) ∪ ∪ ( 13 , 32 ] и обратно. Мы можем включить число 13 в любой из промежутков и тогда заданное множество ( 7 , 32 ] можно представить, как ( 7 , 13 ] ∪ ( 13 , 32 ] или ( 7 , 13 ] ∪ ( 13 , 32 ] . Также мы можем взять в качестве исходных данных не внутреннюю точку заданного полуинтервала, а его конец (точку с координатой 32 ), тогда заданный полуинтервал можно представить, как объединение интервала ( 7 , 32 ) и множества из одного элемента . Таким образом: ( 7 , 32 ] = ( 7 , 32 ) ∪ .
Еще один вариант: когда берется не одна, а несколько точек на координатной прямой или числовом промежутке. Эти точки разобьют координатную прямую или числовой промежуток на несколько числовых промежутков, а объединение этих промежутков будут составлять исходные множества. К примеру, на координатной прямой заданы точки с координатами — 6 , 0 , 8 , которые разобьют ее на промежутки: ( — ∞ , — 6 ) , ( — 6 , 0 ) , ( 0 , 8 ) , ( 8 , + ∞ ) . При этом множество всех действительных чисел, олицетворением чего и является координатная прямая, возможно представить в виде объединения полученных промежутков и указанных чисел:
( — ∞ , — 6 ) ∪ ∪ ( — 6 , 0 ) ∪ ∪ ( 0 , 8 ) ∪ ∪ ( 8 , + ∞ ) .
Видео:Множества и операции над нимиСкачать
Как определить пересечение и объединение при помощи изображений числовых множеств
С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).
Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.
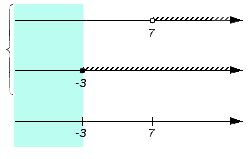
Исходные данные: заданы числовые множества А = ( 7 , + ∞ ) и В = [ — 3 , + ∞ ) . Необходимо найти пересечение и объединение данных множеств.
Решение
- Изобразим заданные числовые множества на координатных прямых. Их необходимо расположить друг над другом. Для удобства принято считать, что точки начала отсчета заданных множеств совпадают, и остается сохранным расположение точек друг относительно друга: любая точка с большей координатой лежит правее точки с меньшей координатой. При этом, если нам интересно объединение множеств, то координатные прямые объединяют слева квадратной скобкой совокупности; если интересует пересечение, то – фигурной скобкой системы.
В нашем примере для записи пересечения и объединения числовых множеств имеем:
и
Изобразим еще одну координатную прямую, расположив ее под уже имеющимися. Она понадобится для отображения искомого пересечения или объединения. На этой координатной прямой отмечают все граничные точки исходных числовых множеств: сначала черточками, а позже, после выяснения характера точек с этими координатами, черточки будет заменены выколотыми или невыколотыми точками. В нашем примере это точки с координатами — 3 и 7 .
и
Точки, которые изображены на нижней координатной прямой в предыдущем шаге алгоритма, дают возможность рассматривать координатную прямую как набор числовых промежутков и точек (об этом мы говорили выше). В нашем примере координатную прямую представим в виде набора пяти числовых множеств: ( — ∞ , — 3 ) , , ( — 3 , 7 ) , , ( 7 , + ∞ ) .
Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:
-. промежуток становится частью пересечения, если он одновременно является частью множества A и множества B (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества А и B );
— точка становится частью пересечения, если она является одновременно частью каждого из множеств А и В (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств A и B );
— промежуток становится частью объединения, если он является частью хотя бы одного из множеств A или B (иными словами – если присутствует штриховка над этим промежутком хотя бы на одной из координатных прямых, отображающих множества A и B .
— точка становится частью объединения, если она является частью хотя бы одного из множеств A и B (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств A и B ).
Кратко резюмируя: пересечением числовых множеств A и B служит пересечение всех числовых промежутков множеств A и B , над которыми одновременно присутствует штриховка, и всех отдельных точек, принадлежащих и множеству А, и множеству В. Объединением числовых множеств A и B служит объединение всех числовых промежутков, над которыми присутствует штриховка хотя бы у одного из множеств A или B , а также всех невыколотых отдельных точек.
- Вернемся к примеру, определим пересечение заданных множеств. Для этого поочередно проверим множества: ( — ∞ , — 3 ) , , ( — 3 , 7 ) , , ( 7 , + ∞ ) . Начнем с множества ( — ∞ , — 3 ) , наглядно выделив его на чертеже:
Этот промежуток не будет включен в пересечение, потому что не является частью ни множества A , ни множества B (нет штриховки). И так наш чертеж сохраняет свой изначальный вид:
Рассмотрим следующее множество . Число — 3 является частью множества B (невыколотой точкой), но не входит в состав множества A , а потому не станет частью искомого пересечения. Соответственно на нижней координатной прямой точку с координатой — 3 делаем выколотой:
Оцениваем следующее множество ( — 3 , 7 ) .
Оно является частью множества B (над интервалом присутствует штриховка), но не входит в множество A (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:
Следующее множество на проверку — . Оно является составом множества B (точка с координатой 7 является внутренней точкой промежутка [ — 3 , + ∞ ) ), но не является частью множества A (выколотая точка), таким образом, рассматриваемый промежуток не станет частью искомого пересечения.. Отметим точку с координатой 7 как выколотую:
И, наконец, проверяем оставшийся промежуток ( 7 , + ∞ ) .
Промежуток входит в оба множества A и B (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:
В конечном счете на нижней координатной прямой образовалось изображение искомого пересечения заданных множеств. Очевидно, что оно является множеством всех действительных чисел больше числа 7 , т.е.: А ∩ В = ( 7 , + ∞ ) .
- Следующим шагом определим объединение заданных множеств A и B . Последовательно проверим множества ( — ∞ , — 3 ) , , ( — 3 , 7 ) , , ( 7 , + ∞ ) , устанавливая факт включения или невключения их в искомое объединение.
Первое множество ( — ∞ , — 3 ) не является частью ни одного из исходных множеств A и B (над промежутками нет штриховок), следовательно, множество ( — ∞ , — 3 ) не войдет в искомое объединение:
Множество входит в множество B , а значит будет входить в искомое объединение множеств A и B :
Множество ( — 3 , 7 ) является составной частью множества B (над интервалом присутствует штриховка) и становится элементом объединения множеств A и B :
Множество 7 входит в числовое множество B , поэтому войдет и в искомое объединение:
Множество ( 7 , + ∞ ) , являясь элементом обоих множеств А и В одновременно, становится еще одной частью искомого объединения:
По итоговому изображению объединения исходных множеств А и В получаем: А ∩ В = [ — 3 , + ∞ ) .
Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.
Исходные данные: множества А = ( — ∞ , — 15 ) ∪ ∪ [ 0 , 7 ) ∪ и В = ( — 20 , — 10 ) ∪ ∪ ( 2 , 3 ) ∪ . Необходимо определить пересечение и объединение заданных множеств.
Решение
Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:
Ответ: А ∩ В = ( — 20 , — 15 ) ∪ ∪ ( 2 , 3 ) ; А ∪ В = ( — ∞ , — 10 ) ∪ ∪ [ 0 , 7 ] ∪ .
Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.
Исходные данные: множества А = ∪ [ 1 , 5 ] и B = [ — 4 , 3 ] .
Необходимо определить пересечение исходных множеств.
Решение
Геометрически изобразим числовые множества А и В :
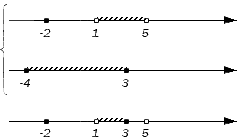
Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:
( — ∞ , — 4 ) , , ( — 4 , — 2 ) , , ( — 2 , — 1 ) , , ( 1 , 3 ) , , ( 3 , 5 ) , , ( 5 , + ∞ ) .
Легко заметить, что числовое множество A можно записать, объединив некоторые из перечисленных множеств, а именно: , ( 1 , 3 ) , и ( 3 , 5 ) . Достаточно будет проверить эти множества на их включенность также в множество В для того, чтобы найти искомое пересечение. Те, что войдут в множество В и станут элементами пересечения. Проведем проверку.
Совершенно понятно, что является частью множества B , ведь точка с координатой — 2 – внутренняя точка отрезка [ — 4 , 3 ) . Интервал ( 1 , 3 ) и множество также входят в множество В (над интервалом присутствует штриховка, а точка с координатой 3 является для множества В граничной и невыколотой). Множество ( 3 , 5 ) не будет элементом пересечения, т.к. не входит в множество В (над ним не присутствует штриховка). Отметим все вышесказанное на чертеже:
В итоге искомым пересечением двух заданных множеств будет объединение множеств, которое мы запишем так: ∪ ( 1 , 3 ] .
Ответ: А ∩ В = ∪ ( 1 , 3 ] .
В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более 2 ). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.
Исходные данные: множества А = ( — ∞ , 12 ] , В = ( — 3 , 25 ] , D = ( — ∞ , 25 ) ꓴ . Необходимо определить пересечение и объединение заданных множеств.
Решение
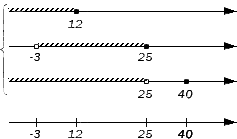
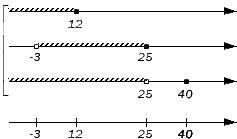
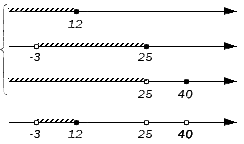
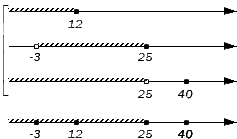
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:
Таким образом, координатная прямая представлена следующими множествами: ( — ∞ , — 3 ) , , ( — 3 , 12 ) , , ( 12 , 25 ) , , ( 25 , 40 ) , , ( 40 , + ∞ ) .
Начинаем искать пересечения, поочередно проверяя записанные множества на принадлежность каждому из исходных. Во все три заданных множества входит интервал ( — 3 , 12 ) и множество : они и станут элементами искомого пересечения. Таким образом, получим: A ∩ B ∩ D = ( — 3 , 12 ] .
Объединение заданных множеств составят множества: ( — ∞ , — 3 ) — элемент множества А ; – элемент множества А ; ( — 3 , 12 ) – элемент множества А ; – элемент множества А ; ( 12 , 25 ) – элемент множества В ; – элемент множества В и – элемент множества D . Таким образом, получим: A ∪ B ∪ D = ( — ∞ , 25 ] ∪ .
Ответ: A ∩ B ∩ D = ( — 3 , 12 ] ; A ∪ B ∪ D = ( — ∞ , 25 ] ∪ .
Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.
Исходные данные: А = [ — 7 , 7 ] ; В = ∪ [ — 12 , 0 ) ∪ ; D = [ — 15 , — 10 ] ∪ [ 10 , + ∞ ) ; Е = ( 0 , 27 ) . Определить пересечение заданных множеств.
Решение
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.
Отмеченные точки разобьют числовую прямую на множества: ( — ∞ , — 15 ) , , ( — 15 , — 12 ) , , ( — 12 , — 10 ) , , ( — 10 , — 7 ) , , ( — 7 , 0 ) , , ( 0 , 5 ) , , ( 5 , 7 ) , , ( 7 , 10 ) , , ( 10 , 27 ) , , ( 27 , + ∞ ) .
Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.
Ответ: A ∩ B ∩ D ∩ Е = Ø .
Множества удобно изображать в виде кругов, которые называют кругами Эйлера.
На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.
Видео:Пересечение и объединение множеств. Алгебра, 8 классСкачать
Операции над множествами
Видео:6 класс, 4 урок, Множество. Объединение и пересечение множествСкачать
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
Друзья Джона = < Том,
Фред,
Макс,
Джорж >
Друзья Майкла = < Лео,
Том,
Фред,
Эван >Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
Общие друзья Джона и Майкла = В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A , множество друзей Майкла — через букву B , а множество общих друзей Джона и Майкла обозначим через букву C :
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A , а множество друзей Майкла через букву B
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Пример 2. Рассмотрим два множества: множество A , состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B , состоящее из чисел 1, 4, 5, 7
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B.
Пример 4. Найти пересечение следующих множеств:
Пересечением множеств A , B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A , B и C . Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5 . Пересечением в данном случае является множество, состоящее из элементов 3 и 5 . Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8] . Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6] , так и второму [4; 8] .
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6] , на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6] , принадлежат как промежутку [2; 6] , так и промежутку [4; 8] . Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6] . В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле, что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента . Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента , на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества и числового промежутка (−3; 4) будет множество, состоящее из одного элемента , поскольку элемент 2 принадлежит как множеству , так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств
, мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы
на координатной прямой, то увидим, что эти решения принадлежат промежутку [3; 6] , который в свою очередь является пересечением промежутков [3; +∞) и (−∞; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
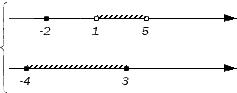
Решением первого неравенства является числовой промежуток (−∞; −1) .
Решением второго неравенства является числовой промежуток (−∞; −5) .
Решением третьего неравенства является числовой промежуток (−∞; 4) .
Решением системы
будет пересечение числовых промежутков (−∞; −1), (−∞; −5) и (−∞; 4) . В данном случае этим пересечением является промежуток (−∞; −5) .
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5) , одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе
с помощью числового промежутка:
Пример 3. Решить неравенство
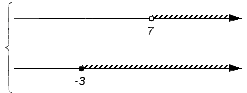
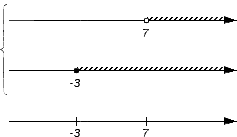
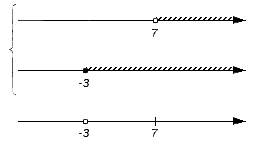
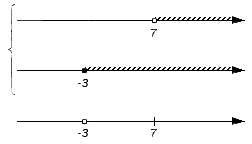
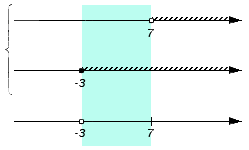
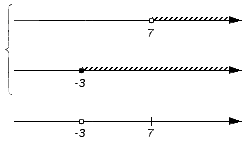
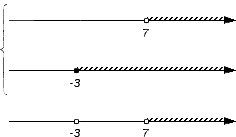
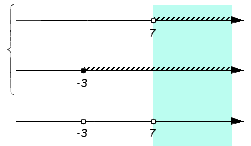
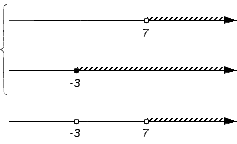
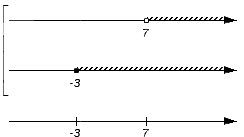
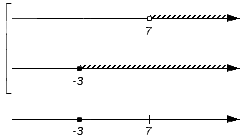
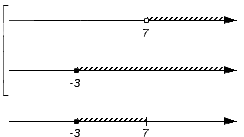
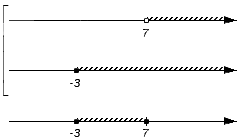
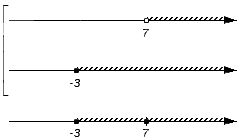
Решением первого неравенства y > 7 является числовой промежуток (7; +∞) .
Решением второго неравенства y является числовой промежуток (−∞; 4) .
Решением системы
будет пересечение числовых промежутков (7; +∞) и (−∞; 4) .
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Видео:Пример 51. Найти числовые множества (алгебра 9 класс)Скачать
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C , куда входят все элементы множеств A и B . Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Если 5 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Возьмем ещё один элемент из множества С , например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A , и множеству B . Если мы захотим объединить множества A и B , то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B .
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Теперь добавим элементы из множества B , которые не принадлежат множеству A . Множеству A не принадлежат элементы 5 и 6 . Их и добавим во множество C
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
Друзья Джона = < Том,
Фред,
Макс,
Джорж >
Друзья Майкла = < Лео,
Том,
Фред,
Эван >Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
Все друзья Джона и Майкла = В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5] . Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1 , 0 ∈ [−7; 0]
−3,−2, −1 , 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
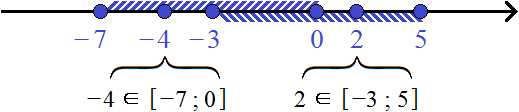
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5] , который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5] . На верхней области отметим числовой промежуток [−7; 0] , на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] . Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5] , то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5] .
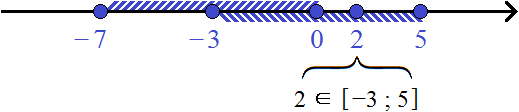
Возьмём из промежутка [−7; 5] любое число, например число 2 . Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] , то число 2 будет принадлежать хотя бы одному из этих промежутков. В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4 . Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5] . В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2 . Оно принадлежит как промежутку [−7; 0] , так и промежутку [−3; 5] . Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2 ;−1] и [4 ; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7] . Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
Получили множество . Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4 , не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15] , поскольку она не содержит все числа, которые должна была содержать.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8 . Чтобы решить такое неравенство, нужно найти множество значений переменной x , при которых левая часть не равна правой части.
Решим неравенство 2x ≠ 8 . Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4 . Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8 , то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8 . Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8 .
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞) . Напомним, что для слова «или» используется символ ∪
В этом выражении говорится, что значения, принимаемые переменной x , принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠ , также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак = . Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8 , как обычное уравнение. Заменим знак ≠ на знак равенства = , получим уравнение 2x = 8 . Разделим обе части данного уравнения на 2 , получим x = 4 .
Видим, что при x , равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2 .
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞) . Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6] .
Множество значений x , при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6] . Так и записываем:
В этом выражении говорится, что переменная x , входящая в
совокупностьпринимает все значения, принадлежащие промежутку [3; +∞) или промежутку (−∞; 6] . А это то, что нам нужно. Ведь решить совокупность означает найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность. А любое число из промежутка [3; +∞) или промежутка (−∞; 6] будет удовлетворять хотя бы одному неравенству.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6] . Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности
будет объединение числовых промежутков [3; +∞) и (−∞; 6]
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞) . Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Возьмем еще какое-нибудь число, например, число 5 . Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x . Этим множеством является числовой промежуток (−∞; −0,25) .
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств
будет объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности
будет объединение числовых промежутков (−∞; −0,25) и [−7; +∞)
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
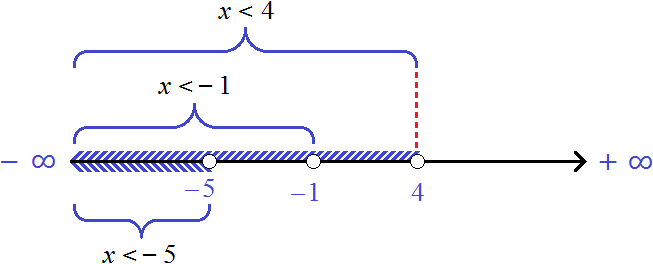
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x является числовой промежуток (−∞; −3) .
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0] .
Решением совокупности неравенств
будет объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности
будет объединение числовых промежутков (−∞; −3) и (−∞; 0]
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
🌟 Видео
Учебник 6кл.Тема: Разность двух конечных множеств.Скачать
Разность множествСкачать
Алгебра 8 класс (Урок№39 - Пересечение и объединение множеств.)Скачать
Операции над множествамиСкачать
Пересечение и объединение множеств.Решение примеровСкачать
9 класс, 2 урок, Множества и операции над нимиСкачать
A.2.9 Пересечение, объединение и симметрическая разность множествСкачать
СЛОЖИТЕ ДВА КОРНЯСкачать
Пересечение множеств. Объединение множеств. Практическая часть. 5 класс.Скачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
Числовые Промежутки — Алгебра 8 класс / Подготовка к ЕГЭ по МатематикеСкачать
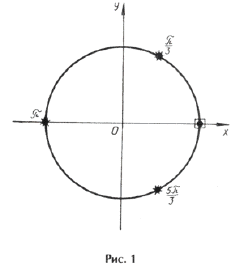
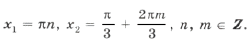
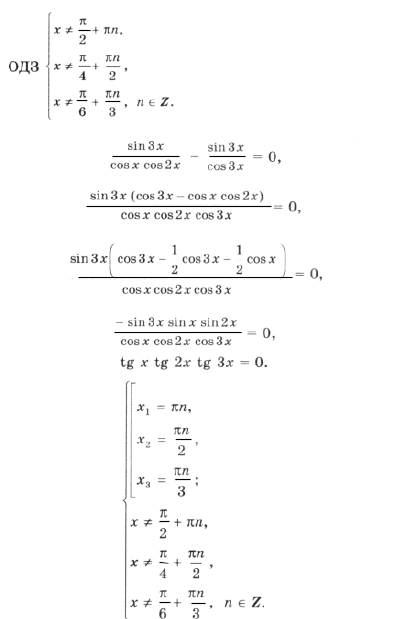
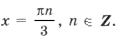
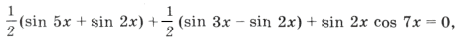
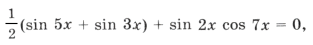
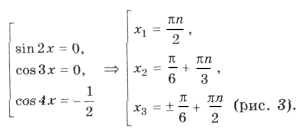
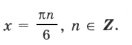
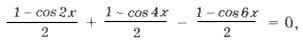
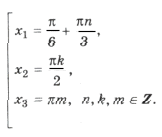
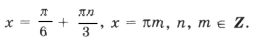
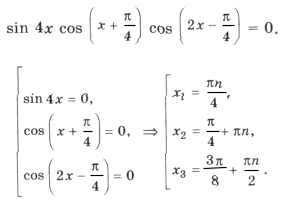
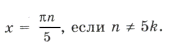
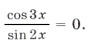
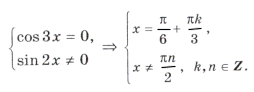
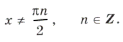
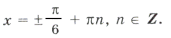
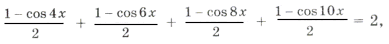
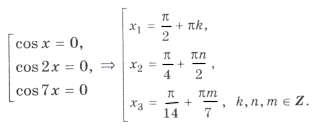
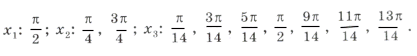
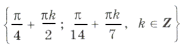
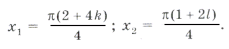
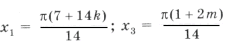
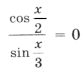
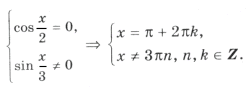
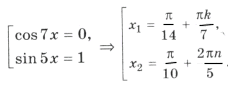
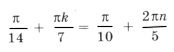
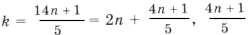 – целое число.
– целое число.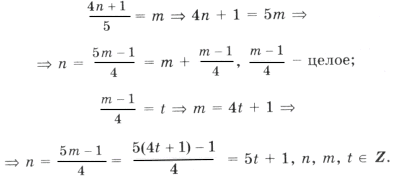
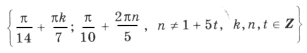 .
.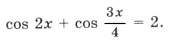
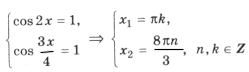
 ,
,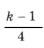 – целое число;
– целое число;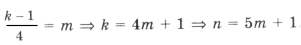
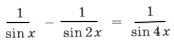
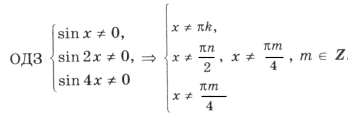
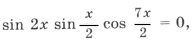
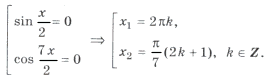
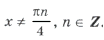
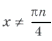 ,
,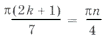 ,
,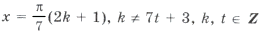
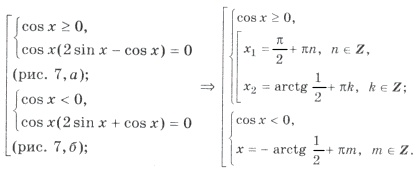

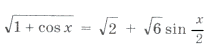
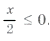
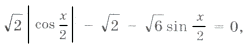
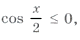 то
то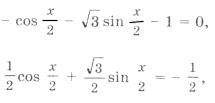
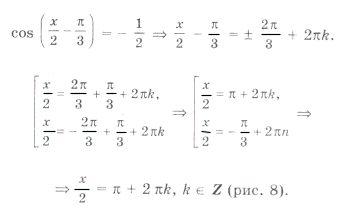
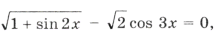
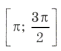 .
.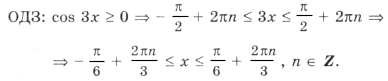
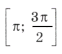 принадлежит только один промежуток из ОДЗ, а именно
принадлежит только один промежуток из ОДЗ, а именно 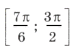 .
.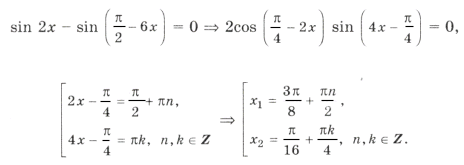
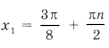 при n = 2 имеем
при n = 2 имеем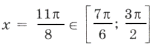
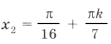 при n = 5 имеем
при n = 5 имеем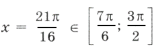
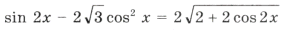
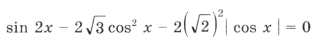
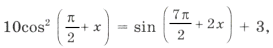
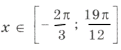 .
.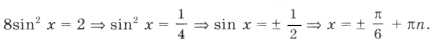
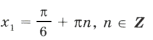
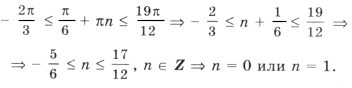
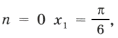
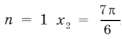 .
.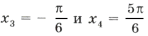 .
.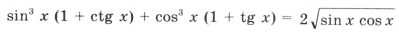
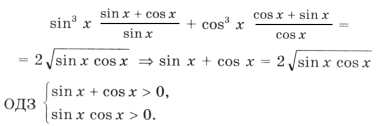
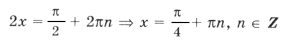
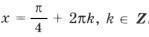
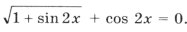
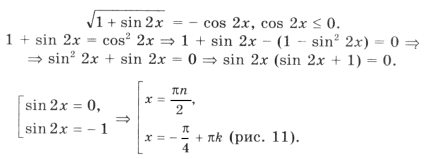
 .
.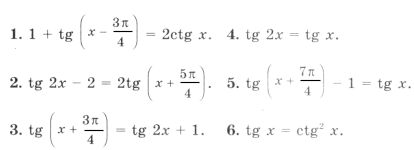
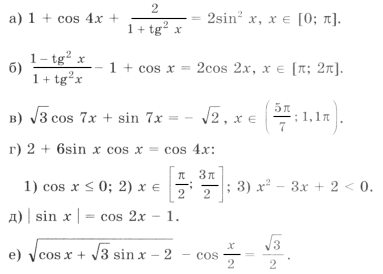





 и
и 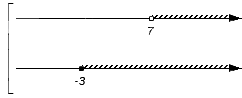
 и
и 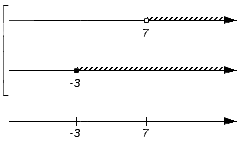


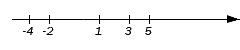






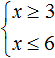 , мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.
, мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.

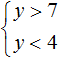







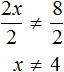

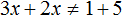
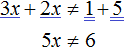
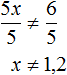


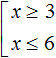
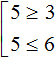
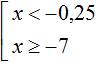

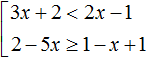
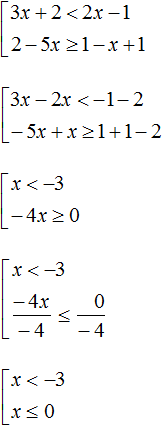
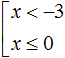 будет объединение множеств решений первого и второго неравенства.
будет объединение множеств решений первого и второго неравенства.










